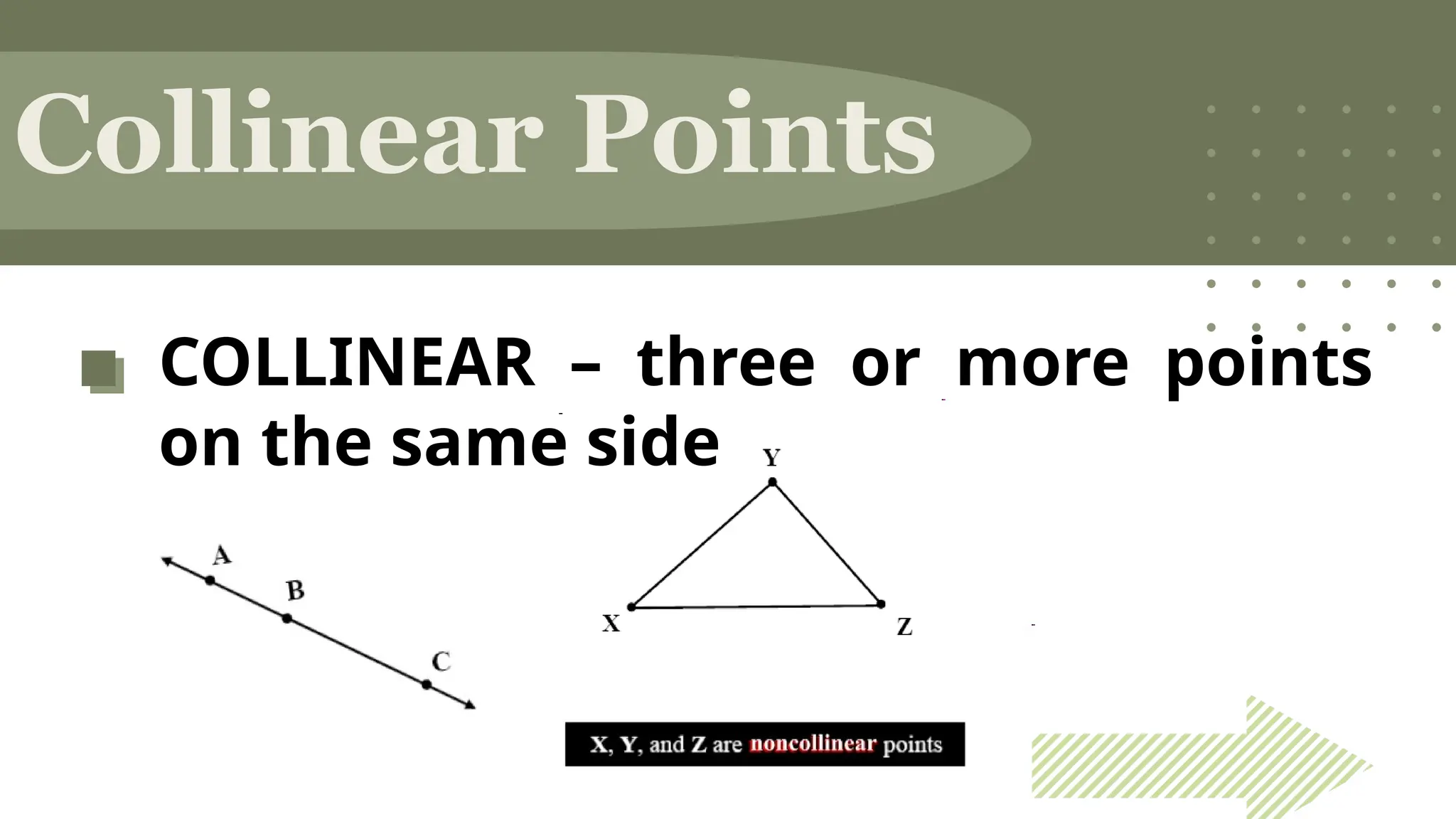
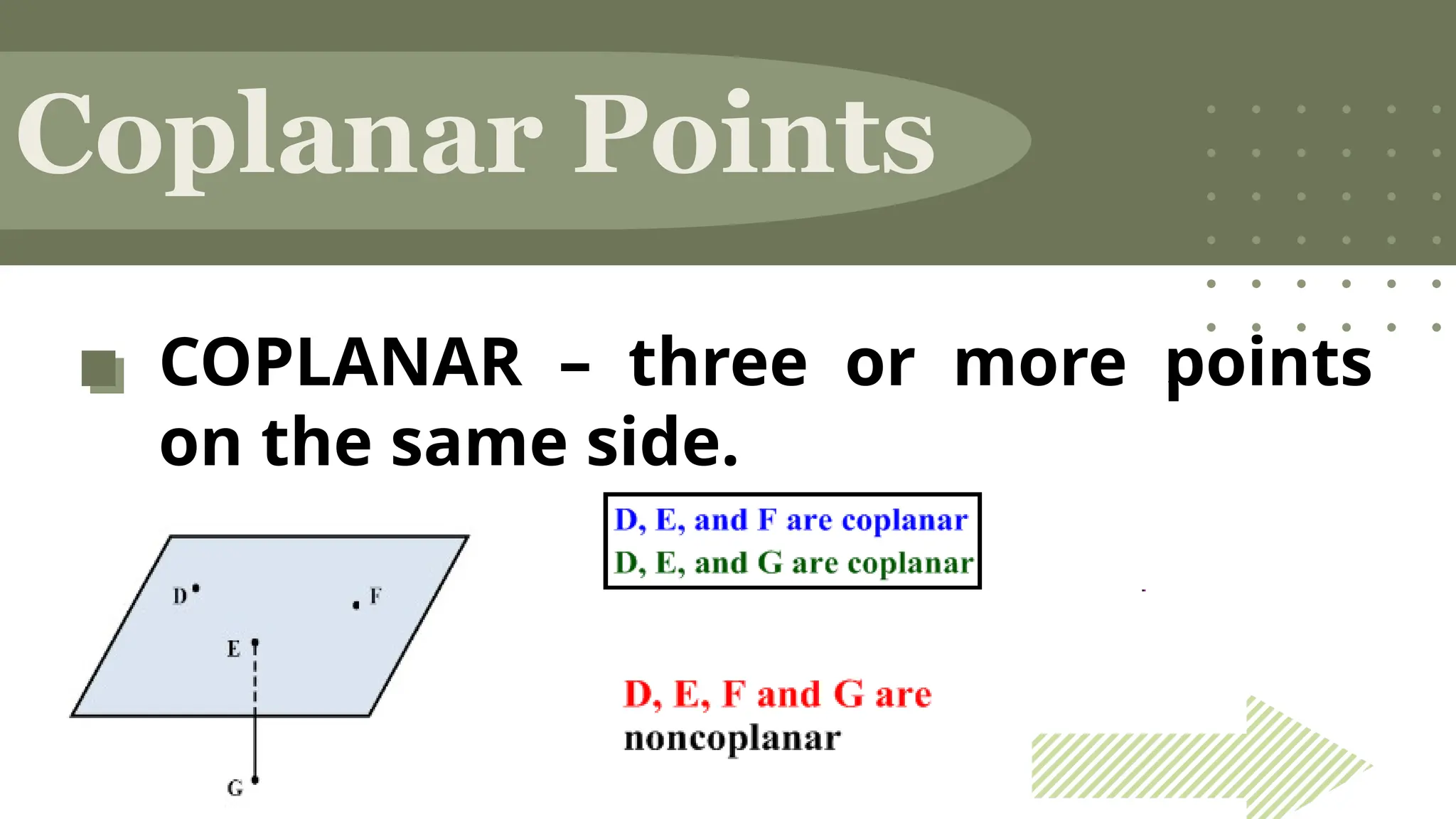
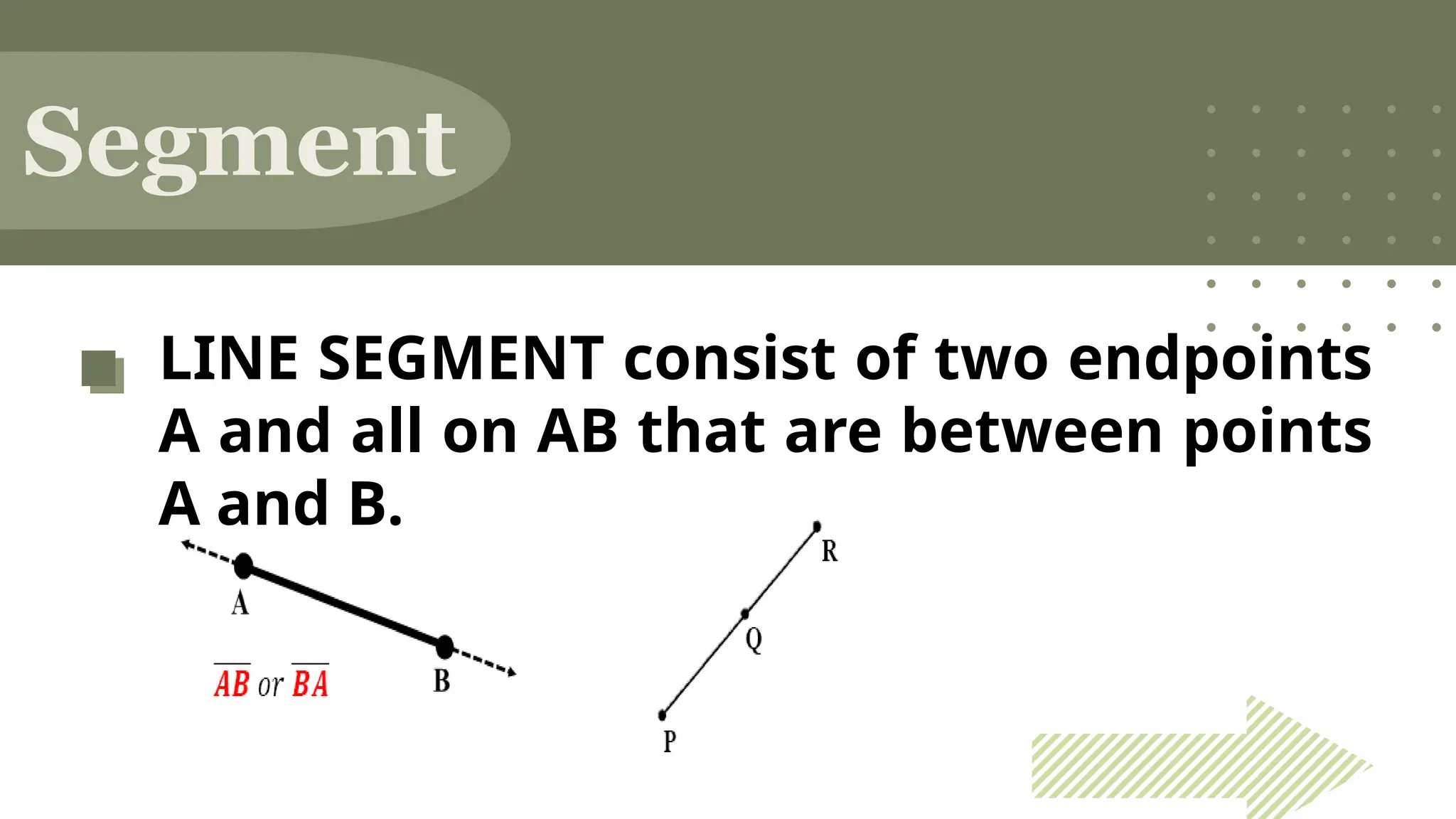
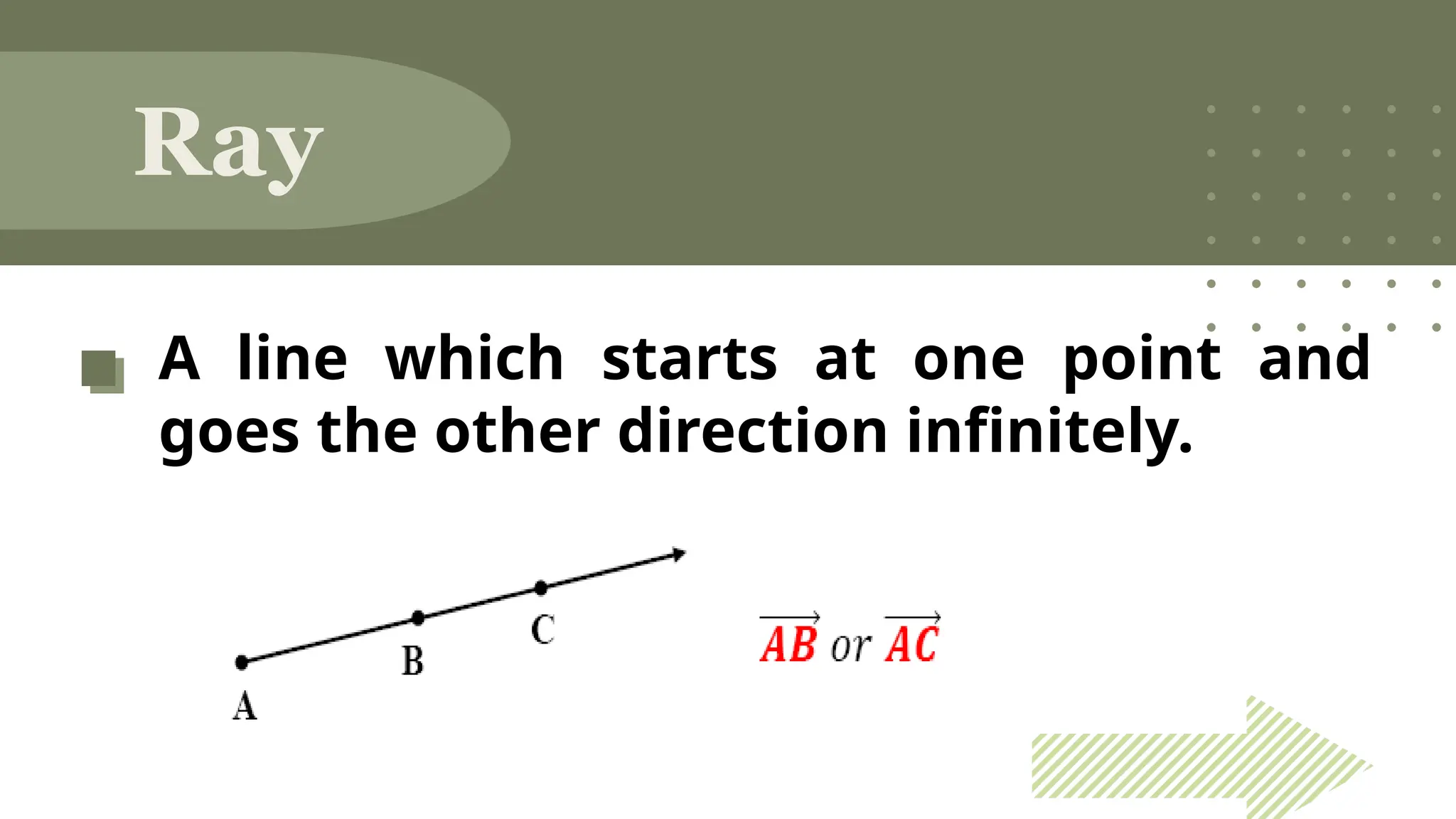
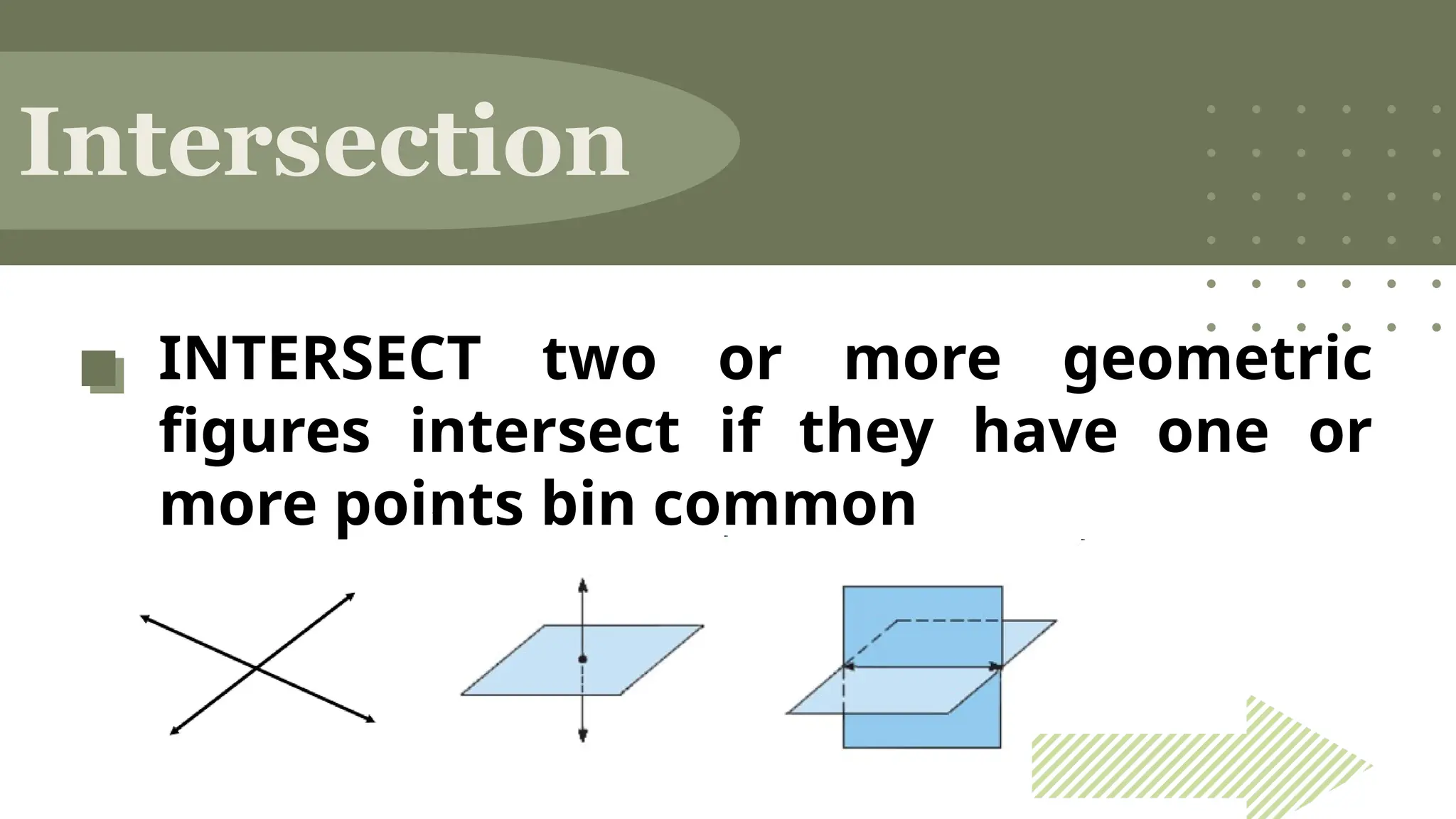
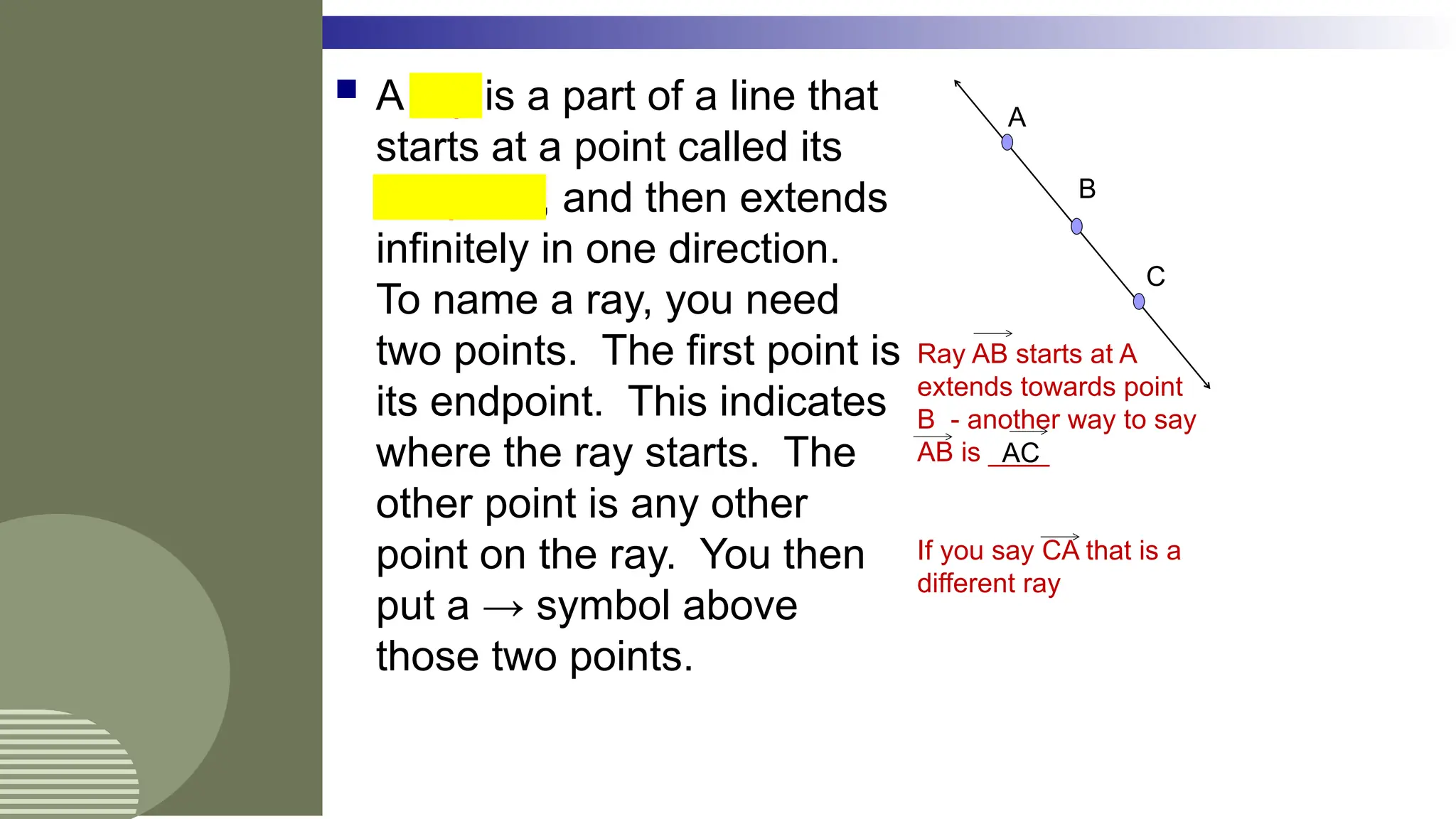
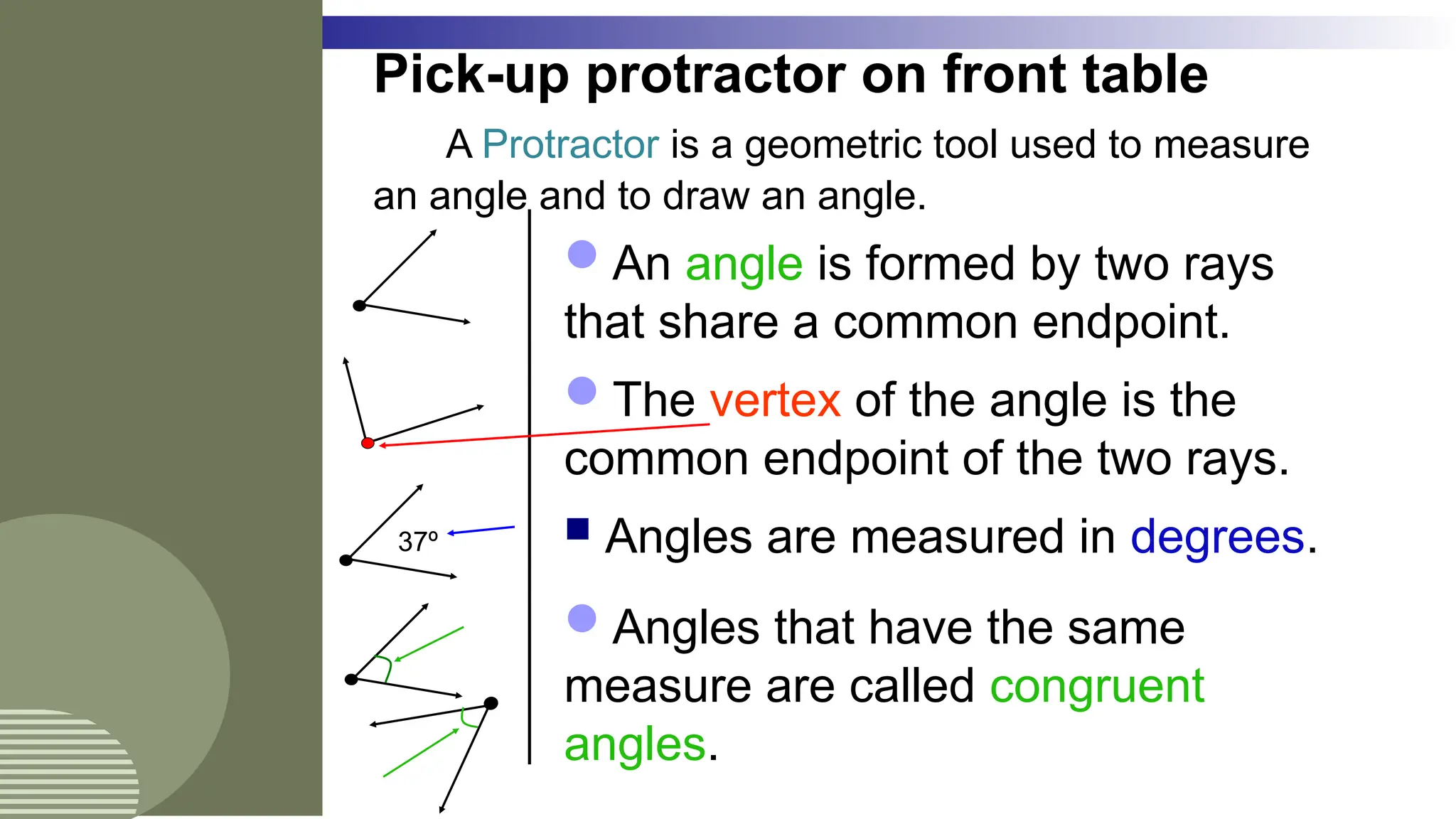
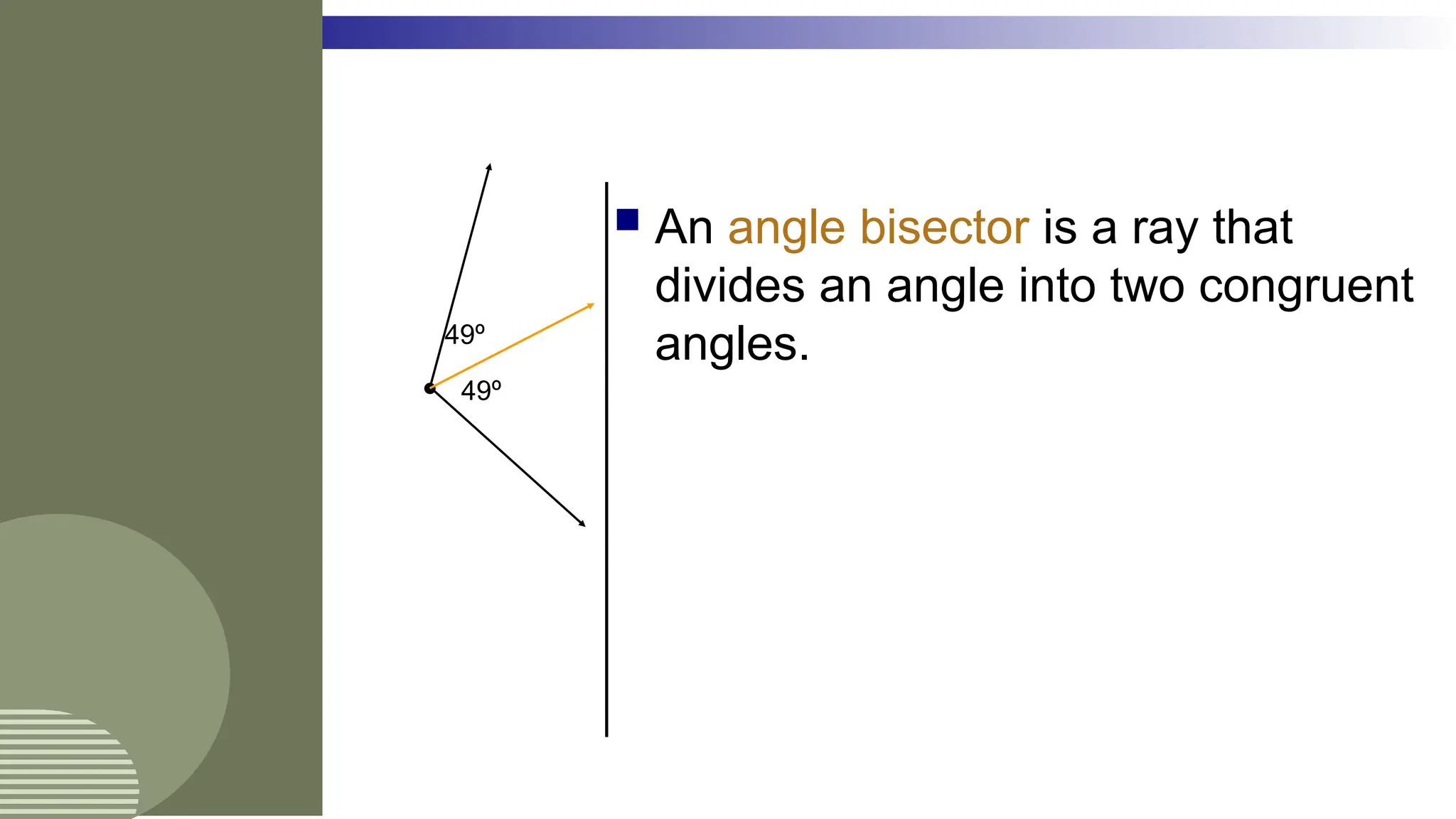
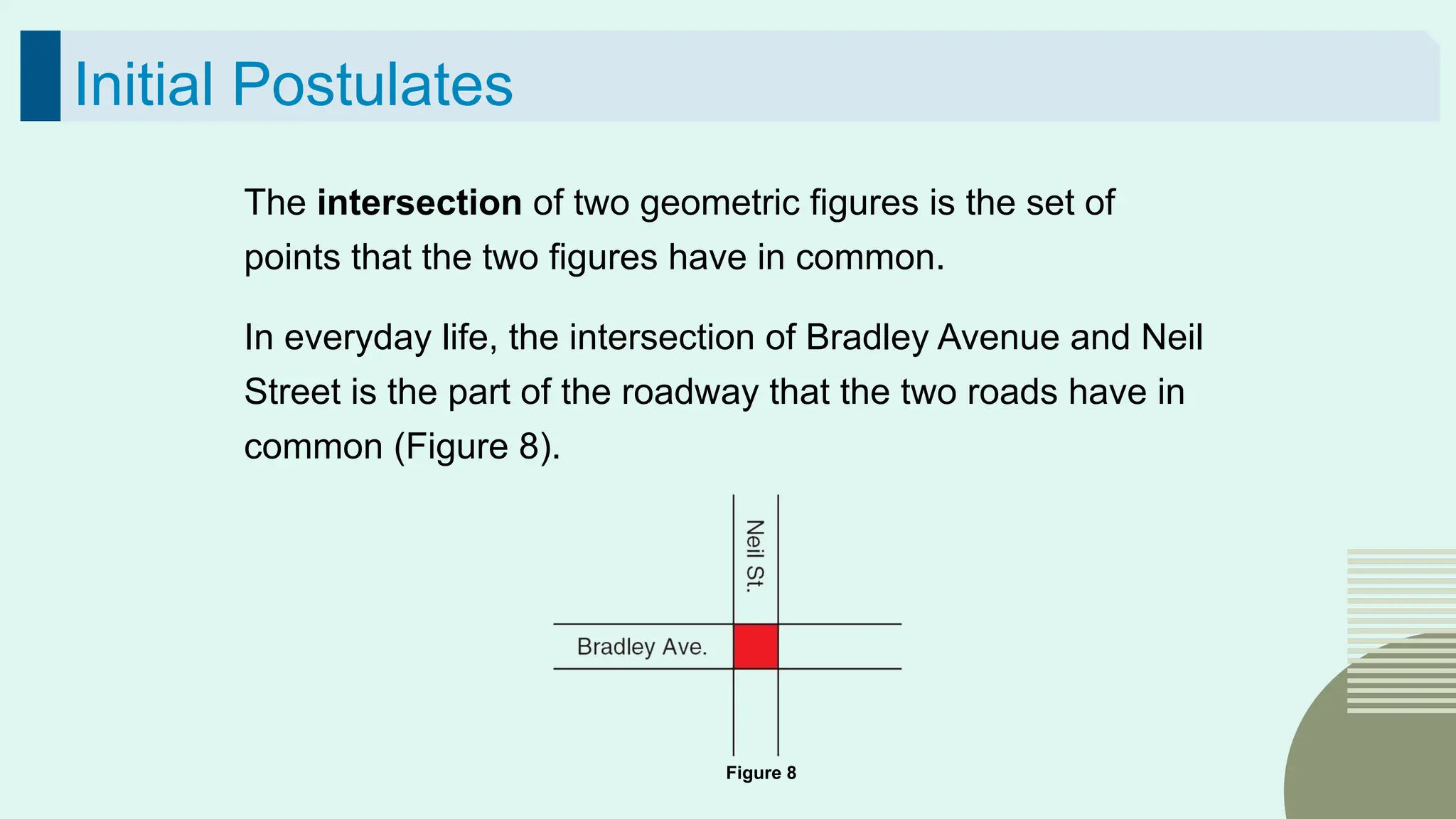
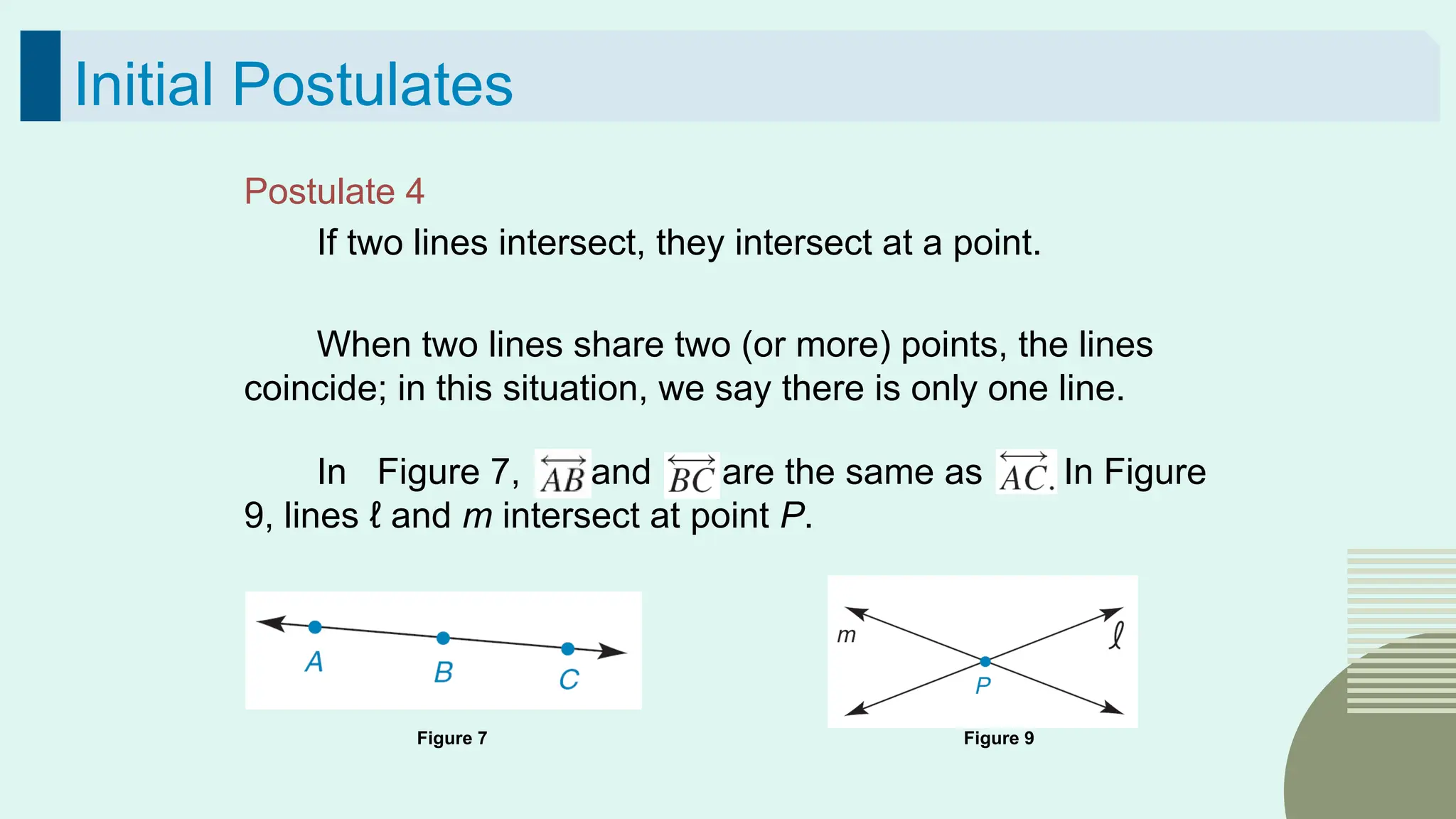
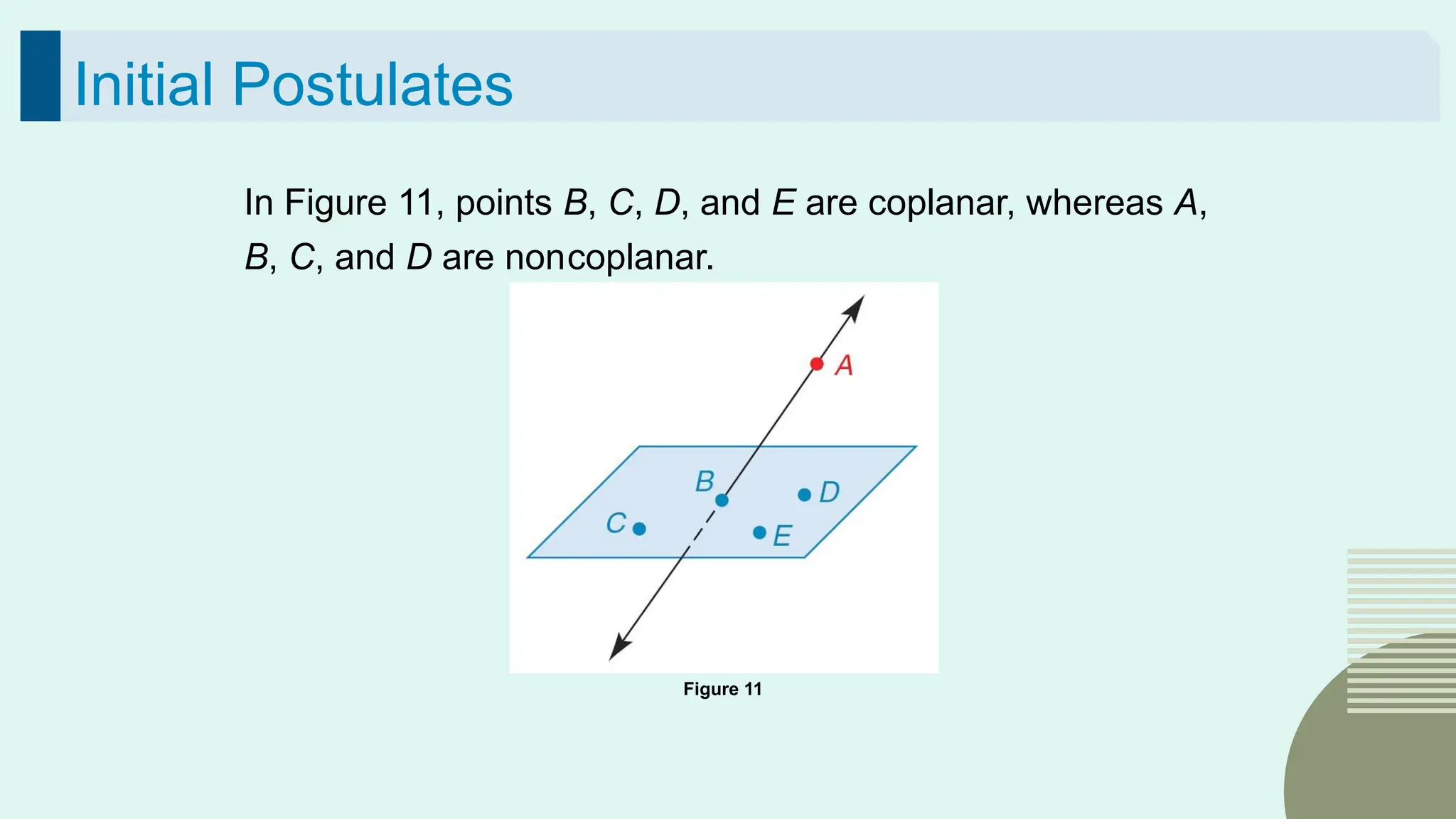
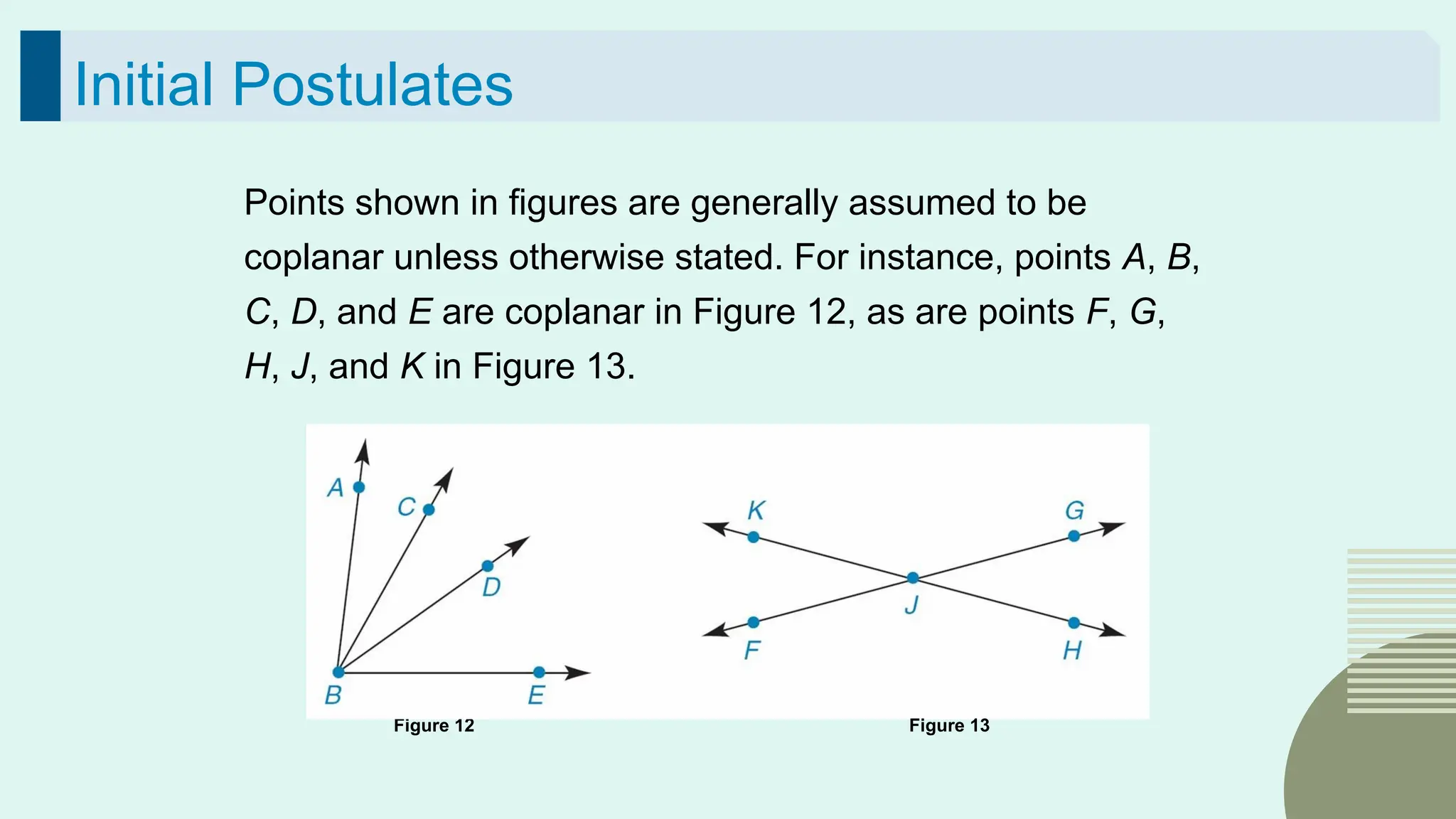
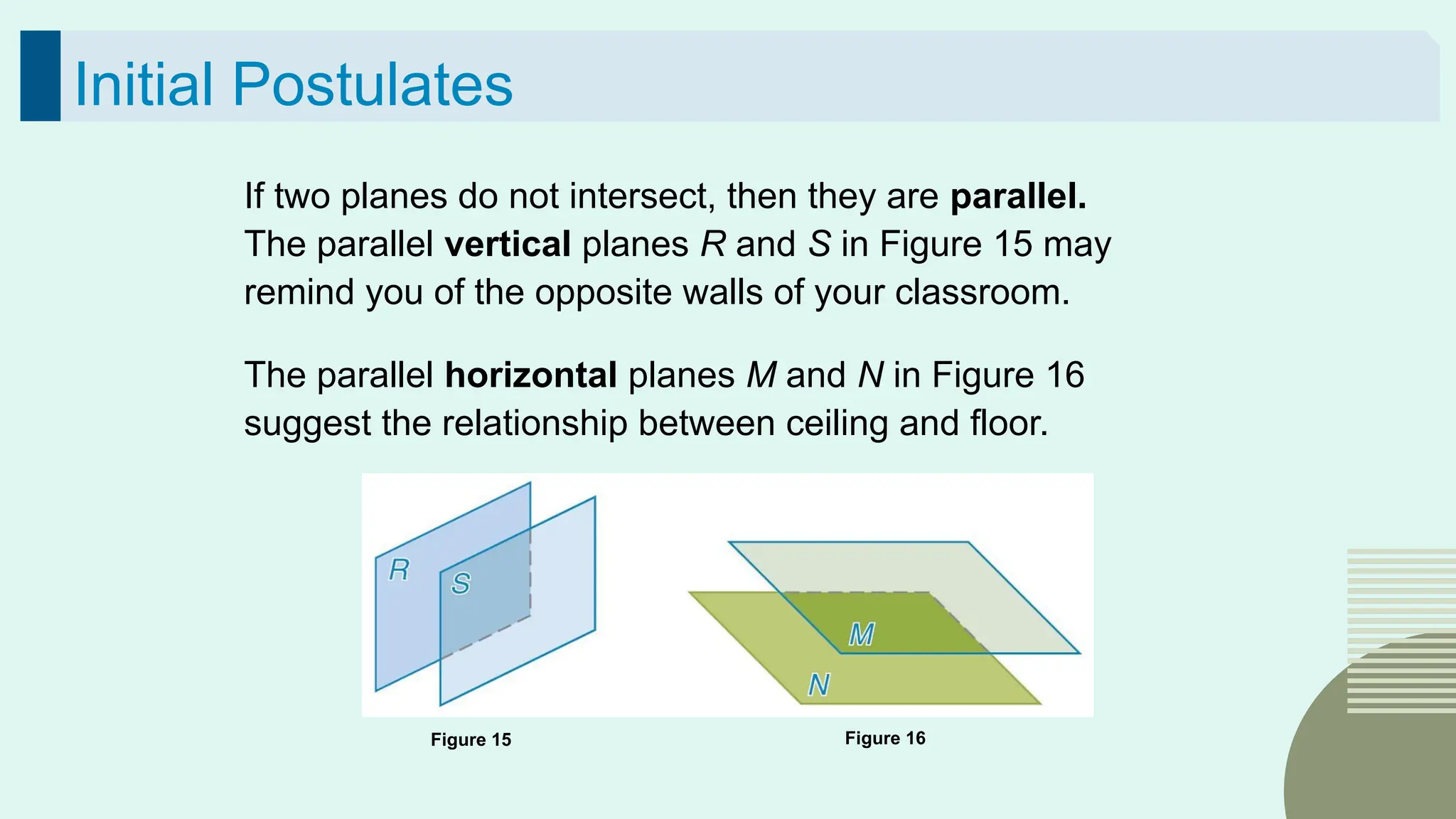
The document outlines the foundational concepts of geometry as a mathematical system, emphasizing the importance of axioms, undefined and defined terms, and theorems. It discusses key geometric elements, including points, lines, segments, and planes, while introducing concepts like collinearity, coplanarity, and the properties of geometric figures. Additionally, it details various postulates that govern geometric relationships and the deductive reasoning process used in geometry.

1. Measurement
System

2. Learning Outcomes
Describes a mathematical system. (M8GE-IIIa-1)
Illustrates the need for an axiomatic structure of a
mathematical system in general, and in Geometry in
particular: (a) defined terms; (b) undefined terms; (c)
postulates; and (d) theorems. (M8GE-IIIa-c-1)

3. EOGETRYM
GEOMET
RY

4. EUCLID’S GEOMETRY
GEOMETRY
GEO METRE
Earth To measure
Geometry originated in Egypt as an art of Earth measurement
Euclid (325 BCE-265 BCE):The Father of Geometry
The first Egyptian mathematician who initiated a new way of thinking
the study of geometry. Introduced the method of proving a geometrical
result by deductive reasoning based upon previously proved result &
some self-evident specific assumptions called axioms.

5. A Mathematical
System
Like algebra, the branch of mathematics called geometry is a
mathematical system.
The formal study of a mathematical system begins with undefined
terms.
Building on this foundation, we can then define additional terms. Once
the terminology is sufficiently developed, certain properties (characteristics)
of the system become apparent.
These properties are known as axioms or postulates of the system;
more generally, such statements are called assumptions.

6. A Mathematical
System
Once we have developed a vocabulary and accepted certain
postulates, many principles follow logically as we apply deductive
methods. These statements can be proved and are called theorems.
The following box summarizes the components of a mathematical
system (sometimes called a logical system or deductive system).

7. Undefined Terms
Words that do not have formal
definitions but there is an
agreement about what they
mean.

8. A POINT is the most basic building
block of geometry.
• It has no size.
• It only has location
You present a point with a dot , and you
name it with a capital letter.
Point

9. A LINE is a straight continuous
arrangement of infinitely many
points. It has infinite length but no
thickness. It extends forever in
BOTH directions.
Line
m

10. A plane has length and width but no
THICKNESS. It extends along its
length and width.
Plane

11. COLLINEAR – three or more points
on the same side
Collinear Points

12. COPLANAR – three or more points
on the same side.
Coplanar Points

13. Defined Terms
Terms that can be described
using known terms like point or
line.

14. LINE SEGMENT consist of two endpoints
A and all on AB that are between points
A and B.
Segment

15. A line which starts at one point and
goes the other direction infinitely.
Ray

16. INTERSECT two or more geometric
figures intersect if they have one or
more points bin common
Intersection

17. EXAMPLE 1: Name points, lines, and planes
a.Give two other names for PQ and for plane
R.
b.Name three points that are collinear.
c.Name four points that are coplanar.
a. Other names for PQ are QP and line n.
Other names for plane R are plane SVT and plane PTV.
b. Points S, P, and T lie on the same line, so they are
collinear. Points S, P, T,and V lie in the same plane, so they
are coplanar.
SOLUTION

18. EXAMPLE 2: Name segments, rays, and opposite rays
a. Give another name for line GH.
b. Name all rays with endpoint J .
Which of these rays are opposite
rays?
SOLUTION
a. Another name for GH is HG .
b. The rays with endpoint J are JE ,
JG , JF , and JH . The
pairs of opposite rays with
endpoint J are JE and JF , and JG
and JH .

19.  A line is made up of an infinite
number of points and is
considered to be straight. To
name a line, pick any two points
on the line (in any order) and
place a ↔ above them.
 A plane is a flat surface that
extends infinitely along its width
and length. You represent it with
a 4-sided figure. To name a
plane, a script capital letter is
used.
Examples
A
C
B
AB or BA
AC or CA
BC or CB

 

 

 

 

 

 

 

 

 

 

 

 

 

 
  


 

 

 

 

 

 

 

 

 

 

 

 

 

 
  


 

 

 

 

 

 

 

 

 

 

 

 

 

 
  

P
Lets try this!

20.  Collinear points are
points on the same
line.
 ANY 2 points will
ALWAYS be collinear
 Coplanar points are
points on the same
plane.
 ANY 3 points will
ALWAYS be coplanar
Examples
A
C
B
D
Are the following points collinear?
1) A and B ______
2) A and B and D ___
3) A and B and C ____
YES
NO
YES
P
E
F
G
H
I
Are the following points
coplanar?
1) E and F and G ______
2) E ,F ,G, H ______
3) F, G, H, I ____
YES
YES
NO

21.  A ray is a part of a line that
starts at a point called its
endpoint, and then extends
infinitely in one direction.
To name a ray, you need
two points. The first point is
its endpoint. This indicates
where the ray starts. The
other point is any other
point on the ray. You then
put a → symbol above
those two points.
A
C
B
Ray AB starts at A
extends towards point
B - another way to say
AB is ____
If you say CA that is a
different ray
AC

22.  A line segment is a part of
a line with a beginning and
an end. The point at the
beginning and the point at
the end are called the
endpoints. To name a
segment you use its
endpoints (in either order)
then place a − symbol
above them.
A
C
B
AB or BA
CB or BC
AC or CA

23.  Two segments are if
they have the same length. The
symbol for is congruent to is_____.
Never use a congruent symbol with
a number!!!
 There are 2 ways to write “the length
of a segment”
Equal sign
Or mAB = “m” stands for measure of”

congruent

24.  To bisect an object
means to cut it in half.
You can bisect an angle or
a line segment
To show a bisector you
mark the congruent parts
A
B
C
D
BD is the angle
bisector of < ABC

25.  A midpoint of a segment is a
point that is halfway between
the endpoints. A midpoint
bisects the segment.
B is the midpoint of AC
Formula for midpoint
A C
B
1 2 1 2
,
2 2
x x y y
 
 
 
 

26. Pick-up protractor on front table
A Protractor is a geometric tool used to measure
an angle and to draw an angle.
 Angles are measured in degrees.
An angle is formed by two rays
that share a common endpoint.
The vertex of the angle is the
common endpoint of the two rays.
Angles that have the same
measure are called congruent
angles.
37º

27.  An angle bisector is a ray that
divides an angle into two congruent
angles.
49º
49º

28. 3 methods to name an angle
1. Use three points that make up that angle, the vertex
must be in the middle
2. Use the number or letter in the interior of the angle
3. Use a single letter (be careful about other angles)
A
B
C
< ABC or < CBA
2 < 2
A F

29. Speed test:
Write down in complete
sentences and in your own
words 3 things that you
learned today.

30. Euclid’s Axioms
 Things which are equal to the same thing are equal to
one another.
 i.e. If A = C & B = C, then A = B.
 Here A, B & C are same kind of things.
 If equals are added to equals, the whole are equal
 i.e. If A = B & C = D, then A + C = B + D
 Also, A = B then this implies that A + C = B + C.
 If equals are subtracted from equals, the remainders
are equal.
 Things which coincide with one another are equal to

31. 31
Initial Postulates
Recall that a postulate is a statement that is assumed
to be true.
Postulate 1
Through two distinct points, there is exactly one line.
Postulate 1 is sometimes stated
in the form “Two points determine
a line.” See Figure 1, in which
points C and D determine exactly
one line, namely,
Figure 1

32. 32
Initial Postulates
Of course, Postulate 1 also implies that there is a unique line
segment determined by two distinct points used as endpoints.
In Figure 2, points A and B determine
Figure 2

33. 33
Example 2
In Figure 3, how many distinct lines can be drawn
through
a) point A?
b) both points A and B at the
same time?
c) all points A, B, and C at the
same time?
Solution:
a) An infinite (countless) number
b) Exactly one
c) No line contains all three points.
Figure 3

34. 34
Initial Postulates
The symbol for line segment AB, named by its endpoints,
is
Omission of the bar from , as in AB, means that we are
considering the length of the segment. These symbols are
summarized in Table 1.3.

35. 35
Initial Postulates
A ruler is used to measure the length of a line segment
such as
This length may be represented by AB or BA (the order
of A and B is not important). However, AB must be a
positive number.

36. 36
Initial Postulates
Postulate 2 (Ruler Postulate)
The measure of any line segment is a unique positive
number.
We wish to call attention to the term unique and to the
general notion of uniqueness.
The Ruler Postulate implies the following:
1. There exists a number measure for each line segment.
2. Only one measure is permissible.

37. 37
Initial Postulates
Characteristics 1 and 2 are both necessary for uniqueness!
Other phrases that may replace the term unique include
One and only one
Exactly one
One and no more than one
A more accurate claim than the commonly heard statement
“The shortest distance between two points is a straight line”
is found in the following definition.

38. 38
Initial Postulates
Definition
The distance between two points A and B is the length of
the line segment that joins the two points.
Postulate 3 (Segment-Addition Postulate)
If X is a point of and A-X-B, then AX + XB = AB.

39. 39
Initial Postulates
Definition
Congruent () line segments are two line segments that
have the same length.
In general, geometric figures that can be made to coincide
(fit perfectly one on top of the other) are said to be
congruent.
The symbol  is a combination of the symbol ~, which
means that the figures have the same shape, and =, which
means that the corresponding parts of the figures have the
same measure.

40. 40
Initial Postulates
In Figure 4, but (meaning that and
are not congruent). Does it appear that
Figure 4

41. 41
Initial Postulates
Definition
The midpoint of a line segment is the point that separates
the line segment into two congruent parts.
In Figure 5, if A, M, and B are
collinear and , then M is
the midpoint of . Equivalently,
M is the midpoint of if AM = MB.
Also, if , then is
described as a bisector of . Figure 5

42. 42
Initial Postulates
If M is the midpoint of in Figure 5, we can draw any of
these conclusions:
AM = MB MB = (AB) AB = 2(MB)
AM = (AB) AB = 2(AM)

43. 43
Initial Postulates
Definition
Ray AB, denoted by is the union of and all points X
on such that B is between A and X.
In Figure 6, and are shown in that order;
note that and are not the same ray.
Figure 6

44. 44
Initial Postulates
Opposite rays are two rays with a common endpoint; also,
the union of opposite rays is a straight line.
In Figure 7, and are opposite rays.
Figure 7

45. 45
Initial Postulates
The intersection of two geometric figures is the set of
points that the two figures have in common.
In everyday life, the intersection of Bradley Avenue and Neil
Street is the part of the roadway that the two roads have in
common (Figure 8).
Figure 8

46. 46
Initial Postulates
Postulate 4
If two lines intersect, they intersect at a point.
When two lines share two (or more) points, the lines
coincide; in this situation, we say there is only one line.
In Figure 7, and are the same as In Figure
9, lines ℓ and m intersect at point P.
Figure 9
Figure 7

47. 47
Initial Postulates
Definition
Parallel lines are lines that lie in the same plane but do not
intersect.
Another undefined term in geometry is plane. A plane is two-
dimensional; that is, it has infinite length and infinite width but no
thickness.
Except for its limited size, a flat surface such as the top of a
table could be used as an example of a plane.

48. 48
Initial Postulates
An uppercase letter can be used to name a plane. Because
a plane (like a line) is infinite, we can show only a portion of
the plane or planes, as in Figure 10.
Figure 10

49. 49
Initial Postulates
A plane is two-dimensional, consists of an infinite number of
points, and contains an infinite number of lines.
Two distinct points may determine (or “fix”) a line; likewise,
exactly three noncollinear points determine a plane.
Just as collinear points lie on the same line, coplanar
points lie in the same plane.

50. 50
Initial Postulates
In Figure 11, points B, C, D, and E are coplanar, whereas A,
B, C, and D are noncoplanar.
Figure 11

51. 51
Initial Postulates
Points shown in figures are generally assumed to be
coplanar unless otherwise stated. For instance, points A, B,
C, D, and E are coplanar in Figure 12, as are points F, G,
H, J, and K in Figure 13.
Figure 12 Figure 13

52. 52
Initial Postulates
Postulate 5
Through three noncollinear points, there is exactly one
plane.
On the basis of Postulate 5, we can see why a
three-legged table sits evenly but a four-legged table would
“wobble” if the legs were of unequal length.
Space is the set of all possible points. It is
three-dimensional, having qualities of length, width, and
depth. When two planes intersect in space, their
intersection is a line.

53. 53
Initial Postulates
An opened greeting card suggests this relationship, as does
Figure 14. This notion gives rise to our next postulate.
Postulate 6
If two distinct planes intersect,
then their intersection is a line.
The intersection of two planes
is infinite because it is a line.
See Figure 14.
Figure 14

54. 54
Initial Postulates
If two planes do not intersect, then they are parallel.
The parallel vertical planes R and S in Figure 15 may
remind you of the opposite walls of your classroom.
The parallel horizontal planes M and N in Figure 16
suggest the relationship between ceiling and floor.
Figure 16
Figure 15

55. 55
Initial Postulates
Imagine a plane and two points of that plane, say points A
and B. Now think of the line containing the two points and
the relationship of to the plane. Perhaps your
conclusion can be summed up as follows.
Postulate 7
Given two distinct points in a plane, the line containing
these points also lies in the plane.

56. Any Questions?