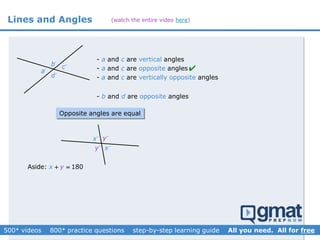
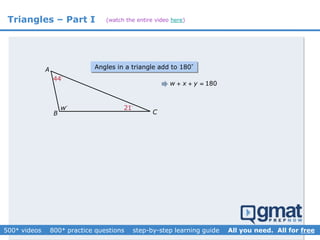
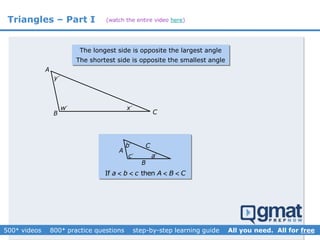
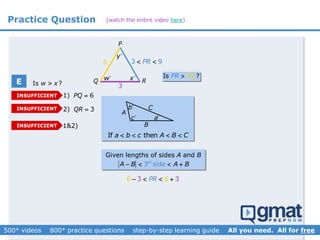
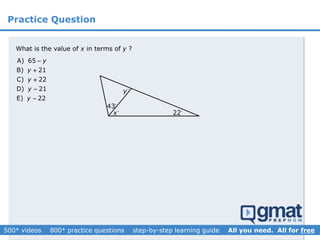
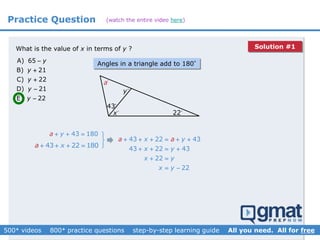
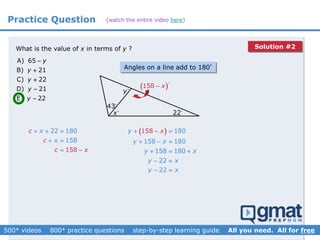
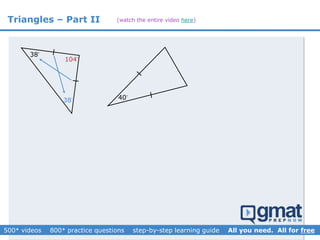
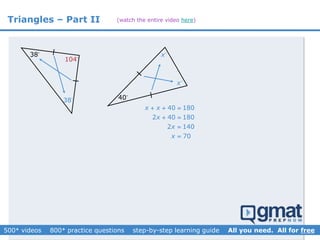
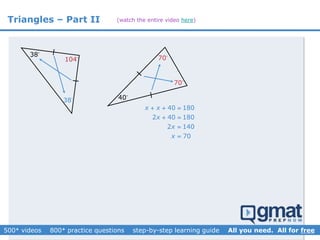
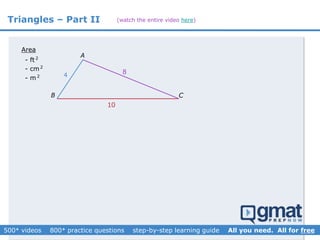
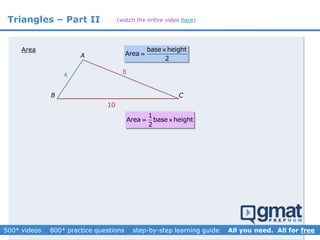
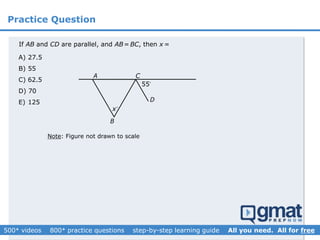
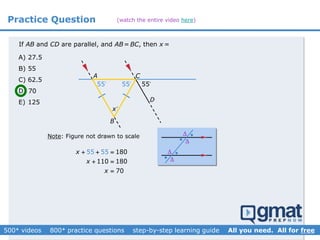
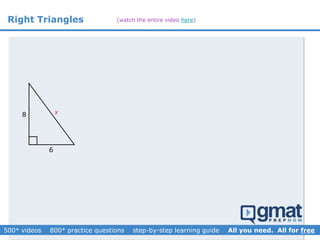
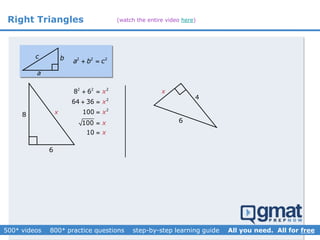
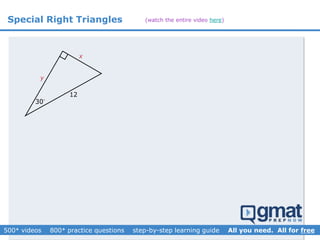
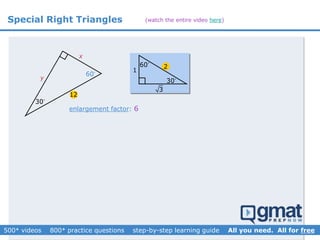
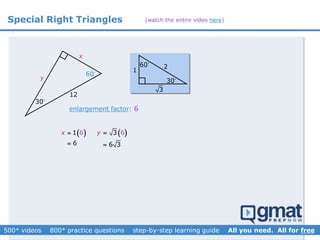
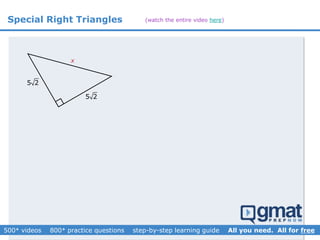
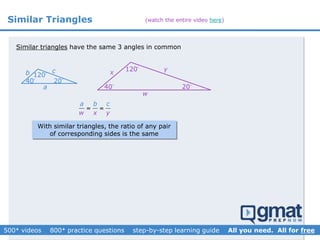
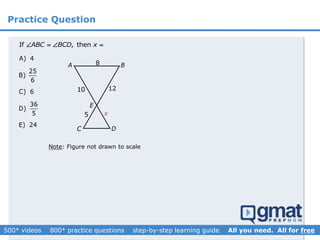
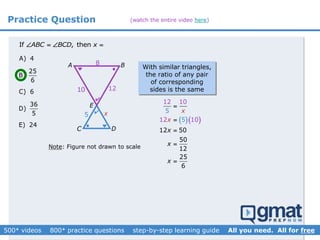
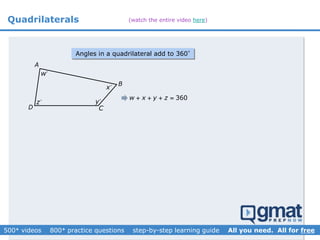
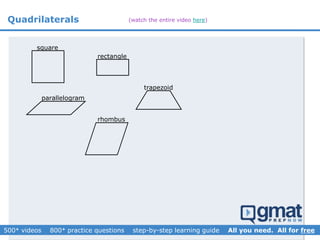
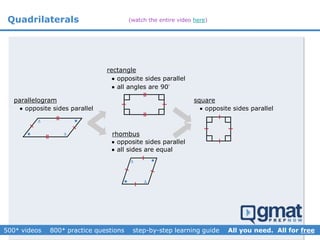
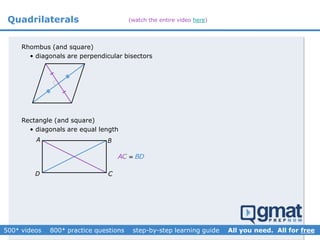
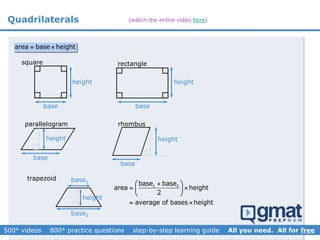
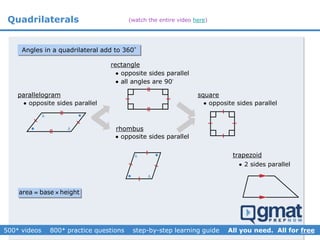
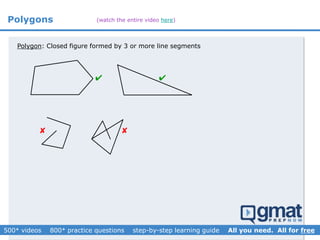
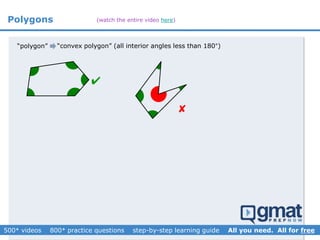
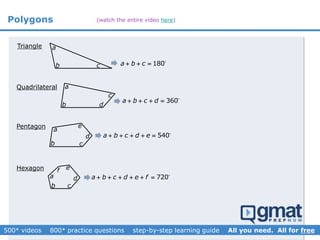
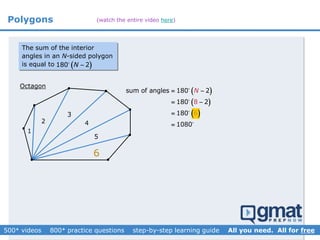
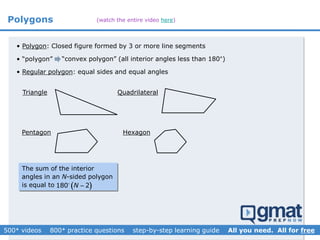
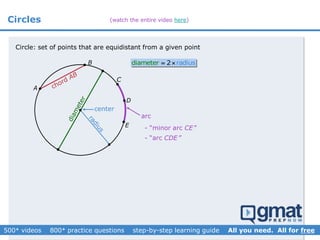
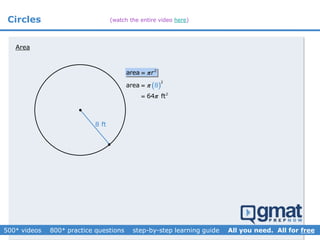
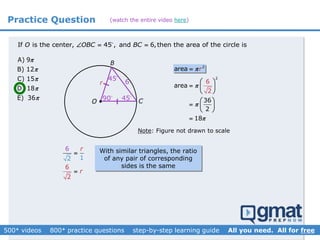
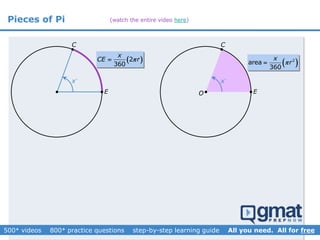
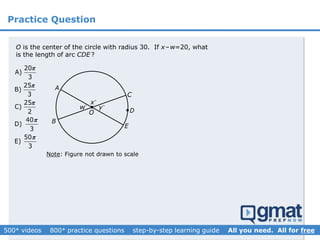
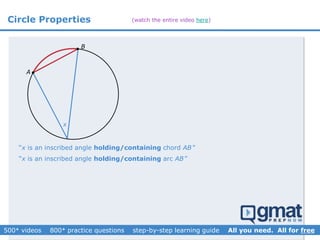
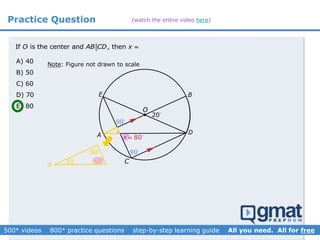
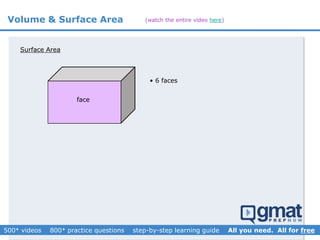
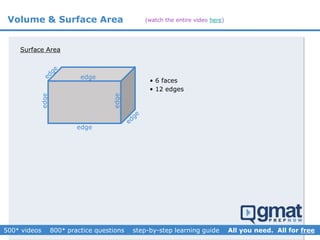
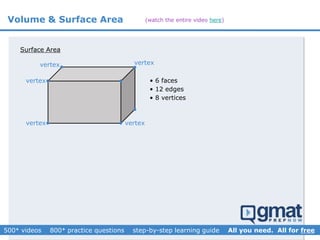
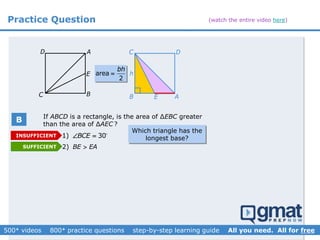
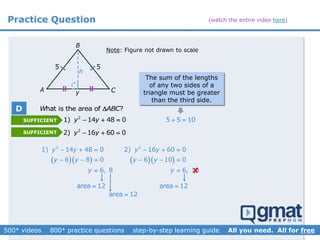
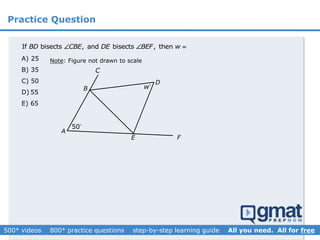
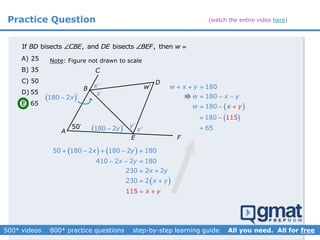
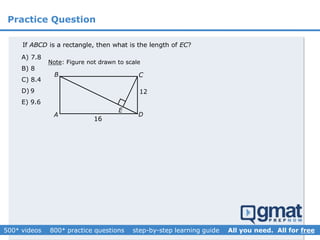
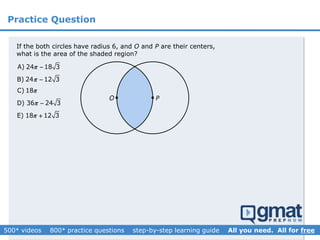
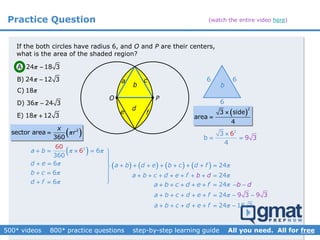
This document provides an overview and screenshots from a GMAT geometry module that covers key geometry concepts and includes practice questions. The module consists of 42 videos covering lines, angles, triangles, area of triangles, and strategies for solving geometry problems. It emphasizes important concepts like classifying triangles, properties of angles and sides, calculating area, and techniques for visualizing and solving problems. The screenshots are intended to highlight specific topics from each video at a high level, and links are provided to watch the full videos for more detailed explanations.