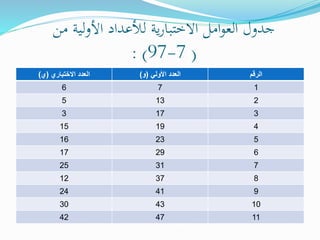
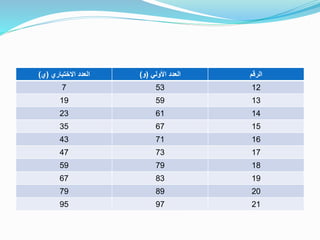
تناقش الوثيقة طرق اختبار قابلية القسمة على الأعداد الأولية، مع التركيز على العدد 11. تتضمن البحث وحدات تعليمية حول المفاهيم الرياضية المتعلقة بالأعداد الأولية، وتقديم أمثلة عملية لاختبار قابلية القسمة. كما تشير الوثيقة إلى طرق مختلفة لإيجاد ناتج القسمة على الأعداد.

1. ‫إعداد‬:‫المولى‬ ‫فضل‬ ‫عوض‬ ‫ياسر‬ ‫االستاذ‬
‫التربية‬ ‫بكالريوس‬
‫الخرطوم‬ ‫جامعة‬ ‫التربية‬ ‫كلية‬2006
‫ت‬:0964641141

2. ‫المقدمة‬:
‫في‬ ‫سنوات‬ ‫عشر‬ ‫من‬ ‫ألكثر‬ ‫استمرت‬ ‫دراسة‬ ‫بعد‬‫لمعرفة‬ ‫محاولة‬‫المزي‬‫عن‬ ‫د‬
‫األعداد‬ ‫و‬ ‫الطبيعية‬ ‫األعداد‬ ‫عالقة‬‫األولية‬‫لبع‬ ‫خاللها‬ ‫من‬ ‫التوصل‬ ‫تم‬‫ض‬
‫القواعد‬‫الطب‬ ‫األعداد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبار‬ ‫كيفية‬ ‫عن‬ ‫التطبيقات‬ ‫و‬‫على‬ ‫يعية‬
‫األعداد‬‫األولية‬‫ايجاد‬ ‫و‬‫الرياضية‬ ‫المعادالت‬ ‫توضح‬ ‫كما‬ ‫القسمة‬ ‫ناتج‬

3. ‫البحث‬ ‫موضوع‬:
‫يشتمل‬‫وحدات‬ ‫ثالث‬ ‫على‬ ‫البحث‬:
‫األولى‬ ‫الوحدة‬:
‫األولي‬ ‫للعدد‬ ‫خاصة‬ ‫معادالت‬ ‫و‬ ‫قواعد‬11‫قسمة‬ ‫قابلية‬ ‫اختبار‬ ‫كيفية‬ ‫عن‬
‫القسمة‬ ‫ناتج‬ ‫ايجاد‬ ‫و‬ ‫الطبيعية‬ ‫األعداد‬
‫الوحدة‬‫الثانية‬:
‫األولية‬ ‫األعداد‬ ‫على‬ ‫الطبيعية‬ ‫األعداد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبار‬
‫الوحدة‬‫الثالثة‬:
‫األولية‬ ‫األعداد‬ ‫على‬ ‫الطبيعية‬ ‫األعداد‬ ‫قسمة‬ ‫ناتج‬ ‫ايجاد‬

4. ‫البحث‬ ‫حيتويها‬ ‫الىت‬ ‫املعادالت‬ ‫و‬ ‫اعد‬‫و‬‫الق‬:
1-‫االختباري‬ ‫العامل‬:
‫االختباري‬ ‫العامل‬=‫من‬ ‫أكبر‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬100-99
2-‫ط‬ ‫باستخدام‬ ‫األولية‬ ‫األعداد‬ ‫على‬ ‫الطبيعية‬ ‫األعداد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبار‬ ‫معادلة‬‫ريقة‬
‫العامل‬‫األفقي‬ ‫االختباري‬:
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )‫صفر‬ ‫أو‬ ‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬ ‫عدد‬
3-‫ط‬ ‫باستخدام‬ ‫األولية‬ ‫األعداد‬ ‫على‬ ‫الطبيعية‬ ‫األعداد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبار‬ ‫معادلة‬‫ريقة‬
‫المضاعف‬‫الهرمي‬ ‫العشري‬:
‫ن‬/‫م‬–‫م‬/‫ن‬=َ‫ا‬‫صفر‬ ‫او‬ ‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬ ‫عدد‬
4-‫منازل‬ ‫ثالث‬ ‫من‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬ ‫ايجاد‬
‫عشرية‬=‫ي‬+99
5-‫ايجاد‬‫التى‬ ‫العشرية‬ ‫المنازل‬ ‫و‬ ‫عشرية‬ ‫منازل‬ ‫أربعة‬ ‫من‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬‫تليه‬
6-‫األولي‬ ‫العدد‬ ‫على‬ ‫عشرية‬ ‫منازل‬ ‫ثالثة‬ ‫من‬ ‫مضاعف‬ ‫أول‬ ‫قسمة‬ ‫ناتج‬ ‫ايجاد‬

6. ً‫ا‬‫ل‬‫أو‬:ً‫قابليةًالقسمةًعلى‬11:
‫الختبار‬‫على‬ ‫عدد‬ ‫أي‬ ‫قسمة‬ ‫قابلية‬11‫يتكون‬ ‫زوج‬ ‫كل‬ ‫أزواج‬ ‫إلى‬ ‫العدد‬ ‫م‬ّ‫س‬‫نق‬
‫عشريتين‬ ‫منزلتين‬ ‫من‬,‫مضاعفات‬ ‫من‬ ‫االزواج‬ ‫هذه‬ ‫جمع‬ ‫حاصل‬ ‫كان‬ ‫اذا‬
‫العدد‬11‫على‬ ‫القسمة‬ ‫يقبل‬ ‫العدد‬ ‫فإن‬11,‫من‬ ‫الجمع‬ ‫ناتج‬ ‫يكن‬ ‫لم‬ ‫إذا‬ ‫أما‬
‫مضاعفات‬11‫على‬ ‫القسمة‬ ‫يقبل‬ ‫ال‬ ‫العدد‬ ‫فإن‬11.
‫مالحظة‬:
‫العشرات‬ ‫و‬ ‫األحاد‬ ‫منزلة‬ ‫من‬ ‫األول‬ ‫الزوج‬ ‫يتكون‬,‫يت‬ ‫الثاني‬ ‫الزوج‬ ‫أما‬‫كون‬
‫هكذا‬ ‫و‬ ‫اآلالف‬ ‫و‬ ‫المئات‬ ‫من‬.

7. ‫مثال‬(1)
‫على‬ ‫القسمة‬ ‫قابلية‬ ‫اختبار‬11‫للعدد‬253:
‫األول‬ ‫الزوج‬=53‫الثاني‬ ‫الزوج‬=02
53+02=55
55‫العدد‬ ‫مضاعفات‬ ‫من‬11
‫العدد‬ ‫يقبل‬253‫على‬ ‫القسمة‬11.

8. ‫مثال‬(2)
‫على‬ ‫القسمة‬ ‫قابلية‬ ‫اختبار‬11‫للعدد‬1298:
‫األول‬ ‫الزوج‬=98‫الثاني‬ ‫الزوج‬=12
98+12=110
110‫العد‬ ‫مضاعفات‬ ‫من‬11(11×10)
‫العدد‬ ‫يقبل‬1298‫على‬ ‫القسمة‬11.

9. ‫مثال‬(3)
‫على‬ ‫القسمة‬ ‫قابلية‬ ‫اختبار‬11‫للعدد‬1318:
‫األول‬ ‫الزوج‬=18‫الثاني‬ ‫الزوج‬=13
18+13=31
31‫العدد‬ ‫مضاعفات‬ ‫من‬ ‫ليس‬11
‫العدد‬ ‫يقبل‬ ‫ال‬1318‫على‬ ‫القسمة‬11

10. ‫مثال‬(4)
‫على‬ ‫القسمة‬ ‫قابلية‬ ‫اختبار‬11‫للعدد‬15730:
‫األول‬ ‫الزوج‬=30‫الثاني‬ ‫الزوج‬=57‫الثالث‬ ‫الزوج‬=
01
30+57+1=88
88‫العد‬ ‫مضاعفات‬ ‫من‬11
‫العدد‬ ‫يقبل‬15730‫على‬ ‫القسمة‬11.

11. ‫مثال‬(5)
‫على‬ ‫القسمة‬ ‫قابلية‬ ‫اختبار‬11‫للعدد‬16060:
‫االول‬ ‫الزوج‬=60‫الثاني‬ ‫الزوج‬=60‫الثالث‬ ‫الزوج‬=01
60+60+1=121
121‫العد‬ ‫مضاعفات‬ ‫من‬11(11×11)
‫العدد‬ ‫يقبل‬16060‫على‬ ‫القسمة‬11.

12. ‫مثال‬(6)
‫على‬ ‫القسمة‬ ‫قابلية‬ ‫اختبار‬11‫للعدد‬178959:
‫األول‬ ‫الزوج‬=59‫الثاني‬ ‫الزوج‬=89‫الثالث‬ ‫الزوج‬=17
59+89+17=165
‫قسمة‬ ‫قابلية‬ ‫اختبار‬ ‫يمكن‬165‫على‬11‫الطريقة‬ ‫بنفس‬.
65+1=66
165‫على‬ ‫القسمة‬ ‫يقبل‬11
‫العدد‬ ‫يقبل‬178959‫على‬ ‫القسمة‬11.

13. ‫مثال‬(7)
‫على‬ ‫القسمة‬ ‫قابلية‬ ‫اختبار‬11‫للعدد‬247567:
‫األول‬ ‫الزوج‬=67‫الثاني‬ ‫الزوج‬=75‫الثالث‬ ‫الزوج‬=24
67+75+24=166
166‫العد‬ ‫مضاعفات‬ ‫من‬ ‫ليس‬11
‫العدد‬ ‫يقبل‬ ‫ال‬247567‫على‬ ‫القسمة‬11.

14. ‫مثال‬(8)
‫على‬ ‫القسمة‬ ‫قابلية‬ ‫اختبار‬11‫للعدد‬1932612:
‫األول‬ ‫الزوج‬=12‫الثاني‬ ‫الزوج‬=26
‫الثالث‬ ‫الزوج‬=93‫الرابع‬ ‫الزوج‬=01
12+26+93+1=132
132‫العد‬ ‫مضاعفات‬ ‫من‬11(11×12)
‫العدد‬ ‫يقبل‬1932612‫على‬ ‫القسمة‬11.

15. ً‫ا‬‫ا‬‫ثاني‬:ً‫اجيادًناتجًالقسمةًعلى‬11:
‫عشرية‬ ‫منازل‬ ‫ثالثة‬ ‫من‬ ‫المكونة‬ ‫األعداد‬:
‫عدد‬ ‫قسمة‬ ‫ناتج‬ ‫اليجاد‬"‫على‬ ‫القسمة‬ ‫يقبل‬11"‫منازل‬ ‫ثالث‬ ‫من‬ ‫مكون‬
‫ف‬ ‫العدد‬ ‫جعل‬ ‫و‬ ‫العشرات‬ ‫منزلة‬ ‫في‬ ‫الموجود‬ ‫العدد‬ ‫بحذف‬ ‫نقوم‬ ‫عشرية‬‫ي‬
‫مكانه‬ ‫المئات‬ ‫منزلة‬.
‫اذا‬‫يساوي‬ ‫أو‬ ‫من‬ ‫أكبر‬ ‫المئات‬ ‫و‬ ‫األحاد‬ ‫منزلة‬ ‫في‬ ‫الرقمين‬ ‫مجموع‬ ‫كان‬11
,‫منزلة‬ ‫في‬ ‫الموجود‬ ‫العدد‬ ‫من‬ ‫صحيح‬ ‫واحد‬ ‫بطرح‬ ‫الناتج‬ ‫الحالة‬ ‫هذه‬ ‫في‬
‫المئات‬.

16. ‫مثال‬(1: )
‫قسمة‬ ‫ناتج‬132÷11=12
‫الرقم‬ ‫بحذف‬ ‫نقوم‬3‫الموجود‬ ‫الواحد‬ ‫نضع‬ ‫و‬ ‫العشرات‬ ‫منزلة‬ ‫في‬ ‫الموجود‬
‫المحذوف‬ ‫الرقم‬ ‫مكان‬ ‫العشرات‬ ‫منزلة‬ ‫في‬ ‫المئات‬ ‫في‬.

17. ‫مثال‬(2:)
‫قسمة‬ ‫ناتج‬308÷11=28
ً‫ال‬‫أو‬ ‫العشرات‬ ‫منزلة‬ ‫في‬ ‫الموجود‬ ‫الصفر‬ ‫نحذف‬,‫الرقم‬ ‫نجعل‬ ‫و‬3
‫العشرات‬ ‫منزلة‬ ‫في‬ ‫المحذوف‬ ‫الصفر‬ ‫مكان‬ ‫المئات‬ ‫منزلة‬ ‫في‬ ‫الموجود‬,‫بما‬
‫أن‬8+3=11‫الرقم‬ ‫من‬ ‫صحيح‬ ‫واحد‬ ‫نطرح‬ ‫الحالة‬ ‫هذه‬ ‫في‬3‫يصبح‬ ‫حيث‬
2‫الناتج‬ ‫يكون‬ ‫و‬28.

18. ‫مثال‬(3:)
‫على‬ ‫القسمة‬ ‫ناتج‬ ‫ايجاد‬11‫للعدد‬429:
‫الرقم‬ ‫نحذف‬2‫العشرات‬ ‫خانة‬ ‫من‬
‫أن‬ ‫بما‬4+9=13,13>11
‫هو‬ ‫و‬ ‫المئات‬ ‫منزلة‬ ‫في‬ ‫الموجود‬ ‫العدد‬ ‫من‬ ‫صحيح‬ ‫واحد‬ ‫نطرح‬ ‫إذن‬4
‫ليصبح‬3
‫قسمة‬ ‫ناتج‬429÷11=39.

19. ‫مثال‬(4:)
‫على‬ ‫القسمة‬ ‫ناتج‬ ‫اوجد‬11‫للعدد‬671:
‫الرقم‬ ‫نحذف‬7‫العشرات‬ ‫خانة‬ ‫من‬
‫أن‬ ‫بما‬1+6=7,7<11
‫العدد‬ ‫نضع‬ ‫إذن‬6‫العشرات‬ ‫منزلة‬ ‫في‬ ‫هو‬ ‫كما‬
‫قسمة‬ ‫ناتج‬671÷11=61.


20. ‫عشرية‬ ‫منازل‬ ‫أربعة‬ ‫من‬ ‫المكونة‬ ‫األعداد‬:
‫عدد‬ ‫قسمة‬ ‫ناتج‬ ‫اليجاد‬"‫على‬ ‫القسمة‬ ‫يقبل‬11"‫عشرية‬ ‫منازل‬ ‫أربعة‬ ‫من‬ ‫مكون‬:
‫العشرات‬ ‫منزلة‬ ‫في‬ ‫الموجود‬ ‫العدد‬ ‫نحذف‬.
‫في‬ ‫الموجود‬ ‫الرقم‬ ‫بمقدار‬ ‫اآلالف‬ ‫و‬ ‫المئات‬ ‫منزلة‬ ‫من‬ ‫المكون‬ ‫العدد‬ ‫من‬ ‫نطرح‬
‫اآلالف‬ ‫منزلة‬.
‫يساوي‬ ‫أو‬ ‫من‬ ‫أكبر‬ ‫المجموع‬ ‫كان‬ ‫اذا‬ ‫و‬ ‫المئات‬ ‫و‬ ‫االحاد‬ ‫منزلة‬ ‫فى‬ ‫االرقام‬ ‫نجمع‬
11‫المئات‬ ‫من‬ ‫المكون‬ ‫العدد‬ ‫من‬ ‫المطروح‬ ‫للعدد‬ ‫باإلضافة‬ ‫صحيح‬ ‫واحد‬ ‫نطرح‬‫و‬
‫اآلالف‬.
‫يساوي‬ ‫أو‬ ‫أكبرمن‬ ‫المجموع‬ ‫كان‬ ‫اذا‬ ‫اآلالف‬ ‫و‬ ‫العشرات‬ ‫منزلة‬ ‫فى‬ ‫االرقام‬ ‫نجمع‬
11‫اآلالف‬ ‫و‬ ‫المئات‬ ‫من‬ ‫المكون‬ ‫العدد‬ ‫من‬ ‫المطروح‬ ‫للعدد‬ ‫صحيح‬ ‫واحد‬ ‫نضيف‬.

21. ‫مثال‬(1:)
‫على‬ ‫القسمة‬ ‫ناتج‬ ‫اوجد‬11‫للعدد‬7381:
‫الرقم‬ ‫نحذف‬8‫العشرات‬ ‫خانة‬ ‫في‬ ‫الموجود‬.
1+3=4,4<11‫صحيح‬ ‫واحد‬ ‫نطرح‬ ‫ال‬
8+7=15,15>11‫صحيح‬ ‫واحد‬ ‫نضيف‬
73–7+1=67
‫قسمة‬ ‫ناتج‬7381÷11=671

22. ‫مثال‬(2:)
‫على‬ ‫القسمة‬ ‫ناتج‬ ‫اوجد‬11‫للعدد‬1243:
‫الرقم‬ ‫نحذف‬4‫العشرات‬ ‫خانة‬ ‫في‬ ‫الموجود‬.
3+2=5,5<11‫صحيح‬ ‫واحد‬ ‫نطرح‬ ‫ال‬
4+1=5,5<11‫صحيح‬ ‫واحد‬ ‫نضيف‬ ‫ال‬
12–1=11
‫قسمة‬ ‫ناتج‬1243÷11=113.

23. ‫مثال‬(3:)
‫على‬ ‫القسمة‬ ‫ناتج‬ ‫اوجد‬11‫للعدد‬7546:
‫الرقم‬ ‫نحذف‬4‫العشرات‬ ‫خانة‬ ‫في‬ ‫الموجود‬.
6+5=11‫صحيح‬ ‫واحد‬ ‫نطرح‬
4+7=11‫صحيح‬ ‫واحد‬ ‫نضيف‬
75–7–1+1=68
‫قسمة‬ ‫ناتج‬7546÷11=686

25. ‫اختبارًقابليةًقسمةًاألعدادًالطبيعيةًعلى‬ً‫األعداد‬
ً‫األولية‬
‫ا‬‫ال‬‫أو‬:‫األفقي‬ ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬
ً‫ا‬‫ثاني‬:‫الهرمي‬ ‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬

26. ‫اختبارًقابليةًقسمةًاألعدادًالطبيعيةًعلى‬ً‫األعداد‬
ً‫األوليةًباستخدامًالعاملًالختباري‬
‫االختباري‬ ‫العامل‬:
‫ع‬ ‫هنالك‬ ‫األولية‬ ‫األعداد‬ ‫على‬ ‫الطبيعية‬ ‫األعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬‫معين‬ ‫دد‬
‫االختب‬ ‫العامل‬ ً‫ا‬‫اصطالح‬ ‫عليه‬ ‫يطلق‬ ‫األولية‬ ‫األعداد‬ ‫يرادف‬ ‫أو‬ ‫يرافق‬‫اري‬.
‫االختباري‬ ‫العامل‬ ‫ايجاد‬ ‫كيفية‬:
‫االختباري‬ ‫العامل‬=‫أكبرمن‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬100–99.

‫أمثلة‬:
‫األولي‬ ‫للعدد‬ ‫االختباري‬ ‫العامل‬7=105–99=6
‫األولي‬ ‫للعدد‬ ‫االختباري‬ ‫العامل‬19=114–99=15
‫األولي‬ ‫للعدد‬ ‫االختباري‬ ‫العامل‬23=115–99=16

27. ‫من‬ ‫لية‬‫و‬‫األ‬ ‫لألعداد‬ ‫ية‬‫ر‬‫االختبا‬ ‫امل‬‫و‬‫الع‬ ‫جدول‬
(7-97: )
‫الرقم‬‫العدد‬‫األولي‬(‫و‬)‫العدد‬‫االختباري‬(‫ي‬)
176
2135
3173
41915
52316
62917
73125
83712
94124
104330
114742

28. ‫الرقم‬‫العدد‬‫األولي‬(‫و‬)‫العدد‬‫االختباري‬(‫ي‬)
12537
135919
146123
156735
167143
177347
187959
198367
208979
219795

29. ‫األولية‬ ‫األعداد‬ ‫على‬ ‫الطبيعية‬ ‫األعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬:
ً‫ال‬‫أو‬:‫األفقي‬ ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫مصطلحات‬ ‫و‬ ‫رموز‬:
‫ط‬ ‫بالرمز‬ ‫الطبيعي‬ ‫للعدد‬ ‫نرمز‬
‫و‬ ‫بالرمز‬ ‫األولي‬ ‫للعدد‬ ‫نرمز‬
‫ي‬ ‫بالرمز‬ ‫االختباري‬ ‫للعامل‬ ‫نرمز‬
‫هو‬ ‫الطبيعي‬ ‫العدد‬ ‫ان‬ ‫افرض‬321
‫س‬ ‫فإن‬=21‫ص‬=3
‫أو‬4321
‫س‬ ‫فإن‬=21‫ص‬=43

30. ‫أو‬54321
‫س‬ ‫فإن‬=21‫ص‬=543
‫أو‬654321
‫س‬ ‫فإن‬=21‫ص‬=6543
‫العدد‬ ‫هي‬ ‫ص‬ ‫و‬ ‫العشرات‬ ‫و‬ ‫اآلحاد‬ ‫منزلة‬ ‫من‬ ‫المكون‬ ‫العدد‬ ‫هي‬ ‫س‬ ‫ان‬ ‫أي‬
‫الطبيعي‬ ‫للعدد‬ ‫الباقية‬ ‫العشرية‬ ‫المنازل‬ ‫من‬ ‫المكون‬
‫افقية‬ ‫بصورة‬ ‫ص‬ ‫في‬ ‫تزداد‬ ‫العشرية‬ ‫المنازل‬ ‫عدد‬ ‫ألن‬ ‫أفقي‬ ‫سمي‬
‫ص‬=3‫ص‬ ‫أو‬=43‫ص‬ ‫أو‬=543

31. ‫الخطوات‬:
‫س‬ ‫اجمع‬+‫ص‬
‫ص‬ ‫ي‬ ‫اضرب‬
‫بينهما‬ ‫الفرق‬ ‫خذ‬
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )‫صفر‬ ‫أو‬ ‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬ ‫عدد‬

32. ً‫ا‬‫ثاني‬:‫الهرمي‬ ‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫مصطلحات‬ ‫و‬ ‫رموز‬:
‫عشرية‬ ‫منزلة‬ ‫أي‬ ‫بين‬ ‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫ألن‬ ‫هرمي‬ ‫عليه‬ ‫يطلق‬‫األخر‬ ‫و‬‫ى‬
‫الهرمي‬ ‫المدرج‬ ‫شكل‬ ‫تأخذ‬.
‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ً‫ال‬‫مث‬7‫هي‬:
105
1001
10003
100002
1000006
‫ط‬ ‫بالرمز‬ ‫الطبيعي‬ ‫للعدد‬ ‫نرمز‬
‫ال‬ ‫لمنازل‬ ‫مساوية‬ ‫عشرية‬ ‫منازل‬ ‫من‬ ‫يتكون‬ ‫االولي‬ ‫للعدد‬ ‫مضاعف‬ ‫ألول‬ ‫نرمز‬‫عدد‬
‫ش‬ ‫بالرمز‬ ‫اختباره‬ ‫المراد‬ ‫الطبيعي‬

33. ‫هو‬ ‫الطبيعي‬ ‫العدد‬ ‫ان‬ ‫افرض‬321
‫م‬ ‫فإن‬=21‫ن‬=3
‫أو‬4321
‫م‬ ‫فإن‬=21‫ن‬=43
‫أو‬54321
‫م‬ ‫فإن‬=321‫ن‬=54
‫أو‬654321
‫م‬ ‫فإن‬=321‫ن‬=654
‫ان‬ ‫نالحظ‬:
‫م‬=‫زوجي‬ ‫العشرية‬ ‫المنازل‬ ‫عدد‬ ‫كان‬ ‫إذا‬ ‫المنازل‬ ‫عدد‬ ‫في‬ ‫ن‬
‫م‬=‫ن‬+1‫فردي‬ ‫العشرية‬ ‫المنازل‬ ‫عدد‬ ‫كان‬ ‫أذا‬ ‫العشرية‬ ‫المنازل‬ ‫عدد‬ ‫في‬

34. ‫االختبار‬ ‫خطوات‬:
‫الطبيعي‬ ‫العدد‬ ‫منها‬ ‫يتكون‬ ‫التى‬ ‫العشرية‬ ‫المنازل‬ ‫عدد‬ ‫نحدد‬
‫لمناز‬ ‫مساوية‬ ‫عشرية‬ ‫منازل‬ ‫من‬ ‫يتكون‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬ ‫نوجد‬‫ل‬
‫الطبيعي‬ ‫العدد‬(‫ش‬)
‫م‬ ‫بالرموز‬ ‫األولي‬ ‫للعدد‬ ‫العشرية‬ ‫للمنازل‬ ‫نرمز‬/‫ن‬ ‫و‬/‫م‬ ‫حيث‬/=‫ح‬ ‫من‬ ‫م‬‫يث‬
‫ن‬ ‫و‬ ‫العشرية‬ ‫المنازل‬ ‫عدد‬/=‫العشرية‬ ‫المنازل‬ ‫حيث‬ ‫من‬ ‫ن‬
‫هو‬ ‫العدد‬ ‫ان‬ ‫افرض‬321‫هو‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫اول‬ ‫و‬105
‫م‬ ‫حيث‬=21‫ن‬=3
‫م‬/=5‫ن‬/=1

35. ‫العكسي‬ ‫بالضرب‬
‫ن‬/‫م‬–‫م‬/‫ن‬=‫صفر‬ ‫او‬ ‫األولي‬ ‫العدد‬ ‫مضاعف‬
‫هو‬ ‫العدد‬ ‫ان‬ ‫افرض‬4321‫هو‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫اول‬ ‫و‬1017
‫م‬ ‫حيث‬=21‫ن‬=43
‫م‬/=17‫ن‬/=10
‫العكسي‬ ‫بالضرب‬
‫ن‬/‫م‬–‫م‬/‫ن‬=10×21–17×43=‫األولي‬ ‫العدد‬ ‫مضاعف‬
‫ثالث‬ ‫من‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬ ‫اليجاد‬ ‫االختباري‬ ‫العامل‬ ‫نستخدم‬‫ة‬
‫عشرية‬ ‫منازل‬:
‫حيث‬:‫ي‬+99=‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬

36. ‫مثال‬:
‫األولي‬ ‫العدد‬(‫و‬)7
‫االختباري‬ ‫العامل‬(‫ي‬)‫هو‬6
6+99=105
105‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬7‫عشرية‬ ‫منازل‬ ‫ثالثة‬ ‫من‬
‫األولي‬ ‫العدد‬(‫و‬)19
‫االختباري‬ ‫العامل‬(‫ي‬)15
15+99=114
114‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬19‫عشرية‬ ‫منازل‬ ‫ثالثة‬ ‫من‬

37. ‫عشرية‬ ‫منازل‬ ‫أربعة‬ ‫من‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬ ‫اليجاد‬:
‫منازلة‬ ‫ثالثة‬ ‫من‬ ‫مضاعف‬ ‫ألول‬ ‫العشرات‬ ‫و‬ ‫األحاد‬ ‫منزلة‬ ‫من‬ ‫المكون‬ ‫العدد‬ ‫خذ‬
‫عشرية‬.
‫العدد‬ ‫اضرب‬×10.
‫االولي‬ ‫العدد‬ ‫على‬ ‫الضرب‬ ‫ناتج‬ ‫اقسم‬
‫أرب‬ ‫من‬ ‫األولي‬ ‫العدد‬ ‫مضاعف‬ ‫به‬ ‫يبدأ‬ ‫الذى‬ ‫الرقم‬ ‫يمثل‬ ‫القسمة‬ ‫ناتج‬ ‫باقي‬‫منازل‬ ‫عة‬
‫عشرية‬
‫هكذا‬ ‫و‬
‫من‬ ‫المكون‬ ‫الرقم‬ ‫نأخذ‬ ‫المعينة‬ ‫المنزلة‬ ‫في‬ ‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬ ‫اليجاد‬
‫باق‬ ‫يكون‬ ‫و‬ ‫األولي‬ ‫العدد‬ ‫على‬ ‫نقسم‬ ‫ثم‬ ‫السابقة‬ ‫للمنزلة‬ ‫العشرات‬ ‫و‬ ‫األحاد‬‫القسمة‬ ‫ي‬
‫المطلوبة‬ ‫للمنزلة‬ ‫مضاعف‬ ‫أول‬ ‫هو‬.

38. ‫مثال‬:
‫األولي‬ ‫للعدد‬ ‫العشرية‬ ‫المضاعفات‬ ‫اوجد‬7(‫المضاعف‬ ‫عليها‬ ‫نطلق‬
‫الهرمي‬ ‫العشري‬)
‫هو‬ ‫عشرية‬ ‫منازل‬ ‫ثالثة‬ ‫من‬ ‫مضاعف‬ ‫أول‬
6+99=105
‫عشرية‬ ‫منازل‬ ‫أربعة‬ ‫من‬ ‫المضاعف‬
5×10=50
50÷7=7‫الباقي‬ ‫و‬1
‫هو‬ ‫منازل‬ ‫أربعة‬ ‫من‬ ‫مضاعف‬ ‫أول‬1001

39. ‫منازل‬ ‫خمسة‬ ‫من‬ ‫المضاعف‬
1×10=10
10÷7=1‫الباقي‬ ‫و‬3
‫هو‬ ‫منازل‬ ‫خمسة‬ ‫من‬ ‫مضاعف‬ ‫أول‬10003
‫منازل‬ ‫ستة‬ ‫من‬ ‫المضاعف‬
3×10=30
30÷7=4‫الباقي‬ ‫و‬2
100002‫السادسة‬ ‫العشرية‬ ‫المنزلة‬ ‫من‬ ‫مضاعف‬ ‫أول‬ ‫هو‬
‫هكذا‬ ‫و‬

40. ‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬875‫االولي‬ ‫العدد‬ ‫على‬7:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=875‫و‬=7‫ي‬=6
‫س‬=75‫ص‬=8
‫س‬+‫ص‬=75+8=83
‫ص‬ ‫ي‬=6×7=48
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
48–83=‾35
‫العدد‬ ‫ان‬ ‫بما‬‾35=7×‾5
‫الطبيعي‬ ‫العدد‬ ‫اذن‬875‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬7

41. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=875‫ش‬=105
‫م‬=75‫ن‬=8
‫م‬/=5‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×75–5×8=
75–40=35
‫العدد‬ ‫ان‬ ‫بما‬35=7×5
‫الطبيعي‬ ‫العدد‬ ‫اذن‬875‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬7

42. ‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫القسمة‬ ‫قابلية‬ ‫اختبر‬3682‫االولي‬ ‫العدد‬ ‫على‬7
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=3682‫و‬=7‫ي‬=6
‫س‬=82‫ص‬=36
‫س‬+‫ص‬=82+36=118
‫ص‬ ‫ي‬=6×36=216
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
216–118=98
‫العدد‬ ‫ان‬ ‫بما‬98=7×14
‫الطبيعي‬ ‫العدد‬ ‫اذن‬3682‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬7

43. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=3682‫ش‬=1001
‫م‬=82‫ن‬=36
‫م‬/=1‫ن‬/=10
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
10×82–1×36=
820–36=784

44. ‫التطبيق‬ ‫بتكرار‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬:-

‫ط‬=784‫ش‬=105
‫م‬=84‫ن‬=7
‫م‬/=5‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×84–5×7=
84–35=49
‫العدد‬ ‫ان‬ ‫بما‬49=7×7
‫العدد‬ ‫اذن‬3682‫العدد‬ ‫مضاعفات‬ ‫من‬7

45. ‫مثال‬:
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبر‬81529‫االولي‬ ‫العدد‬ ‫علي‬7
‫اوال‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫الحل‬:-
‫ط‬=81529‫و‬=7‫ي‬=6
‫س‬=29‫ص‬=815
‫س‬+‫ص‬=29+815=844
‫ص‬ ‫ي‬=6×815=4890
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
4890-844=4046

46. ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫التطبيق‬ ‫وبتكرار‬:-
‫ط‬=4046‫و‬=7‫ي‬=6
‫س‬=46‫ص‬=40
‫س‬+‫ص‬=46+40=86
‫ص‬ ‫ي‬=6×40=240
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
240-86=154

47. ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫التطبيق‬ ‫وبتكرار‬:-
‫ط‬=154‫و‬=7‫ي‬=6
‫س‬=54‫ص‬=1
‫س‬+‫ص‬=54+1=55
‫ص‬ ‫ي‬=6×1=6
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
6-55=‾49
‫العدد‬ ‫ان‬ ‫بما‬‾49=7×‾7
‫الطبيعي‬ ‫العدد‬ ‫اذن‬81529‫العدد‬ ‫مضاعفات‬7

48. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=81529‫ش‬=10003
‫م‬=529‫ن‬=81
‫م‬/=3‫ن‬/=10
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
10×529–3×81=
5290–243=5047

49. ‫التطبيق‬ ‫بتكرار‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬:-
‫ط‬=5047‫ش‬=1001
‫م‬=47‫ن‬=50
‫م‬/=1‫ن‬/=10
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
10×47–1×50=
470–50=420

50. ‫التطبيق‬ ‫بتكرار‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬:-
‫ط‬=420‫ش‬=105
‫م‬=20‫ن‬=4
‫م‬/=5‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×20–5×4=
20–20=0
‫العدد‬ ‫اذن‬81529‫العدد‬ ‫مضاعفات‬ ‫من‬7

51. ‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبر‬489216‫االولي‬ ‫العدد‬ ‫علي‬7
‫اوال‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫الحل‬:-
‫ط‬=489216‫و‬=7‫ي‬=6
‫س‬=16‫ص‬=4892
‫س‬+‫ص‬=16+4892=4908
‫ص‬ ‫ي‬=6×4892=29352
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
29352-4908=24444

52. ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫التطبيق‬ ‫وبتكرار‬:-
‫ط‬=24444‫و‬=7‫ي‬=6
‫س‬=44‫ص‬=244
‫س‬+‫ص‬=44+244=288
‫ص‬ ‫ي‬=6×244=1464
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
1464-288=1176

53. ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫التطبيق‬ ‫وبتكرار‬:-
‫ط‬=1176‫و‬=7‫ي‬=6
‫س‬=76‫ص‬=11
‫س‬+‫ص‬=76+11=87
‫ص‬ ‫ي‬=6×11=66
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
66-87=‾21
‫العدد‬ ‫ان‬ ‫بما‬‾21=7×‾3
‫الطبيعي‬ ‫العدد‬ ‫اذن‬489216‫العدد‬ ‫مضاعفات‬7

54. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=489216‫ش‬=100002
‫م‬=216‫ن‬=489
‫م‬/=2‫ن‬/=100
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
100×216–2×489=
21600–987=20622

55. ‫التطبيق‬ ‫بتكرار‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬:-
‫ط‬=20622‫ش‬=10003
‫م‬=622‫ن‬=20
‫م‬/=3‫ن‬/=10
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
10×622–3×20=
6220–60=6160

56. ‫التطبيق‬ ‫بتكرار‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬:-
‫ط‬=6160‫ش‬=1001
‫م‬=60‫ن‬=61
‫م‬/=1‫ن‬/=10
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
10×60–1×61=
600–61=539

57. ‫التطبيق‬ ‫بتكرار‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬:-
‫ط‬=539‫ش‬=105
‫م‬=39‫ن‬=5
‫م‬/=5‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×39–5×5=
39–25=14
‫العدد‬ ‫ان‬ ‫بما‬14=7×2
‫العدد‬ ‫اذن‬489216‫العدد‬ ‫مضاعفات‬ ‫من‬7

58. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬11
‫مثال‬:-
‫اختبر‬‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬583‫االولي‬ ‫العدد‬ ‫على‬11:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=583‫و‬=11‫ي‬=0
‫س‬=83‫ص‬=5
‫س‬+‫ص‬=83+5=88
‫ص‬ ‫ي‬=0×5=0
0–88=‾88
‫العدد‬ ‫ان‬ ‫بما‬‾88=11×‾8
‫الطبيعي‬ ‫العدد‬ ‫اذن‬583‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬11

59. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=583‫ش‬=110
‫م‬=83‫ن‬=5
‫م‬/=10‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×83–10×5=
83–50=33
‫العدد‬ ‫ان‬ ‫بما‬33=11×3
‫الطبيعي‬ ‫العدد‬ ‫اذن‬583‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬11

60. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬13
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬819‫االولي‬ ‫العدد‬ ‫على‬13:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=819‫و‬=13‫ي‬=5
‫س‬=19‫ص‬=8
‫س‬+‫ص‬=19+8=27
‫ص‬ ‫ي‬=5×8=40
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
40–27=13
‫العدد‬ ‫ان‬ ‫بما‬13=13×1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬819‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬13

61. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=819‫ش‬=104
‫م‬=19‫ن‬=8
‫م‬/=4‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×19–4×8=
19–40=‾13
‫العدد‬ ‫ان‬ ‫بما‬‾13=13×‾1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬819‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬13

62. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬17
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬935‫االولي‬ ‫العدد‬ ‫على‬17:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=935‫و‬=17‫ي‬=3
‫س‬=35‫ص‬=9
‫س‬+‫ص‬=35+9=44
‫ص‬ ‫ي‬=3×9=27
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
27–44=‾17
‫العدد‬ ‫ان‬ ‫بما‬‾17=17×‾1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬935‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬17

63. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=935‫ش‬=102
‫م‬=35‫ن‬=9
‫م‬/=2‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×35–2×9=
35–18=17
‫العدد‬ ‫ان‬ ‫بما‬17=17×1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬935‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬17

64. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬19
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬741‫االولي‬ ‫العدد‬ ‫على‬19:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=741‫و‬=19‫ي‬=15
‫س‬=41‫ص‬=7
‫س‬+‫ص‬=41+7=48
‫ص‬ ‫ي‬=15×7=105
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
105–48=57
‫العدد‬ ‫ان‬ ‫بما‬57=19×3
‫الطبيعي‬ ‫العدد‬ ‫اذن‬741‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬19

65. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=741‫ش‬=114
‫م‬=41‫ن‬=7
‫م‬/=14‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×41–14×7=
41–98=‾57
‫العدد‬ ‫ان‬ ‫بما‬‾57=19×‾3
‫الطبيعي‬ ‫العدد‬ ‫اذن‬741‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬19

66. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬23
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬529‫االولي‬ ‫العدد‬ ‫على‬23:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=529‫و‬=23‫ي‬=16
‫س‬=29‫ص‬=5
‫س‬+‫ص‬=29+5=34
‫ص‬ ‫ي‬=16×5=80
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
80–34=46
‫العدد‬ ‫ان‬ ‫بما‬46=23×2
‫الطبيعي‬ ‫العدد‬ ‫اذن‬529‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬23

67. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=529‫ش‬=115
‫م‬=29‫ن‬=5
‫م‬/=15‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×29–15×5=
29–75=‾46
‫العدد‬ ‫ان‬ ‫بما‬‾46=23×‾2
‫الطبيعي‬ ‫العدد‬ ‫اذن‬529‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬23

68. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬29
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬348‫االولي‬ ‫العدد‬ ‫على‬29:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=348‫و‬=29‫ي‬=17
‫س‬=48‫ص‬=3
‫س‬+‫ص‬=48+3=51
‫ص‬ ‫ي‬=17×3=51
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
51–51=0
‫الطبيعي‬ ‫العدد‬ ‫اذن‬348‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬29

69. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=348‫ش‬=116
‫م‬=48‫ن‬=3
‫م‬/=16‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×48–16×3=
48–48=0
‫الطبيعي‬ ‫العدد‬ ‫اذن‬348‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬29

70. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬31
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬713‫االولي‬ ‫العدد‬ ‫على‬31:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=713‫و‬=31‫ي‬=25
‫س‬=13‫ص‬=7
‫س‬+‫ص‬=13+7=20
‫ص‬ ‫ي‬=25×7=175
175–20=155

71. ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫التطبيق‬ ‫وبتكرار‬:-
‫ط‬=155‫و‬=31‫ي‬=25
‫س‬=55‫ص‬=1
‫س‬+‫ص‬=55+1=56
‫ص‬ ‫ي‬=25×1=25
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
25-56=‾31
‫العدد‬ ‫ان‬ ‫بما‬‾31=31×‾1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬713‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬29

72. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=713‫ش‬=124
‫م‬=13‫ن‬=7
‫م‬/=24‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×13–24×7=
13–167=‾155

73. ‫التطبيق‬ ‫بتكرار‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬:-
‫ط‬=‾155‫ش‬=124
‫م‬=55‫ن‬=1
‫م‬/=24‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×55–24×1=
55–24=31
‫العدد‬ ‫ان‬ ‫بما‬31=31×1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬713‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬31

74. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬37
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬814‫االولي‬ ‫العدد‬ ‫على‬37:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=814‫و‬=37‫ي‬=12
‫س‬=14‫ص‬=8
‫س‬+‫ص‬=14+8=22
‫ص‬ ‫ي‬=12×8=96
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
96–22=74
‫العدد‬ ‫ان‬ ‫بما‬74=37×2
‫الطبيعي‬ ‫العدد‬ ‫اذن‬814‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬37

75. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=814‫ش‬=111
‫م‬=14‫ن‬=8
‫م‬/=11‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
×14–11×8=
14–88=‾74
‫العدد‬ ‫ان‬ ‫بما‬‾74=37×‾2
‫الطبيعي‬ ‫العدد‬ ‫اذن‬814‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬37

76. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬41
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬943‫االولي‬ ‫العدد‬ ‫على‬41:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=943‫و‬=41‫ي‬=24
‫س‬=43‫ص‬=9
‫س‬+‫ص‬=43+9=52
‫ص‬ ‫ي‬=24×9=216
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
216–52=164
‫العدد‬ ‫ان‬ ‫بما‬164=41×4
‫الطبيعي‬ ‫العدد‬ ‫اذن‬943‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬41

77. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=943‫ش‬=123
‫م‬=43‫ن‬=9
‫م‬/=23‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×43–24×9=
43–207=‾164
‫العدد‬ ‫ان‬ ‫بما‬‾164=41×‾4
‫الطبيعي‬ ‫العدد‬ ‫اذن‬943‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬41

78. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬43
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬817‫االولي‬ ‫العدد‬ ‫على‬43:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=817‫و‬=43‫ي‬=30
‫س‬=17‫ص‬=8
‫س‬+‫ص‬=17+8=25
‫ص‬ ‫ي‬=30×8=240
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
240–25=215
‫ان‬ ‫وبما‬215=43×5
‫الطبيعي‬ ‫العدد‬ ‫اذن‬817‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬43

79. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=817‫ش‬=129
‫م‬=17‫ن‬=8
‫م‬/=29‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×17–29×8=
17–232=‾215
‫العدد‬ ‫بما‬‾215=43×‾5
‫الطبيعي‬ ‫العدد‬ ‫اذن‬817‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬43
‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬47

80. ‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬423‫االولي‬ ‫العدد‬ ‫على‬47:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=423‫و‬=47‫ي‬=42
‫س‬=23‫ص‬=4
‫س‬+‫ص‬=23+4=27
‫ص‬ ‫ي‬=42×4=168
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
168–27=141
‫العدد‬ ‫ان‬ ‫بما‬141=47×3
‫الطبيعي‬ ‫العدد‬ ‫اذن‬423‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬47

81. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=423‫ش‬=141
‫م‬=23‫ن‬=4
‫م‬/=41‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×23–41×4=
23–164=‾141
‫العدد‬ ‫بما‬‾141=47×‾3
‫الطبيعي‬ ‫العدد‬ ‫اذن‬423‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬47

82. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬53
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬742‫االولي‬ ‫العدد‬ ‫على‬53:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=742‫و‬=53‫ي‬=7
‫س‬=42‫ص‬=7
‫س‬+‫ص‬=42+7=49
‫ص‬ ‫ي‬=7×7=49
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
49–49=0
‫الطبيعي‬ ‫العدد‬ ‫اذن‬742‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬53

83. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=742‫ش‬=106
‫م‬=42‫ن‬=7
‫م‬/=06‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×42–6×7=
42–42=0
‫الطبيعي‬ ‫العدد‬ ‫اذن‬742‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬53

84. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬59
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬413‫االولي‬ ‫العدد‬ ‫على‬59:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=413‫و‬=59‫ي‬=19
‫س‬=13‫ص‬=4
‫س‬+‫ص‬=13+4=17
‫ص‬ ‫ي‬=19×4=76
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
76–17=59
‫الطبيعي‬ ‫العدد‬ ‫اذن‬413‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬59

85. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=413‫ش‬=118
‫م‬=13‫ن‬=4
‫م‬/=18‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×13–18×4=
13–72=‾59
‫العدد‬ ‫ان‬ ‫بما‬‾59=59×‾1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬413‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬59

86. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬61
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬427‫االولي‬ ‫العدد‬ ‫على‬61:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=427‫و‬=61‫ي‬=23
‫س‬=27‫ص‬=4
‫س‬+‫ص‬=27+4=31
‫ص‬ ‫ي‬=23×4=92
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
92–31=61
‫الطبيعي‬ ‫العدد‬ ‫اذن‬427‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬61

87. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=427‫ش‬=122
‫م‬=27‫ن‬=4
‫م‬/=22‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×27–22×4=
27–88=‾61
‫العدد‬ ‫ان‬ ‫بما‬‾61=61×‾1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬427‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬61

88. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬67
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬536‫االولي‬ ‫العدد‬ ‫على‬67:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=536‫و‬=67‫ي‬=35
‫س‬=36‫ص‬=5
‫س‬+‫ص‬=36+5=41
‫ص‬ ‫ي‬=35×5=175
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
175–41=134
‫الطبيعي‬ ‫العدد‬ ‫ان‬ ‫بما‬536=67×2
‫الطبيعي‬ ‫العدد‬ ‫اذن‬536‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬67

89. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=536‫ش‬=134
‫م‬=36‫ن‬=5
‫م‬/=34‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×36–34×5=
36–170=‾134
‫العدد‬ ‫ان‬ ‫بما‬‾134=34×‾2
‫الطبيعي‬ ‫العدد‬ ‫اذن‬536‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬67

90. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬71
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬497‫االولي‬ ‫العدد‬ ‫على‬71:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=497‫و‬=71‫ي‬=43
‫س‬=97‫ص‬=4
‫س‬+‫ص‬=97+4=101
‫ص‬ ‫ي‬=43×4=172
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
172–101=71
‫الطبيعي‬ ‫العدد‬ ‫ان‬ ‫بما‬71=71×1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬497‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬71

91. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=497‫ش‬=142
‫م‬=97‫ن‬=4
‫م‬/=42‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×97–42×4=
97–168=‾71
‫العدد‬ ‫ان‬ ‫بما‬‾71=71×‾1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬497‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬71

92. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬73
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬292‫االولي‬ ‫العدد‬ ‫على‬73:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=292‫و‬=73‫ي‬=47
‫س‬=92‫ص‬=2
‫س‬+‫ص‬=92+2=94
‫ص‬ ‫ي‬=47×2=94
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
94–94=0‫الطبيعي‬ ‫العدد‬ ‫اذن‬292‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬73

93. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=292‫ش‬=146
‫م‬=92‫ن‬=2
‫م‬/=46‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×92–46×2=
92–92=0
‫الطبيعي‬ ‫العدد‬ ‫اذن‬292‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬73

94. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬79
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬237‫االولي‬ ‫العدد‬ ‫على‬79:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=237‫و‬=79‫ي‬=59
‫س‬=37‫ص‬=2
‫س‬+‫ص‬=37+2=39
‫ص‬ ‫ي‬=59×2=118
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
118–39=79
‫الطبيعي‬ ‫العدد‬ ‫اذن‬237‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬79


95. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=237‫ش‬=158
‫م‬=37‫ن‬=2
‫م‬/=58‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×37–58×2=
37–116=‾79
‫العدد‬ ‫ان‬ ‫بما‬‾79=79×‾1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬237‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬79

96. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬83
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬249‫االولي‬ ‫العدد‬ ‫على‬83:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=249‫و‬=83‫ي‬=67
‫س‬=49‫ص‬=2
‫س‬+‫ص‬=49+2=51
‫ص‬ ‫ي‬=67×2=134
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
134–51=83
‫الطبيعي‬ ‫العدد‬ ‫اذن‬249‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬83


97. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=249‫ش‬=166
‫م‬=49‫ن‬=2
‫م‬/=66‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×49–66×2=
49–132=‾83
‫العدد‬ ‫ان‬ ‫بما‬‾83=83×‾1
‫الطبيعي‬ ‫العدد‬ ‫اذن‬249‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬83

98. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬89
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬623‫االولي‬ ‫العدد‬ ‫على‬89:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=623‫و‬=89‫ي‬=79
‫س‬=23‫ص‬=6
‫س‬+‫ص‬=23+6=29
‫ص‬ ‫ي‬=79×6=474
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
474–29=445
‫العدد‬ ‫ان‬ ‫بما‬445=89×5
‫الطبيعي‬ ‫العدد‬ ‫اذن‬623‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬89


99. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=623‫ش‬=178
‫م‬=23‫ن‬=6
‫م‬/=78‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×23–78×6=
23–468=‾445
‫العدد‬ ‫ان‬ ‫بما‬‾445=89×‾5
‫الطبيعي‬ ‫العدد‬ ‫اذن‬623‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬89

100. ‫االولي‬ ‫العدد‬ ‫على‬ ‫الطبيعية‬ ‫االعداد‬ ‫قسمة‬ ‫قابلية‬ ‫الختبار‬ ‫أمثلة‬97
‫مثال‬:-
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬679‫االولي‬ ‫العدد‬ ‫على‬97:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=679‫و‬=97
‫ي‬=95
‫س‬=79‫ص‬=6
‫س‬+‫ص‬=79+6=85
‫ص‬ ‫ي‬=95×6=570
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
570–85=485
‫العدد‬ ‫ان‬ ‫بما‬485=97×5
‫الطبيعي‬ ‫العدد‬ ‫اذن‬679‫االولي‬ ‫العدد‬ ‫المضاعفات‬ ‫من‬97

101. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=679‫ش‬=194
‫م‬=79‫ن‬=6
‫م‬/=94‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×79–94×6=
79–564=‾485
‫العدد‬ ‫ان‬ ‫بما‬‾485=97×‾5
‫الطبيعي‬ ‫العدد‬ ‫اذن‬679‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬97

102. ‫مالحظة‬:-
‫من‬ ‫االقل‬ ‫االعداد‬ ‫جميع‬ ‫على‬ ‫القاعدتان‬ ‫تنطبق‬100‫اولية‬ ‫والغير‬ ‫االولية‬.
‫مثال‬:
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلة‬ ‫اختبر‬112‫العدد‬ ‫على‬14:-
‫الحل‬:-
ً‫ال‬‫او‬:‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=112‫و‬/=14‫ي‬=13
‫س‬=12‫ص‬=1
‫س‬+‫ص‬=12+1=13
‫ص‬ ‫ي‬=13×1=13
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )
13–13=0
‫الطبيعي‬ ‫العدد‬ ‫اذن‬112‫العدد‬ ‫المضاعفات‬ ‫من‬14

103. ً‫ا‬‫ثاني‬:‫العشري‬ ‫المضاعف‬ ‫طريقة‬ ‫باستخدام‬:-
‫ط‬=112‫ش‬=112
‫م‬=12‫ن‬=1
‫م‬/=12‫ن‬/=1
‫العكسي‬ ‫بالضرب‬:-
‫ن‬/‫م‬–‫م‬/‫ن‬=
1×12–12×1=
12–12=0
‫الطبيعي‬ ‫العدد‬ ‫اذن‬112‫االولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬14

105. ‫لية‬‫و‬‫األ‬ ‫األعداد‬ ‫على‬ ‫القسمة‬ ‫ناتج‬ ‫اجياد‬
‫عدد‬ ‫اي‬ ‫قسمة‬ ‫ناتج‬ ‫ايجاد‬ ‫يمكن‬(‫األولي‬ ‫العدد‬ ‫على‬ ‫القسمة‬ ‫يقبل‬)‫من‬ ‫أي‬ ‫على‬
‫األولية‬ ‫األعداد‬‫من‬(7–97)‫اآلتية‬ ‫بالطريقة‬:
‫توضيحي‬ ‫مثال‬:-
‫العدد‬ ‫قسمة‬ ‫ناتج‬ ‫اوجد‬427‫األولي‬ ‫العدد‬ ‫على‬7
ً‫ال‬‫أو‬:‫من‬ ‫الناتج‬ ‫نقسم‬ ‫ثم‬ ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫نستخدم‬‫المعادلة‬(‫ي‬‫ص‬–(‫س‬
+‫ص‬) )‫و‬ ‫على‬:
‫ط‬=427‫و‬=7‫ي‬=6
‫س‬=27‫ص‬=4
‫س‬+‫ص‬=27+4=31
‫ص‬ ‫ي‬=6×4=24
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )24–31=‾7
∴‾7÷7=‾1

106. ‫ثانيا‬:‫من‬ ‫اكبر‬ ‫عشري‬ ‫مضاعف‬ ‫اول‬ ‫قسمة‬ ‫ناتج‬ ‫نوجد‬100‫االولي‬ ‫للعدد‬
‫على‬‫األولي‬ ‫العدد‬(‫ت‬ ‫بالرمز‬ ً‫ا‬‫اصطالح‬ ‫له‬ ‫يرمز‬)
‫ت‬=105÷7=15
ً‫ا‬‫ثالث‬:‫ضرب‬ ‫حاصل‬ ‫نوجد‬(‫ص‬×‫ت‬: )
4×15=60

107. ً‫ا‬‫رابع‬:‫ص‬ ‫من‬ ‫القسمة‬ ‫قابلية‬ ‫تحقيق‬ ‫ناتج‬ ‫نطرح‬×‫ت‬:
‫ملحوظة‬:
‫ص‬ ‫ي‬ ‫كانت‬ ‫إذا‬>‫س‬+‫ت‬ ‫ص‬ ‫من‬ ‫نطرحه‬ ، ‫موجب‬ ‫الناتج‬ ‫أي‬ ‫ص‬.‫إذا‬
‫ص‬ ‫ي‬ ‫كانت‬<‫س‬+‫ت‬ ‫ص‬ ‫إلى‬ ‫نجمعه‬ ، ‫سالب‬ ‫الناتج‬ ‫أي‬ ‫ص‬.
‫ت‬ ‫ص‬=60
‫القسمة‬ ‫قابلية‬ ‫اختبار‬ ‫ناتج‬=‾1(‫ص‬ ‫ي‬ ‫ان‬ ‫أي‬ ‫سالب‬ ‫عدد‬<‫س‬+‫ص‬)
∴60–(‾1=)60+1=61
∴‫األولي‬ ‫العدد‬ ‫على‬ ‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫ناتج‬=61

108. ‫مثال‬(1:)
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبر‬893‫األولي‬ ‫العدد‬ ‫على‬19
‫الحل‬
‫األفقي‬ ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:
‫ط‬=893‫و‬=19‫ي‬=15
‫س‬=93‫ص‬=8
‫س‬+‫ص‬=93+8=101
‫ص‬ ‫ي‬=15×8=120
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )120–101=19
∵19÷19=1
∴‫الطبيعي‬ ‫العدد‬893‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬19

109. ‫القسمة‬ ‫ناتج‬ ‫ايجاد‬:
‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬19‫أكبرمن‬100=114
‫ت‬=114÷19=6
‫ت‬ ‫ص‬=8×6=48
‫القسمة‬ ‫قابلية‬ ‫اختبار‬ ‫ناتج‬=1
‫ت‬ ‫ص‬–‫القسمة‬ ‫اختبارقابلية‬ ‫ناتج‬=48–1=47
∴‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫ناتج‬893‫األولي‬ ‫العدد‬ ‫على‬19=47

110. ‫مثال‬(2:)
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبر‬946‫األولي‬ ‫العدد‬ ‫على‬43
‫الحل‬
‫األفقي‬ ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:
‫ط‬=946‫و‬=43‫ي‬=30
‫س‬=46‫ص‬=9
‫س‬+‫ص‬=46+9=55
‫ص‬ ‫ي‬=30×9=270
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )270–55=215
∵215÷43=5
∴‫الطبيعي‬ ‫العدد‬946‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬43

111. ‫القسمة‬ ‫ناتج‬ ‫ايجاد‬:
‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬43‫أكبرمن‬100=129
‫ت‬=129÷43=3
‫ت‬ ‫ص‬=9×3=27
‫القسمة‬ ‫قابلية‬ ‫اختبار‬ ‫ناتج‬=5
‫ت‬ ‫ص‬–‫القسمة‬ ‫اختبارقابلية‬ ‫ناتج‬=27–5=22
∴‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫ناتج‬946‫األولي‬ ‫العدد‬ ‫على‬43=22

112. ‫مثال‬(3:)
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبر‬8967‫األولي‬ ‫العدد‬ ‫على‬61
‫الحل‬
‫األفقي‬ ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:
‫ط‬=8967‫و‬=61‫ي‬=23
‫س‬=67‫ص‬=89
‫س‬+‫ص‬=67+89=156
‫ص‬ ‫ي‬=23×89=2047
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )2047–156=1891
∵1891÷61=31
∴‫الطبيعي‬ ‫العدد‬8967‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬61

113. ‫القسمة‬ ‫ناتج‬ ‫ايجاد‬:
‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬61‫أكبرمن‬100=122
‫ت‬=122÷61=2
‫ت‬ ‫ص‬=89×2=178
‫القسمة‬ ‫قابلية‬ ‫اختبار‬ ‫ناتج‬=31
‫ت‬ ‫ص‬–‫القسمة‬ ‫اختبارقابلية‬ ‫ناتج‬=178–31=147
∴‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫ناتج‬8967‫األولي‬ ‫العدد‬ ‫على‬61=147

114. ‫مثال‬(4:)
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبر‬46689‫األولي‬ ‫العدد‬ ‫على‬79
‫الحل‬
‫األفقي‬ ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:
‫ط‬=46689‫و‬=79‫ي‬=59
‫س‬=89‫ص‬=466
‫س‬+‫ص‬=89+466=555
‫ص‬ ‫ي‬=59×466=27494
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )27494–555=26939
∵26939÷79=341
∴‫الطبيعي‬ ‫العدد‬46689‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬79

115. ‫القسمة‬ ‫ناتج‬ ‫ايجاد‬:
‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬79‫أكبرمن‬100=158
‫ت‬=158÷79=2
‫ت‬ ‫ص‬=466×2=932
‫القسمة‬ ‫قابلية‬ ‫اختبار‬ ‫ناتج‬=341
‫ت‬ ‫ص‬–‫القسمة‬ ‫اختبارقابلية‬ ‫ناتج‬=932–341=591
∴‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫ناتج‬46689‫األولي‬ ‫العدد‬ ‫على‬79=5
91

116. ‫مثال‬(5:)
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبر‬438572‫األولي‬ ‫العدد‬ ‫على‬83
‫الحل‬
‫األفقي‬ ‫االختباري‬ ‫العامل‬ ‫طريقة‬ ‫باستخدام‬:
‫ط‬=438572‫و‬=83‫ي‬=67
‫س‬=72‫ص‬=4385
‫س‬+‫ص‬=72+4385=4457
‫ص‬ ‫ي‬=67×4385=293795
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )293795–4457=289338
∵289338÷83=3486
∴‫الطبيعي‬ ‫العدد‬438572‫األولي‬ ‫العدد‬ ‫مضاعفات‬ ‫من‬83

117. ‫القسمة‬ ‫ناتج‬ ‫ايجاد‬:
‫األولي‬ ‫للعدد‬ ‫مضاعف‬ ‫أول‬83‫أكبرمن‬100=166
‫ت‬=166÷83=2
‫ت‬ ‫ص‬=4385×2=8770
‫القسمة‬ ‫قابلية‬ ‫اختبار‬ ‫ناتج‬=3486
‫ت‬ ‫ص‬–‫اختبارقابليةالقسمة‬ ‫ناتج‬=8770–3486=5284
∴‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫ناتج‬438572‫األولي‬ ‫العدد‬ ‫على‬83=52
84

118. ‫ملحوظة‬:
‫أق‬ ‫االولية‬ ‫غير‬ ‫األعداد‬ ‫و‬ ‫األولية‬ ‫األعداد‬ ‫جميع‬ ‫تشمل‬ ‫اعاله‬ ‫المعادالت‬ ‫و‬ ‫التطبيقات‬‫من‬ ‫ل‬
100
‫مثال‬:
‫الطبيعي‬ ‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫اختبر‬888‫األولي‬ ‫غير‬ ‫العدد‬ ‫على‬74‫القسمة‬ ‫ناتج‬ ‫أوجد‬ ‫ثم‬
‫الحل‬
‫ط‬=888‫و‬= /74‫ي‬=49
‫س‬=88‫ص‬=8
‫س‬+‫ص‬=88+8=96
‫ص‬ ‫ي‬=49×8=392
‫ص‬ ‫ي‬–(‫س‬+‫ص‬= )392–96=296
296÷74=4
∴‫الطبيعي‬ ‫العدد‬888‫العدد‬ ‫مضاعفات‬ ‫من‬74

119. ‫القسمة‬ ‫ناتج‬ ‫ايجاد‬:
‫العدد‬ ‫مضاعفات‬ ‫أول‬74‫من‬ ‫أكبر‬100=148
‫ت‬=148÷74=2
‫ت‬ ‫ص‬=8×2=16
‫ت‬ ‫ص‬–‫القسمة‬ ‫قابلية‬ ‫ناتج‬=16–4=12
∴‫العدد‬ ‫قسمة‬ ‫قابلية‬ ‫ناتج‬888‫على‬74=12