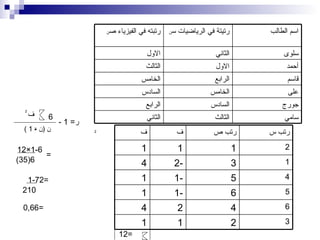
تناقش الوثيقة مفهوم الانتشار الإحصائي وعلاقته بالمتغيرات المستقلة والتابعة، وتعطي أمثلة على كيفية احتساب معامل الارتباط بيرسون وسكومن. تحتوي على معادلات لتحديد العلاقات بين المتغيرات وتأثير عدد أفراد الأسرة على استهلاك الماء. كما توضح كيفية استخدام البيانات لتحديد مدى الارتباط الإيجابي والسلبي بين المتغيرات.

1. أولاً : الانتشار : تعريف : شكل الانتشار هو الشكل الناتج من تعيين النقاط ( س 1 , ص 1 )( س 2 , ص 2 )_ _ _ ( س ن , ص ن ) للمتغيرين المستقل س والتابع ص حيث ( س 1 , ص 1 ) تمثل قيم المتغيرين للعنصر الأول في العينة ,( س 2 , ص 2 ) تمثل قيم المتغيرين للعنصر الثاني وهكذا . والشكل التالي سيوضح ذلك :- الاحصاء الارتباط

2. مثال : الجدول التالي يمثل عدد أفراد (10) اسر أخذت عشوائياً من احدى المدن الفلسطينية واستهلاك هذه الاسر شهرياً من الماء بالمتر المكعب . كمية استهلاك الماء ( ص ) 8 10 9 6 10 12 15 18 6 7 عدد أفراد الأسرة ( س ) 4 6 5 3 8 6 9 10 2 4 رقم الأسرة 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1 20 18 16 14 12 10 8 6 4 2 كمية الاستهلاك بالمتر المكعب ( ص ) عدد أفراد الأسرة ( س )

3. س س س س ص ص ص ص ارتباط ( خطي ايجابي ) ارتباط ( خطي سلبي ) لا يوجد ارتباط خطي ارتباط خطي ايجابي تام

4. ثانياً : معامل الارتباط الخطي : ص ص ص س س س ارتباط سلبي غير خطي ارتباط ايجابي ارتباط غير خطي ارتباط خطي سلبي تام ص حيث : س = الوسط الحسابي للمتغير س : س = 1- معامل ارتباط بيرسون :- هناك قانونان لمعامل الارتباط بيرسون هي : ر = س ص – ن س ص س - ن س 2 2 ص - ن ص 2 2 س ن ص = الوسط الحسابي للمتغير ص : ص = ن

5. مثال : احسب معامل ارتباط بيرسون بين المتغيرين س , ص واللذان يمثلان درجة الحرارة في خمسة أيام من شهر كانون الثاني في احدى السنوات في مدينتي رام الله والقدس علا الترتيب . الحل : نكون الجدول التالي : 2 2 2 2 القدس ( ص ) 2 -1 3 5 6 رام الله ( س ) -3 0 4 8 11 اليوم 3/12 4/12 5/12 6/12 7/12 س =20 ص =15 س =210 ص =75 س ص =12 11 6 121 36 66 8 5 64 25 40 4 3 16 9 12 0 -1 0 1 0 -3 2 9 4 -6 س ص س ص س ص

6. الوسط الحسابي للمتغير س : س = = 4 20 5 الوسط الحسابي للمتغير ص : ص = =3 15 5 س ص – ن س ص ر = 210-5×4 75-5×3 2 2 112-5×4×3 س - ن س 2 2 ص - ن ص 2 2 = = 130 30 52 52 3900 =

7. صورة اخرى لمعامل الارتباط بيرسون : احسب معامل ارتباط بيرسون بين المتغيرين س , ص باستخدام الصورة أعلاه . ( س - س ) ( ص - ص ) ( س - س ) ( ص - ص ) 2 2 ر = ص 4 2 3 2 4 س -2 3 4 2 3 نحسب س , ص : 10 5 س = =2 ص = =3 15 5

8. 2 2 =-0,46 س = 10 ص =15 =-4 =22 =4 3 4 2 1 1 1 1 2 2 0 -1 0 0 1 4 3 2 0 0 4 0 3 2 1 -1 -1 1 1 -2 4 -4 1 -4 16 1 س ص ( س - س ) ( ص _ ص ) ( س - س )( ص - ص ) ( س - س ) ( ص - ص ) ( س - س ) ( ص - ص ) ( س - س ) ( ص - ص ) 2 2 ر = 22 22 -2 = 22 4 -4 =

9. 2- معامل ارتباط سبيرمان ( الرتب ): حيث ف هي الفرق بين رتب المتغيرين المتناظرين , ن حجم العينه . مثال : احسب معامل الارتباط سبيرمان كانت رتب علامات 5 طلاب في امتحان الرياضيات والفيزياء ر = 1 - 6 ف ن ( ن - 1 ) 2 2

10. 2 = =0,66 سامي الثالث الثاني جورج السادس الرابع على الخامس السادس قاسم الرابع الخامس أحمد الاول الثالث سلوى الثاني الاول اسم الطالب رتيتة في الرياضيات س ن رتبته في الفيزياء ص ن 3 2 1 1 6 4 2 4 5 6 -1 1 4 5 -1 1 1 3 -2 4 2 1 1 1 رتب س رتب ص ف ف =12 1-6×12 6(35) =1-72 210 ر = 1 - 6 ف ن ( ن - 1 ) 2 2