Lesson 16: Inverse Trigonometric Functions

Section 3.5
Inverse Trigonometric
Functions
V63.0121.002.2010Su, Calculus I

New York University

June 7, 2010

Announcements

Exams not graded yet
Written HW due tomorrow
Quiz 3 on Thursday covering 3.3, 3.4, 3.5, 3.7

Announcements

Exams not graded yet
Written HW due tomorrow
Quiz 3 on Thursday covering
3.3, 3.4, 3.5, 3.7

V63.0121.002.2010Su, Calculus I (NYU) Section 3.5 Inverse Trigonometric Functions June 7, 2010 2 / 30

Objectives

Know the deﬁnitions,
domains, ranges, and other
properties of the inverse
trignometric functions:
arcsin, arccos, arctan,
arcsec, arccsc, arccot.
Know the derivatives of the
inverse trignometric
functions.


What is an inverse function?

Deﬁnition
Let f be a function with domain D and range E . The inverse of f is the
function f −1 deﬁned by:
f −1 (b) = a,
where a is chosen so that f (a) = b.


What is an inverse function?

Deﬁnition
Let f be a function with domain D and range E . The inverse of f is the
function f −1 deﬁned by:
f −1 (b) = a,
where a is chosen so that f (a) = b.

So
f −1 (f (x)) = x, f (f −1 (x)) = x


What functions are invertible?

In order for f −1 to be a function, there must be only one a in D
corresponding to each b in E .
Such a function is called one-to-one
The graph of such a function passes the horizontal line test: any
horizontal line intersects the graph in exactly one point if at all.
If f is continuous, then f −1 is continuous.


Outline

Inverse Trigonometric Functions

Derivatives of Inverse Trigonometric Functions
Arcsine
Arccosine
Arctangent
Arcsecant

Applications


arcsin

Arcsin is the inverse of the sine function after restriction to [−π/2, π/2].
y

x
π π sin
−
2 2


arcsin

y
y =x

x
π π sin
−
2 2


arcsin

y
arcsin

x
π π sin
−
2 2

The domain of arcsin is [−1, 1]
π π
The range of arcsin is − ,
2 2


arccos

Arccos is the inverse of the cosine function after restriction to [0, π]

y

cos
x
0 π


arccos


y
y =x

cos
x
0 π


arccos

arccos
y

cos
x
0 π

The domain of arccos is [−1, 1]
The range of arccos is [0, π]


arctan

Arctan is the inverse of the tangent yfunction after restriction to [−π/2, π/2].

x
3π π π 3π
− −
2 2 2 2

tan


arctan
y =x

x
3π π π 3π
− −
2 2 2 2

tan


arctan


π
2 arctan

x

π
−
2

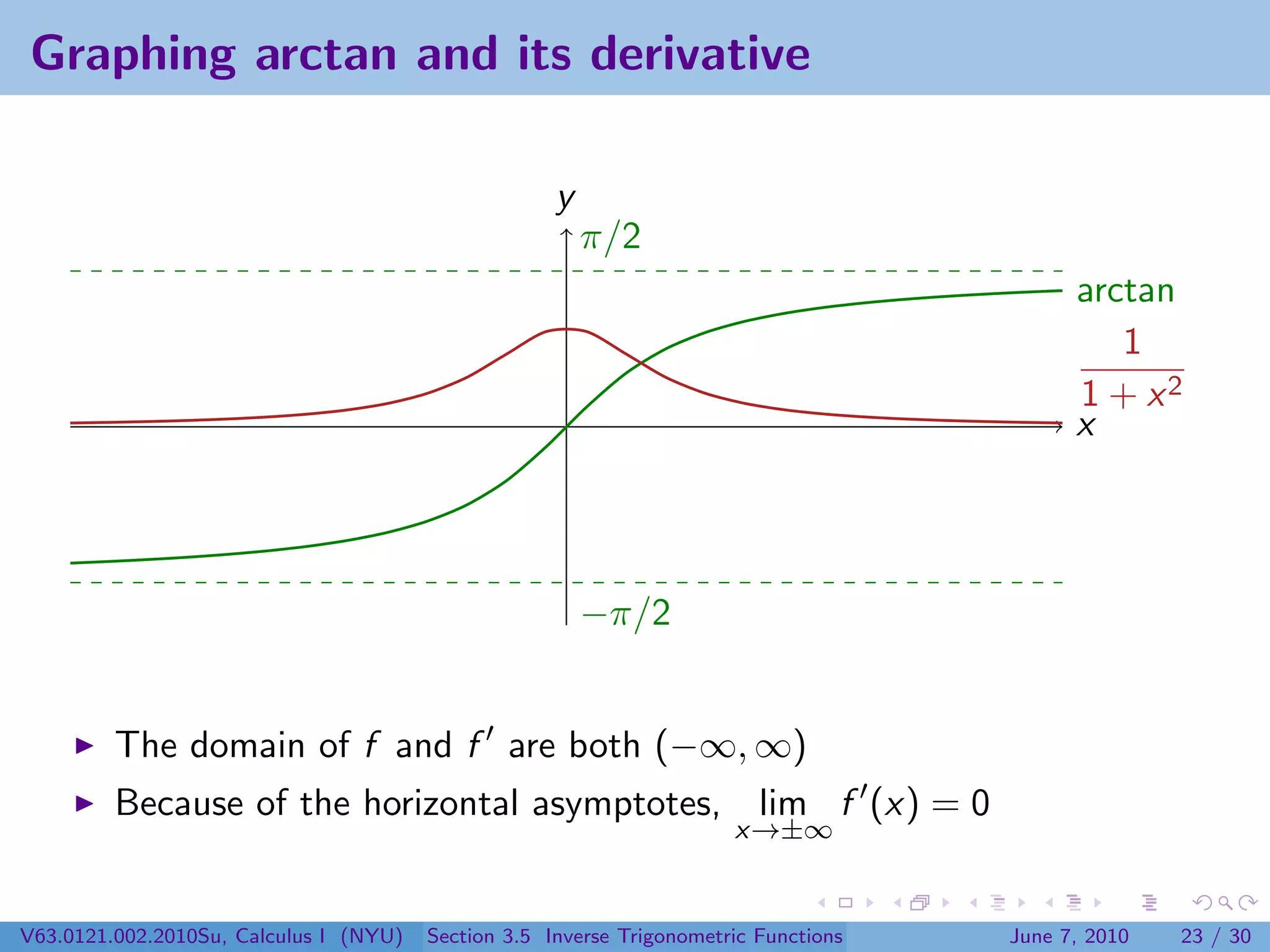
The domain of arctan is (−∞, ∞)
π π
The range of arctan is − ,
2 2
π π
lim arctan x = , lim arctan x = −
x→∞ 2 x→−∞ 2


arcsec
y
Arcsecant is the inverse of secant after restriction to [0, π/2) ∪ (π, 3π/2].

x
3π π π 3π
− −
2 2 2 2

sec


arcsec
y =x
y restriction to [0, π/2) ∪ (π, 3π/2].
Arcsecant is the inverse of secant after

x
3π π π 3π
− −
2 2 2 2

sec


3π
arcsec
2
y
Arcsecant is the inverse of secant after restriction to [0, π/2) ∪ (π, 3π/2].

π
2

x

The domain of arcsec is (−∞, −1] ∪ [1, ∞)
π π
The range of arcsec is 0, ∪ ,π
2 2
π 3π
lim arcsec x = , lim arcsec x =
x→∞ 2 x→−∞ 2


Values of Trigonometric Functions

π π π π
x 0
6 4 3 2
√ √
1 2 3
sin x 0 1
2 2 2
√ √
3 2 1
cos x 1 0
2 2 2
1 √
tan x 0 √ 1 3 undef
3
√ 1
cot x undef 3 1 √ 0
3
2 2
sec x 1 √ √ 2 undef
3 2
2 2
csc x undef 2 √ √ 1
2 3

Check: Values of inverse trigonometric functions
Example
Find
arcsin(1/2)
arctan(−1)
√
2
arccos −
2


Example
Find
arcsin(1/2)
arctan(−1)
√
2
arccos −
2

Solution
π
6


What is arctan(−1)?

3π/4

−π/4



3π/4 3π
Yes, tan = −1
4
√
2
sin(3π/4) =
2

√
2
cos(3π/4) = −
2

−π/4



3π/4 3π
Yes, tan = −1
4
√ But, the range of arctan is
2 π π
sin(3π/4) = − ,
2 2 2
√
2
cos(3π/4) = −
2

−π/4



3π/4 3π
Yes, tan = −1
4
But, the range of arctan is
√ π π
2 − ,
cos(π/4) = 2 2
2 Another angle whose
π
tangent is −1 is − , and
√ 4
2 this is in the right range.
sin(π/4) = −
2

−π/4



3π/4 3π
Yes, tan = −1
4
But, the range of arctan is
√ π π
2 − ,
cos(π/4) = 2 2
2 Another angle whose
π
tangent is −1 is − , and
√ 4
2 this is in the right range.
sin(π/4) = − π
2 So arctan(−1) = −
4
−π/4


Example
Find
arcsin(1/2)
arctan(−1)
√
2
arccos −
2

Solution
π
6
π
−
4


Example
Find
arcsin(1/2)
arctan(−1)
√
2
arccos −
2

Solution
π
6
π
−
4
3π
4


Caution: Notational ambiguity

sin2 x = (sin x)2 sin−1 x = (sin x)−1

sinn x means the nth power of sin x, except when n = −1!
The book uses sin−1 x for the inverse of sin x, and never for (sin x)−1 .
1
I use csc x for and arcsin x for the inverse of sin x.
sin x


Outline


Arcsine
Arccosine
Arctangent
Arcsecant

Applications


The Inverse Function Theorem

Theorem (The Inverse Function Theorem)
Let f be diﬀerentiable at a, and f (a) = 0. Then f −1 is deﬁned in an open
interval containing b = f (a), and

1
(f −1 ) (b) =
f (f −1 (b))


The Inverse Function Theorem

Theorem (The Inverse Function Theorem)
Let f be differentiable at a, and f (a) = 0. Then f −1 is defined in an open
interval containing b = f (a), and

1
(f −1 ) (b) =
f (f −1 (b))

Upshot: Many times the derivative of f −1 (x) can be found by implicit
differentiation and the derivative of f :


Derivation: The derivative of arcsin

Let y = arcsin x, so x = sin y . Then
dy dy 1 1
cos y = 1 =⇒ = =
dx dx cos y cos(arcsin x)



dy dy 1 1
cos y = 1 =⇒ = =

To simplify, look at a right
triangle:



dy dy 1 1
cos y = 1 =⇒ = =

triangle:

1
x



dy dy 1 1
cos y = 1 =⇒ = =

triangle:

1
x

y = arcsin x



dy dy 1 1
cos y = 1 =⇒ = =

triangle:

1
x

y = arcsin x

1 − x2



dy dy 1 1
cos y = 1 =⇒ = =

triangle:

cos(arcsin x) = 1 − x2 1
x

y = arcsin x

1 − x2



dy dy 1 1
cos y = 1 =⇒ = =

triangle:

cos(arcsin x) = 1 − x2 1
x
So
d 1
arcsin(x) = √ y = arcsin x
dx 1 − x2
1 − x2


Graphing arcsin and its derivative

1
√
1 − x2
The domain of f is [−1, 1],
but the domain of f is arcsin
(−1, 1)
lim f (x) = +∞
x→1−
| |
lim f (x) = +∞ −1 1
x→−1+


Derivation: The derivative of arccos

Let y = arccos x, so x = cos y . Then
dy dy 1 1
− sin y = 1 =⇒ = =
dx dx − sin y − sin(arccos x)


Derivation: The derivative of arccos

Let y = arccos x, so x = cos y . Then
dy dy 1 1
− sin y = 1 =⇒ = =
dx dx − sin y − sin(arccos x)

triangle:

sin(arccos x) = 1 − x2 1
1 − x2
So
d 1 y = arccos x
arccos(x) = − √
dx 1 − x2 x


Graphing arcsin and arccos

arccos

arcsin

| |
−1 1


Graphing arcsin and arccos

arccos
Note
π
arcsin cos θ = sin −θ
2
π
=⇒ arccos x = − arcsin x
2
| |
−1 1 So it’s not a surprise that their
derivatives are opposites.


Derivation: The derivative of arctan

Let y = arctan x, so x = tan y . Then
dy dy 1
sec2 y = 1 =⇒ = = cos2 (arctan x)
dx dx sec2 y



dy dy 1
dx dx sec2 y

triangle:



dy dy 1
dx dx sec2 y

triangle:

x

1



dy dy 1
dx dx sec2 y

triangle:

x

y = arctan x
1



dy dy 1
dx dx sec2 y

triangle:

1 + x2 x

y = arctan x
1



dy dy 1
dx dx sec2 y

triangle:
1
cos(arctan x) = √
1 + x2
1 + x2 x

y = arctan x
1



dy dy 1
dx dx sec2 y

triangle:
1
cos(arctan x) = √
1 + x2
1 + x2 x
So
d 1
arctan(x) = y = arctan x
dx 1 + x2
1


Graphing arctan and its derivative

y
π/2
arctan
1
1 + x2
x

−π/2

The domain of f and f are both (−∞, ∞)
Because of the horizontal asymptotes, lim f (x) = 0
x→±∞


Example
√
Let f (x) = arctan x. Find f (x).


Example
√
Let f (x) = arctan x. Find f (x).

Solution

d √ 1 d √ 1 1
dx
arctan x = √ 2 dx x = 1 + x · 2√x
1+ x
1
= √ √
2 x + 2x x


Derivation: The derivative of arcsec

Try this ﬁrst.



Try this ﬁrst. Let y = arcsec x, so x = sec y . Then
dy dy 1 1
sec y tan y = 1 =⇒ = =
dx dx sec y tan y x tan(arcsec(x))



dy dy 1 1
sec y tan y = 1 =⇒ = =

triangle:



dy dy 1 1
sec y tan y = 1 =⇒ = =

triangle:

x

1



dy dy 1 1
sec y tan y = 1 =⇒ = =

triangle:

x

y = arcsec x
1



dy dy 1 1
sec y tan y = 1 =⇒ = =

triangle:
√
x2 − 1
tan(arcsec x) =
1
x x2 − 1

y = arcsec x
1



dy dy 1 1
sec y tan y = 1 =⇒ = =

triangle:
√
x2 − 1
tan(arcsec x) =
1
x x2 − 1
So
d 1
arcsec(x) = √ y = arcsec x
dx x x2 − 1
1


Another Example

Example
Let f (x) = e arcsec x . Find f (x).


Another Example

Example
Let f (x) = e arcsec x . Find f (x).

Solution

1
f (x) = e arcsec x · √
x x2 − 1


Outline


Arcsine
Arccosine
Arctangent
Arcsecant

Applications


Application

Example

One of the guiding principles of
most sports is to “keep your eye
on the ball.” In baseball, a batter
stands 2 ft away from home plate
as a pitch is thrown with a
velocity of 130 ft/sec (about
90 mph). At what rate does the
batter’s angle of gaze need to
change to follow the ball as it
crosses home plate?


Solution
Let y (t) be the distance from the ball to home plate, and θ the angle the
batter’s eyes make with home plate while following the ball. We know
y = −130 and we want θ at the moment that y = 0.

y

130 ft/sec

θ
2 ft


Solution
We have θ = arctan(y /2). Thus

dθ 1 1 dy
= ·
dt 1 + (y /2)2 2 dt

y

130 ft/sec

θ
2 ft


Solution

dθ 1 1 dy
= ·
dt 1 + (y /2)2 2 dt

When y = 0 and y = −130,
then y

dθ 1 1
= · (−130) = −65 rad/sec 130 ft/sec
dt y =0 1+0 2
θ
2 ft


Solution

dθ 1 1 dy
= ·
dt 1 + (y /2)2 2 dt

When y = 0 and y = −130,
then y

dθ 1 1
= · (−130) = −65 rad/sec 130 ft/sec
dt y =0 1+0 2

The human eye can only track θ
at 3 rad/sec! 2 ft


Summary

y y

1
arcsin x √
1 − x2
1
arccos x −√
1 − x2 Remarkable that the
1 derivatives of these
arctan x transcendental functions are
1 + x2
1 algebraic (or even rational!)
arccot x −
1 + x2
1
arcsec x √
x x2 − 1
1
arccsc x − √
x x2 − 1

Lesson 16: Inverse Trigonometric Functions

More Related Content

What's hot

Viewers also liked

Similar to Lesson 16: Inverse Trigonometric Functions

More from Matthew Leingang

Recently uploaded

Lesson 16: Inverse Trigonometric Functions