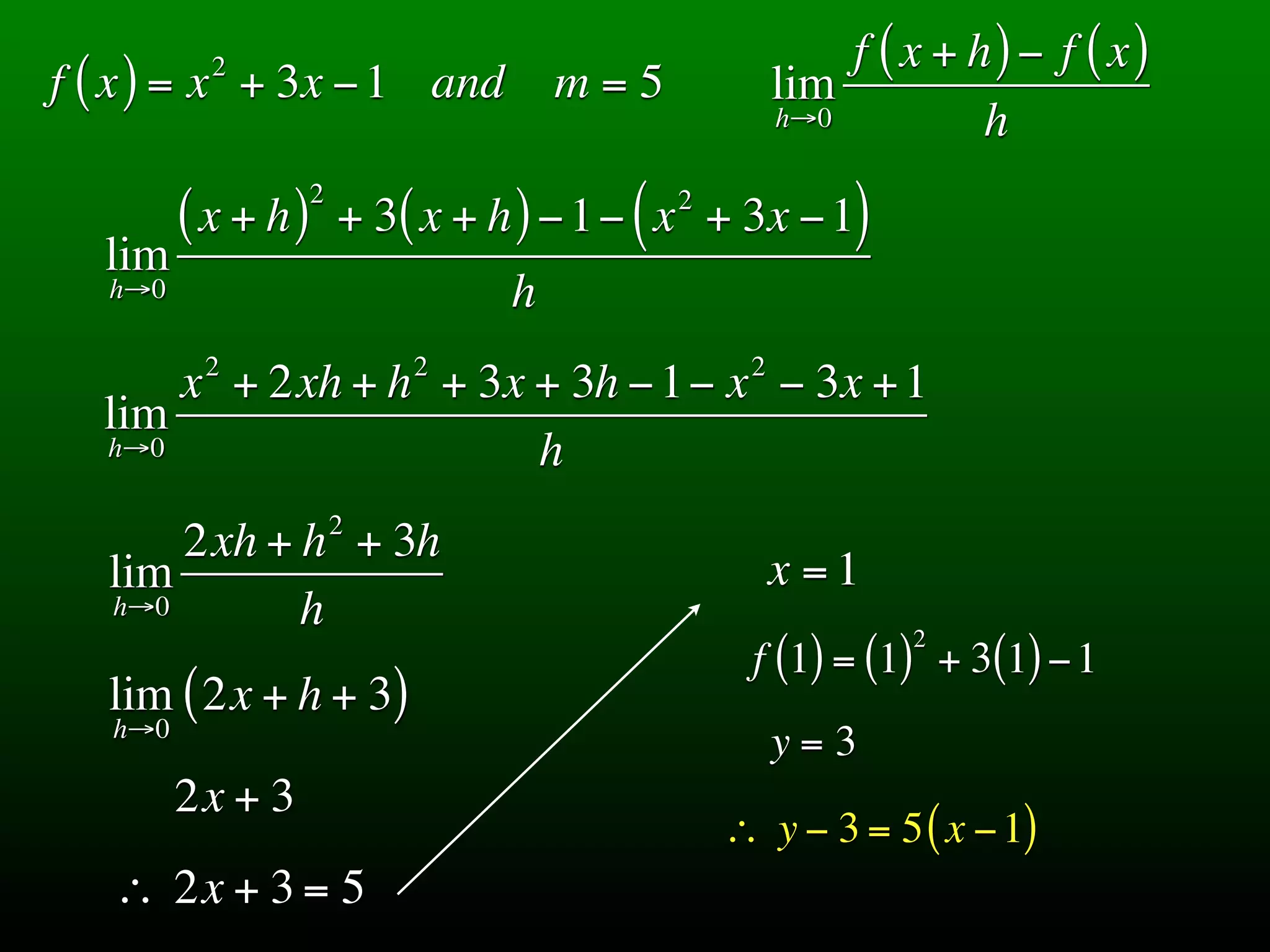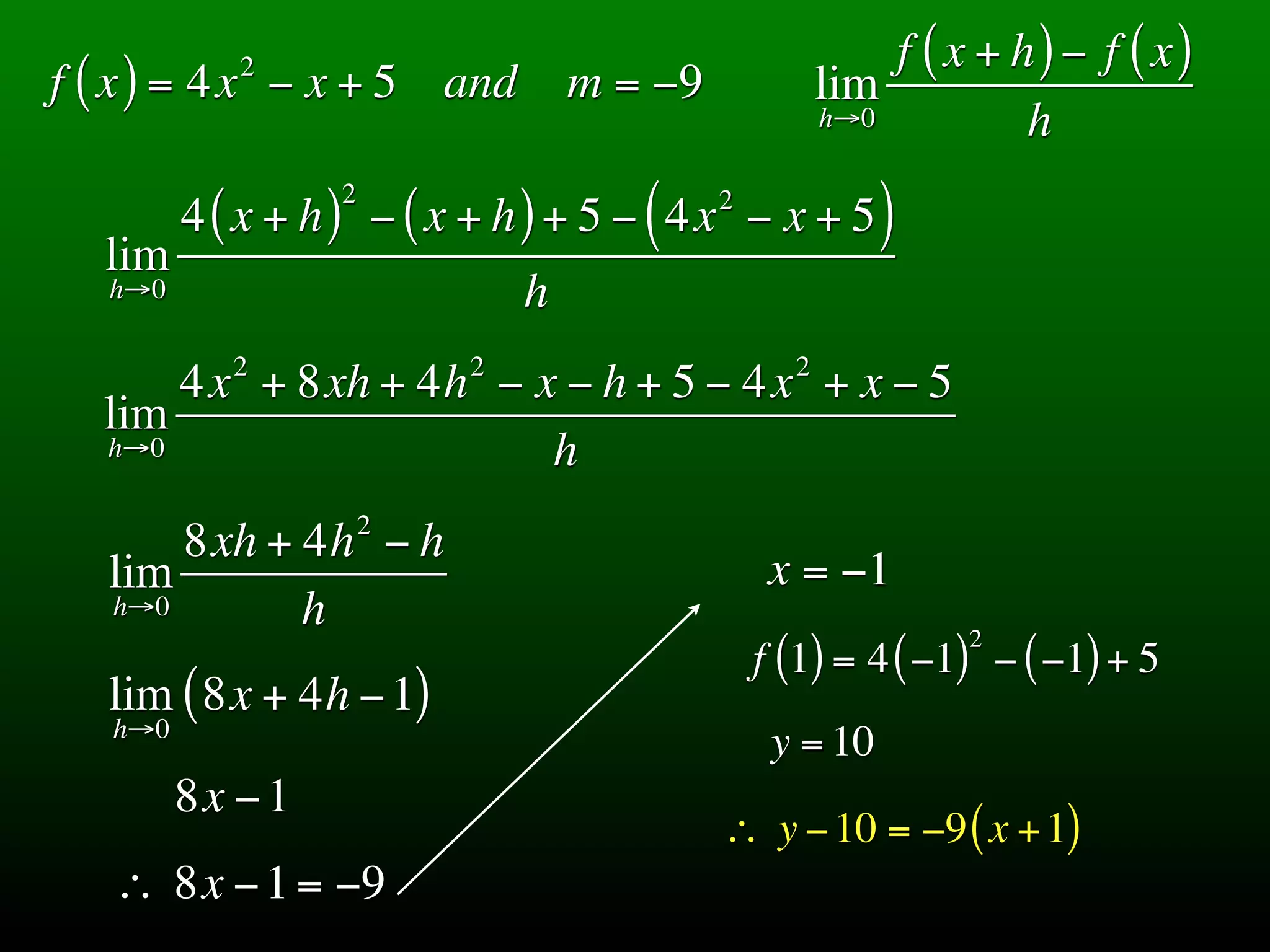The document discusses tangent lines to functions. It provides examples of finding the equation of a tangent line with a given slope to specific functions. It also discusses finding the average and instantaneous velocity of an object given its position function.

1. 12.3 Tangent to a Curve
Day Two
Colossians 3:17 “And whatever you do, in word or deed, do
everything in the name of the Lord Jesus, giving thanks
to God the Father through him.”

2. Find the equation of the line with slope
of 5 that is tangent to the graph of
2
f ( x ) = x + 3x − 1 I’ll do this on the board

3. Find the equation of the line with slope
of 5 that is tangent to the graph of
2
f ( x ) = x + 3x − 1 I’ll do this on the board
The slope of the tangent line is also the value of the
derivative of the function at that point. I’ll find the general
derivative of the function and set that equal to 5 in order
to find the x-value. From that I can then find the
corresponding y-value. Point-Slope form is then easy to
produce.

4. 2 f ( x + h) − f ( x)
f ( x ) = x + 3x − 1 and m=5 lim
h→0 h
2
( x + h) + 3( x + h ) − 1− ( x + 3x − 1)
2
lim
h→0 h
2 2 2
x + 2xh + h + 3x + 3h − 1− x − 3x + 1
lim
h→0 h
2
2xh + h + 3h
lim x =1
h→0 h 2
f (1) = (1) + 3(1) − 1
lim ( 2x + h + 3)
h→0
y=3
2x + 3
∴ y − 3 = 5 ( x − 1)
∴ 2x + 3 = 5

5. Groups: Find the equation of the line
with slope of -9 that is tangent to the
function f ( x ) = 4x − x + 5
2

6. 2 f ( x + h) − f ( x)
f ( x ) = 4x − x + 5 and m = −9 lim
h→0 h
2
4 ( x + h ) − ( x + h ) + 5 − ( 4x − x + 5 )
2
lim
h→0 h
2 2 2
4x + 8xh + 4h − x − h + 5 − 4x + x − 5
lim
h→0 h
2
8xh + 4h − h
lim x = −1
h→0 h 2
f (1) = 4 ( −1) − ( −1) + 5
lim ( 8x + 4h − 1)
h→0
y = 10
8x − 1
∴ y − 10 = −9 ( x + 1)
∴ 8x − 1 = −9

7. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
1. What is the average velocity of the object between
t=2 and t=4 seconds?

8. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
1. What is the average velocity of the object between
t=2 and t=4 seconds?
t f(t)
2 3
4 9

9. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
1. What is the average velocity of the object between
t=2 and t=4 seconds?
t f(t)
Δy 9 − 3
= = 3 ft s
2 3 Δx 4 − 2
4 9

10. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?

11. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?
f (t + h ) − f (t )
lim
h→0 h

12. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?
f (t + h ) − f (t )
lim
h→0 h
2
(t + h ) − 3( t + h ) + 5 − ( t − 3t + 5 )
2
lim
h→0 h

13. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?
f (t + h ) − f (t )
lim
h→0 h
2
(t + h ) − 3( t + h ) + 5 − ( t − 3t + 5 )
2
lim
h→0 h
2 2 2
t + 2th + h − 3t − 3h + 5 − t + 3t − 5
lim
h→0 h

14. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?
f (t + h ) − f (t )
lim
h→0 h
2
(t + h ) − 3( t + h ) + 5 − ( t − 3t + 5 )
2
lim
h→0 h
2 2 2
t + 2th + h − 3t − 3h + 5 − t + 3t − 5
lim
h→0 h
2
2th + h − 3h
lim
h→0 h

15. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?
f (t + h ) − f (t ) lim ( 2t + h − 3)
lim h→0
h→0 h
2
(t + h ) − 3( t + h ) + 5 − ( t − 3t + 5 )
2
lim
h→0 h
2 2 2
t + 2th + h − 3t − 3h + 5 − t + 3t − 5
lim
h→0 h
2
2th + h − 3h
lim
h→0 h

16. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?
f (t + h ) − f (t ) lim ( 2t + h − 3)
lim h→0
h→0 h
2t − 3
2
(t + h ) − 3( t + h ) + 5 − ( t − 3t + 5 )
2
lim
h→0 h
2 2 2
t + 2th + h − 3t − 3h + 5 − t + 3t − 5
lim
h→0 h
2
2th + h − 3h
lim
h→0 h

17. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?
f (t + h ) − f (t ) lim ( 2t + h − 3)
lim h→0
h→0 h
2t − 3
2
(t + h ) − 3( t + h ) + 5 − ( t − 3t + 5 )
2
lim at t = 2.5
h→0 h
m = 2 ( 2.5 ) − 3 = 2
2 2 2
t + 2th + h − 3t − 3h + 5 − t + 3t − 5
lim
h→0 h
2
2th + h − 3h
lim
h→0 h

18. The motion of an object is given by the function,
f ( t ) = t − 3t + 5 , where f ( t ) is the height of the
2
object in feet at time t seconds.
2. What is the instantaneous velocity of the object at
t=2.5 seconds?
f (t + h ) − f (t ) lim ( 2t + h − 3)
lim h→0
h→0 h
2t − 3
2
(t + h ) − 3( t + h ) + 5 − ( t − 3t + 5 )
2
lim at t = 2.5
h→0 h
m = 2 ( 2.5 ) − 3 = 2
2 2 2
t + 2th + h − 3t − 3h + 5 − t + 3t − 5
lim
h→0 h ∴ 2 ft s
2
2th + h − 3h
lim
h→0 h

19. HW #4
“Whatever you are, be a good one.”
Abraham Lincoln