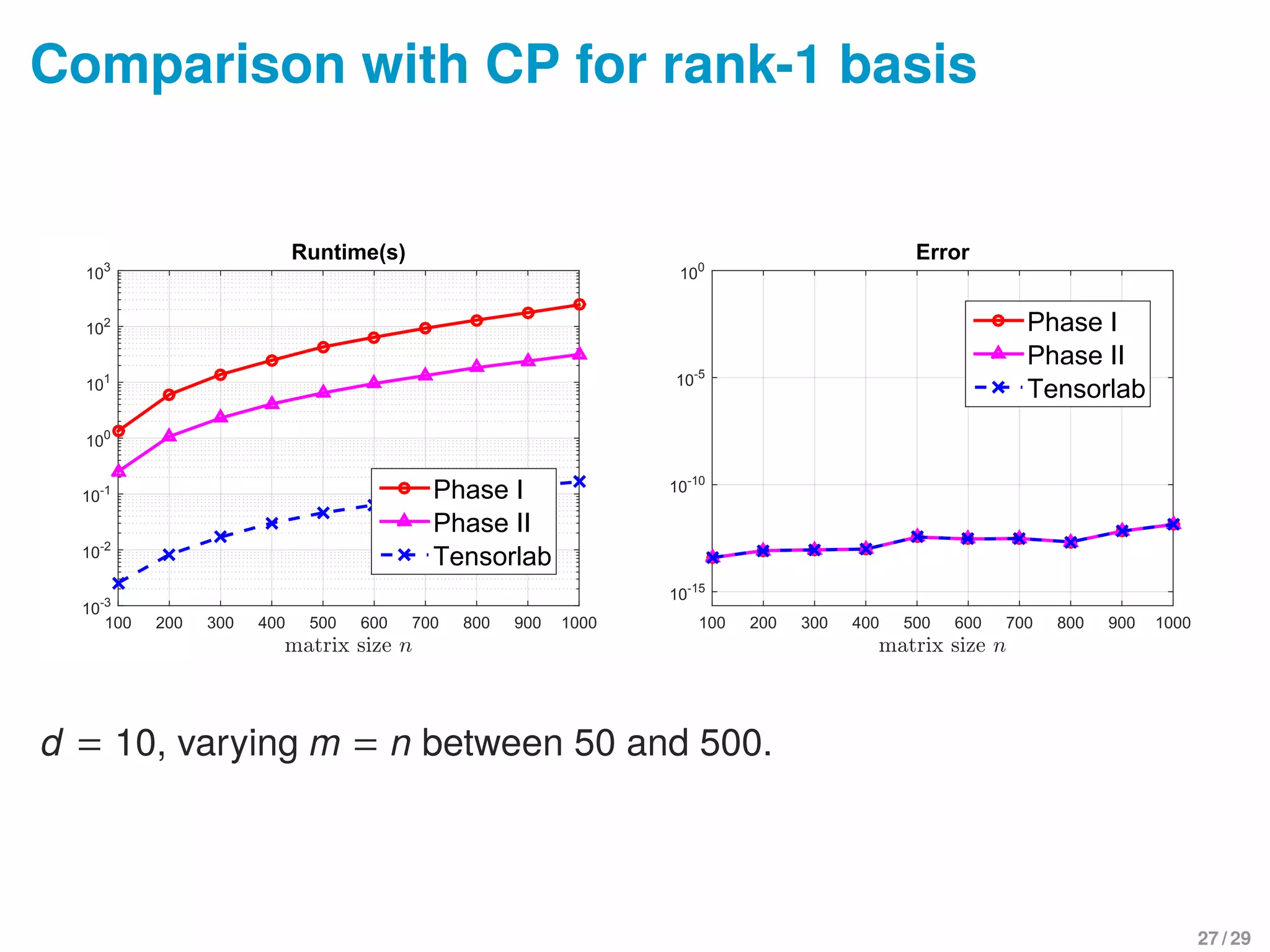
This document summarizes a presentation on finding low-rank bases for matrix subspaces. It introduces the low-rank basis problem, describes a greedy algorithm to solve it using two phases - rank estimation and alternating projection, and proves local convergence guarantees for the algorithm. Experimental results on synthetic and image data demonstrate the algorithm can recover known low-rank bases and separate mixed images. Comparisons are made to tensor decomposition methods for the special case of rank-1 bases.

1. The low-rank basis problem
for a matrix subspace
Tasuku Soma
Univ. Tokyo
Joint work with:
Yuji Nakatsukasa (Univ. Tokyo)
André Uschmajew (Univ. Bonn)
1 / 29

2. 1 The low-rank basis problem
2 Algorithm
3 Convergence Guarantee
4 Experiments
2 / 29

3. 1 The low-rank basis problem
2 Algorithm
3 Convergence Guarantee
4 Experiments
3 / 29

4. The low-rank basis problem
Low-rank basis problem: for a matrix subspace M ⊆ Rm×n
spanned
by M1,. . . ,Md ∈ Rm×n
,
minimize rank(X1) + · · · + rank(Xd )
subject to span{X1,. . . ,Xd } = M.
4 / 29

5. The low-rank basis problem
Low-rank basis problem: for a matrix subspace M ⊆ Rm×n
spanned
by M1,. . . ,Md ∈ Rm×n
,
minimize rank(X1) + · · · + rank(Xd )
subject to span{X1,. . . ,Xd } = M.
• Generalizes the sparse basis problem:
minimize x1 0 + · · · + xd 0
subject to span{x1,. . . ,xd } = S ⊆ RN
.
• Matrix singular values play role of vector nonzero elements
4 / 29

6. Scope
lowrank basis
sparse basis
(Coleman-Pothen 86)
basis problems

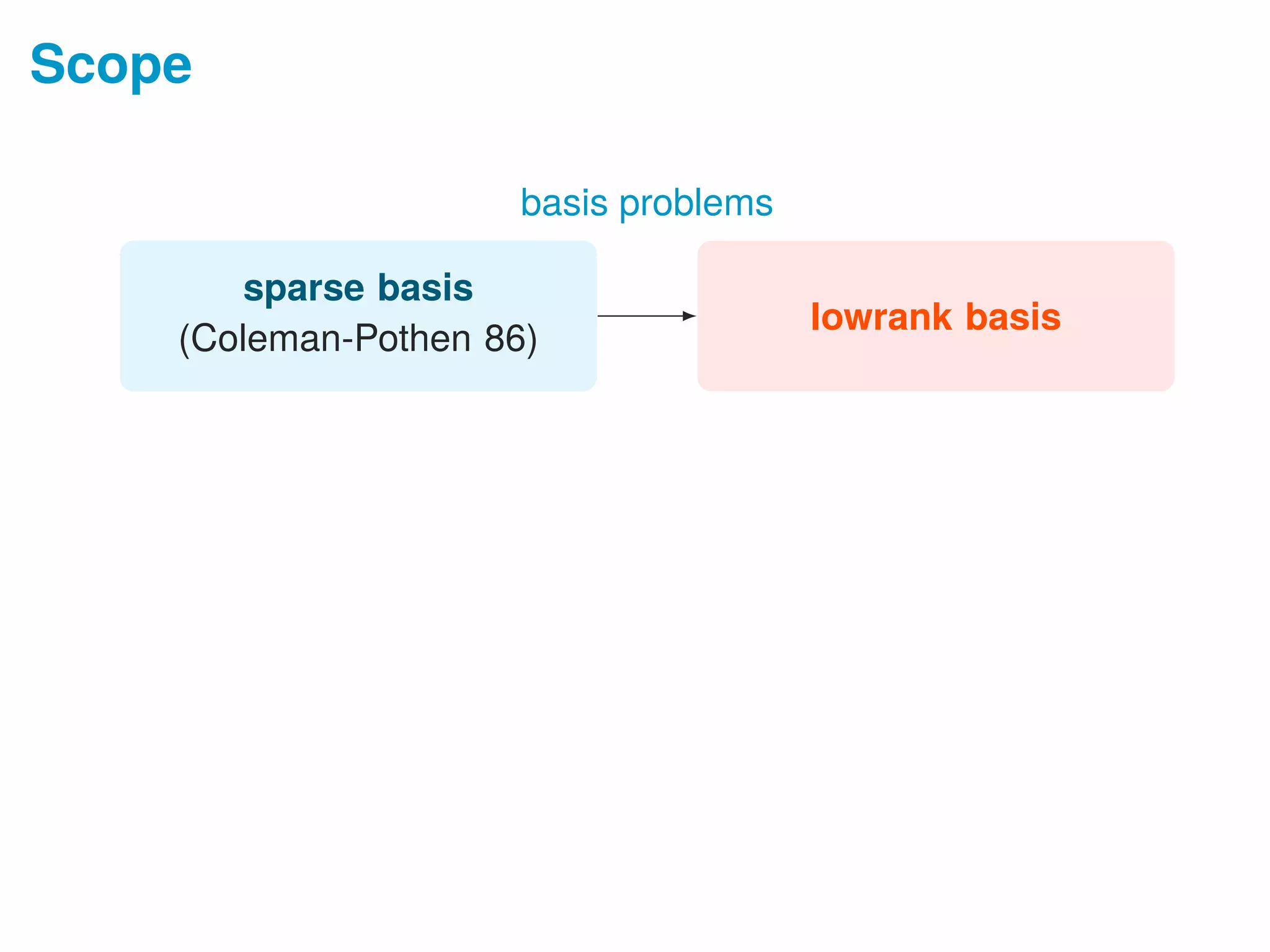
7. Scope
lowrank basis
sparse basis
(Coleman-Pothen 86)
basis problems
lowrank matrix
sparse vector
(Qu-Sun-Wright 14)
single element problems
• sparse vector problem is NP-hard [Coleman-Pothen 1986]
5 / 29

8. Scope
lowrank basis
sparse basis
(Coleman-Pothen 86)
basis problems
lowrank matrix
sparse vector
(Qu-Sun-Wright 14)
single element problems
• sparse vector problem is NP-hard [Coleman-Pothen 1986]
• Related studies: dictionary learning [Sun-Qu-Wright 14], sparse PCA
[Spielman-Wang-Wright],[Demanet-Hand 14]
5 / 29

9. Applications
• memory-efficient representation of matrix subspace
• matrix compression beyond SVD
• dictionary learning
• string theory: rank-deficient matrix in rectangular subspace
• image separation
• accurate eigenvector computation
• maximum-rank completion (discrete mathematics)
• ...
6 / 29

10. 1 The low-rank basis problem
2 Algorithm
3 Convergence Guarantee
4 Experiments
7 / 29

11. Abstract greedy algorithm
Algorithm 1 Greedy meta-alg. for computing a low-rank basis
Input: Subspace M ⊆ Rm×n
of dimension d.
Output: Basis B = {X∗
1
,. . . ,X∗
d
} of M.
Initialize B = ∅.
for = 1,. . . ,d do
Find X∗ ∈ M of lowest possible rank s.t. B ∪ {X∗} is linearly
independent.
B ← B ∪ {X∗}
• If each step is successful, this finds the required basis!
8 / 29

12. Greedy algorithm: lemma
Lemma
X∗
1
,. . . ,X∗
d
: output of greedy algorithm.
For any ∈ {1,. . . ,d} and lin. indep. {X1,. . . ,X } ⊆ M with
rank(X1) ≤ · · · ≤ rank(X ),
rank(Xi ) ≥ rank(X∗
i ) for i = 1,. . . , .
9 / 29

13. Greedy algorithm: lemma
Lemma
X∗
1
,. . . ,X∗
d
: output of greedy algorithm.
For any ∈ {1,. . . ,d} and lin. indep. {X1,. . . ,X } ⊆ M with
rank(X1) ≤ · · · ≤ rank(X ),
rank(Xi ) ≥ rank(X∗
i ) for i = 1,. . . , .
Proof.
If rank(X ) < rank(X∗), then rank(Xi ) < rank(X∗) for i ≤ .
But since one Xi must be linearly independent from X∗
1
,. . . ,X∗
−1
, this
contradicts the choice of X∗.
(Adaption of standard argument from matroid theory.)
9 / 29

14. Greedy algorithm: justification
Theorem
X∗
1
,. . . ,X∗
d
: lin. indep. output of greedy algorithm. Then {X1,. . . ,X } is
of minimal rank iff
rank(Xi ) = rank(X∗
i ) for i = 1,. . . , .
In particular, {X∗
1
,. . . ,X∗} is of minimal rank.
• Analogous result for sparse basis problem in [Coleman, Pothen 1986]
10 / 29

15. The single matrix problem
minimize rank(X)
subject to X ∈ M {0}.
• NP-hard of course (since sparse vector is)
11 / 29

16. The single matrix problem
minimize rank(X)
subject to X ∈ M {0}.
• NP-hard of course (since sparse vector is)
Nuclear norm heuristic ( A ∗ := σi (A))
minimize X ∗
subject to X ∈ M, X F = 1.
NOT a convex relaxation due to non-convex constraint.
11 / 29

17. Algorithm Outline (for the single matrix problem)
Phase I: rank estimate
Y = Sτ(X), X =
PM (Y)
PM (Y) F
until rank(Y) converges
Phase II: alternating projection
Y = Tr (X), X =
PM (Y)
PM (Y) F
estimated r = rank(Y)
12 / 29

18. Algorithm Outline (for the single matrix problem)
Phase I: rank estimate
Y = Sτ(X), X =
PM (Y)
PM (Y) F
until rank(Y) converges
Phase II: alternating projection
Y = Tr (X), X =
PM (Y)
PM (Y) F
estimated r = rank(Y)
12 / 29

19. Shrinkage operator
Shrinkage operator (soft thresholding) for X = UΣVT
:
Sτ(X) = USτ(Σ)VT
, Sτ(Σ) = diag(σ1 − τ,. . . ,σrank(X) − τ)+
Fixed-point iteration
Y = Sτ(X), X =
PM (Y)
PM (Y) F
13 / 29

20. Shrinkage operator
Shrinkage operator (soft thresholding) for X = UΣVT
:
Sτ(X) = USτ(Σ)VT
, Sτ(Σ) = diag(σ1 − τ,. . . ,σrank(X) − τ)+
Fixed-point iteration
Y = Sτ(X), X =
PM (Y)
PM (Y) F
Interpretation: [Cai, Candes, Shen 2010], [Qu, Sun, Wright @NIPS 2014]
block coordinate descent (a.k.a. alternating direction) for
minimize
X,Y
τ Y ∗ +
1
2
Y − X 2
F
subject to X ∈ M, and X F = 1,
[Qu, Sun, Wright @NIPS 2014]: analogous method for sparsest vector.
13 / 29

21. The use as a rank estimator
Y = Sτ(X), X =
PM (Y)
PM (Y) F
• The fixed point of Y would be a matrix of low-rank r, which is close
to, but not in M if r > 1.
• otherwise, it would be a fixed point of
Y =
Sτ (Y)
Sτ (Y) F
which can hold only for rank-one matrices.
• The fixed point of X usually has full rank, and “too large“ σi 1.
⇒ Need further improvement, but accept r as rank estimate.
14 / 29

22. Algorithm Outline (for the single matrix problem)
Phase I: rank estimate
Y = Sτ(X), X =
PM (Y)
PM (Y) F
until rank(Y) converges
Phase II: alternating projection
Y = Tr (X), X =
PM (Y)
PM (Y) F
estimated r = rank(Y)
15 / 29

23. Obtaining solution: truncation operator
Truncation operator (hard thresholding) for X = UΣVT
:
Tr (X) = UTr (Σ)VT
, Tr (Σ) = diag(σ1,. . . ,σr,0,. . . ,0)
Fixed-point iteration
Y = Tr (X), X =
PM (Y)
PM (Y) F
16 / 29

24. Obtaining solution: truncation operator
Truncation operator (hard thresholding) for X = UΣVT
:
Tr (X) = UTr (Σ)VT
, Tr (Σ) = diag(σ1,. . . ,σr,0,. . . ,0)
Fixed-point iteration
Y = Tr (X), X =
PM (Y)
PM (Y) F
Interpretation: alternating projection method for finding
X∗ ∈ {X ∈ M : X F = 1} ∩ {Y : rank(Y) ≤ r} .
16 / 29

25. Greedy algorithm: pseudocode
Algorithm 2 Greedy algorithm for computing a low-rank basis
Input: Basis M1,. . . Md ∈ Rm×n
for M
Output: Low-rank basis X1,. . . ,Xd of M.
for = 1,. . . ,d do
Phase I on X , obtain rank estimate r.
Phase II on X with rank r, obtain X ∈ M of rank r.
• To force linear independence, restarting is sometimes necessary:
X is always initialized and restarted in span{X1,. . . ,X −1}⊥ ∩ M.
• Phase I output X is Phase II input
17 / 29

26. 1 The low-rank basis problem
2 Algorithm
3 Convergence Guarantee
4 Experiments
18 / 29

27. Observed convergence (single initial guess)
m = 20,n = 10,d = 5, exact ranks: (1,2,3,4,5).
• ranks recovered in “wrong” order (2,1,5,3,4)
19 / 29

28. Observed convergence (several initial guesses)
• ranks recovered in correct order
20 / 29

29. Local convergence of Phase II
Rr := {X : rank(X) = r}, B := {X ∈ M : X F = 1}
TX∗ (N ): tangent space of manifold N at X∗
Theorem
Assume X∗ ∈ Tr ∩ B has rank r, input of Phase II, and
TX∗ Rr ∩ TX∗ B = ∅. Then Phase II is locally linearly convergent:
Xnew − X∗ F
X − X∗ F
cos θ
21 / 29

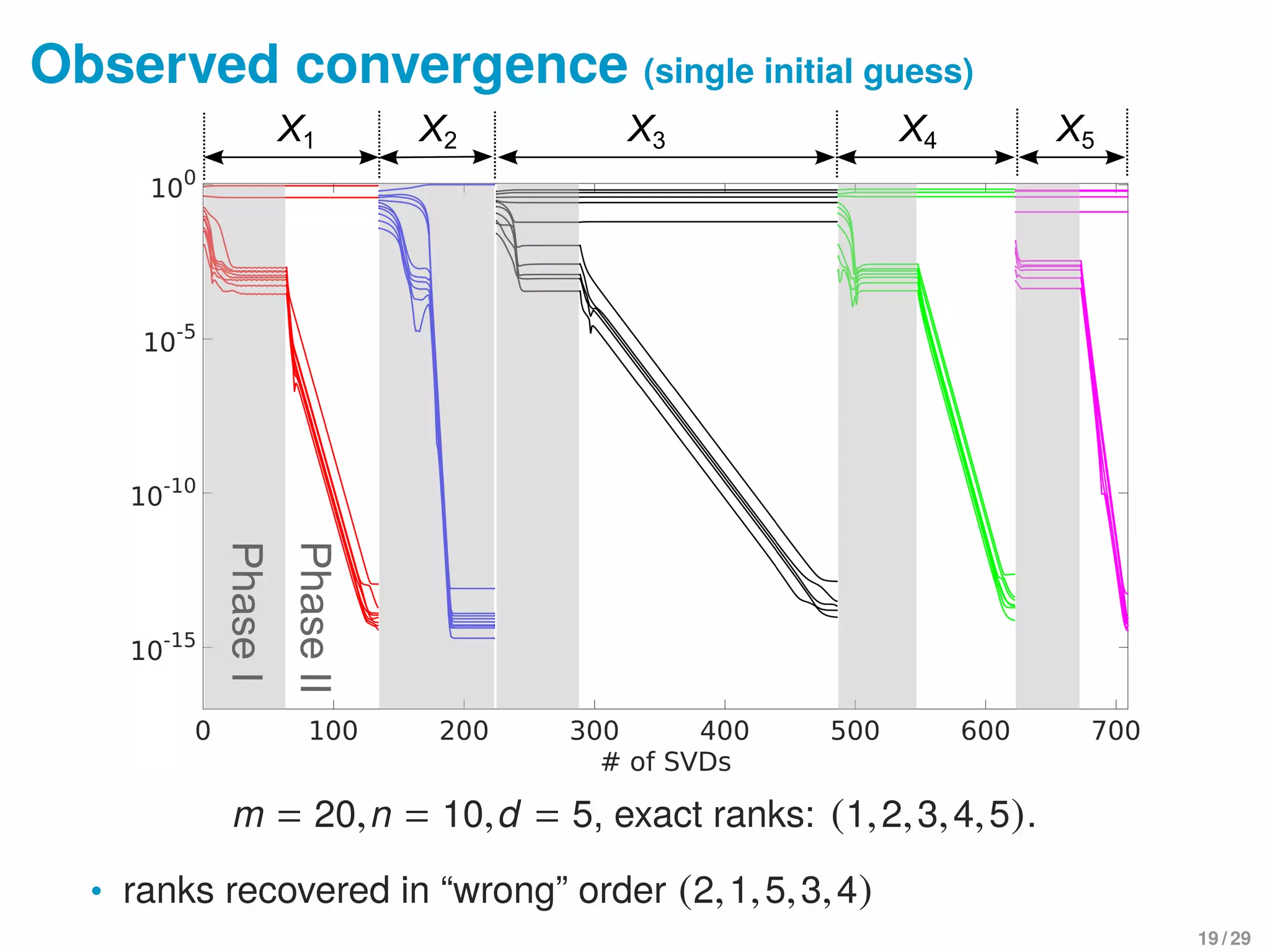
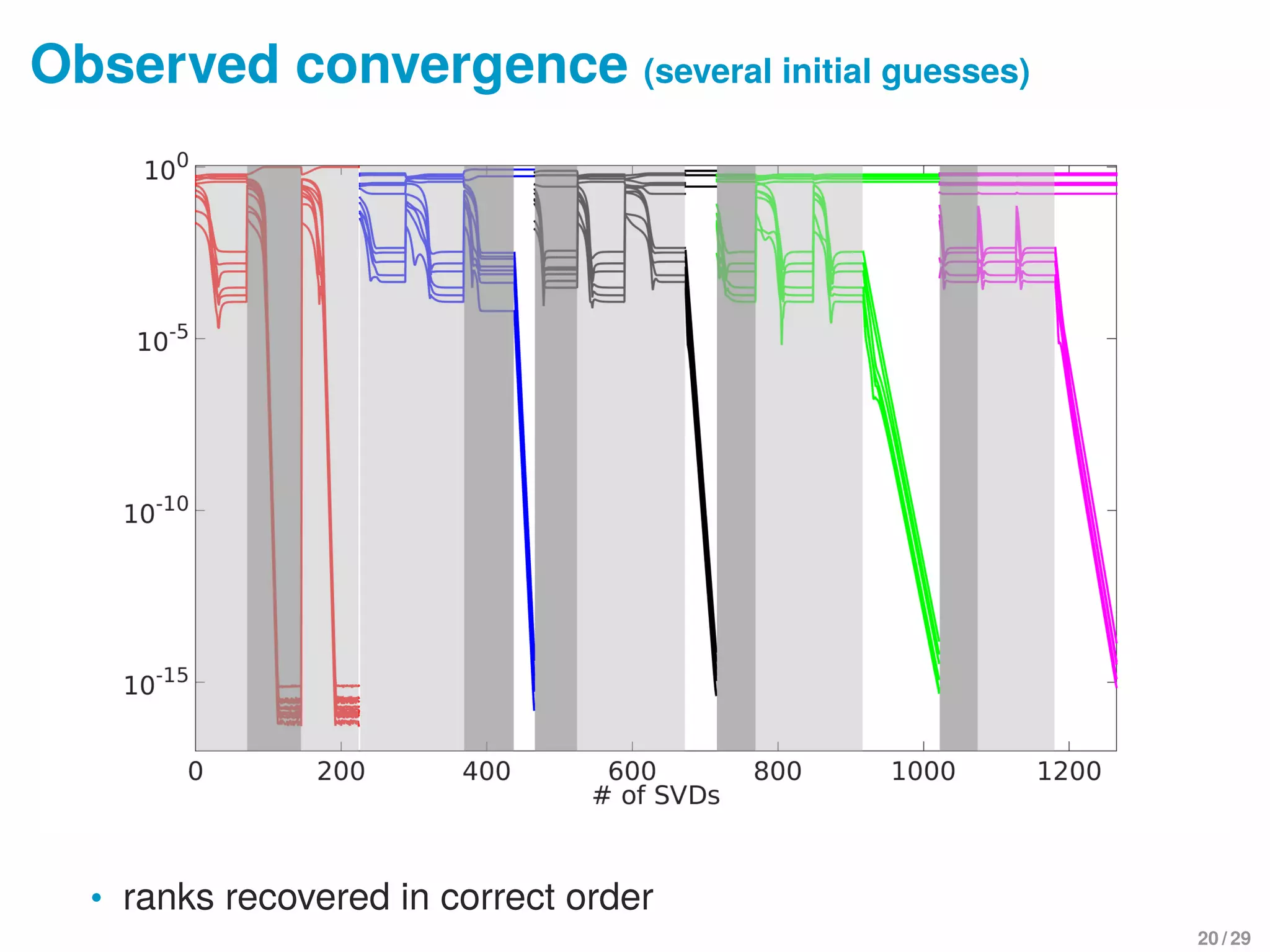
30. Local convergence of Phase II
Rr := {X : rank(X) = r}, B := {X ∈ M : X F = 1}
TX∗ (N ): tangent space of manifold N at X∗
Theorem
Assume X∗ ∈ Tr ∩ B has rank r, input of Phase II, and
TX∗ Rr ∩ TX∗ B = ∅. Then Phase II is locally linearly convergent:
Xnew − X∗ F
X − X∗ F
cos θ
• Follows from a meta-theorem on alternating projections in
nonlinear optimization [Lewis, Luke, Malick 2009]
• We provide “direct” linear algebra proof
• Assumption holds if X∗ is isolated rank-r matrix in M
21 / 29

31. Local convergence: intuition
X∗
TX∗ B
TX∗ Rr
cos θ ≈ 1√
2
X∗
TX∗ B
TX∗ Rr
cos θ ≈ 0.9
Xnew − X∗ F
X − X∗ F
≤ cos θ + O( X − X∗
2
F )
θ ∈ (0, π
2
]: subspace angle between TX∗ B and TX∗ Rr
cos θ = max
X∈TX∗ B
Y∈TX∗ Rr
| X,Y F |
X F Y F
.
22 / 29

32. 1 The low-rank basis problem
2 Algorithm
3 Convergence Guarantee
4 Experiments
23 / 29

33. Results for synthetic data
exact ranks av. sum(ranks) av. Phase I err (iter) av. Phase II err (iter)
( 1 , 1 , 1 , 1 , 1) 5.05 2.59e-14 (55.7) 7.03e-15 (0.4)
( 2 , 2 , 2 , 2 , 2 ) 10.02 4.04e-03 (58.4) 1.04e-14 (9.11)
( 1 , 2 , 3 , 4 , 5) 15.05 6.20e-03 (60.3) 1.38e-14 (15.8)
( 5 , 5 , 5 , 10 , 10) 35.42 1.27e-02 (64.9) 9.37e-14 (50.1)
( 5 , 5 , 10 , 10 , 15) 44.59 2.14e-02 (66.6) 3.96e-05 (107)
Table: m = n = 20, d = 5, random initial guess.
exact ranks av. sum (ranks) av. Phase I err (iter) av. Phase II err (iter)
( 1 , 1 , 1 , 1 , 1) 5.00 6.77e-15 (709) 6.75e-15 (0.4)
( 2 , 2 , 2 , 2 , 2) 10.00 4.04e-03 (393) 9.57e-15 (9.0)
( 1 , 2 , 3 , 4 , 5) 15.00 5.82e-03 (390) 1.37e-14 (18.5)
( 5 , 5 , 5 , 10 , 10) 35.00 1.23e-02 (550) 3.07e-14 (55.8)
( 5 , 5 , 10 , 10 , 15) 44.20 2.06e-02 (829) 8.96e-06 (227)
Table: Five random initial guesses.
24 / 29

34. Image separation
original
mixed
computed
25 / 29

35. Link to tensor decomposition
Rank-one basis: M = span{a1
bT
1
,. . . ,ad
bT
d
}
If M1,. . . ,Md is any basis, then
Mk =
d
=1
ck, a bT
(k = 1,. . . ,d) ⇐⇒ T =
d
=1
a ◦ b ◦ c ,
where T is the third-order tensor with slices M . ⇒ rank(T ) = d.
Suggests finding rank-one basis using CP decomposition algorithms
(ALS, Generalized Eigenvalue, ...)
but CP not enough for higher-rank case
26 / 29

36. Comparison with CP for rank-1 basis
matrix size n
100 200 300 400 500 600 700 800 900 1000
10-3
10-2
10-1
100
101
102
103
Runtime(s)
Phase I
Phase II
Tensorlab
matrix size n
100 200 300 400 500 600 700 800 900 1000
10-15
10-10
10-5
100
Error
Phase I
Phase II
Tensorlab
d = 10, varying m = n between 50 and 500.
27 / 29

37. Comparison with CP for rank-1 basis
dimension d
2 4 6 8 10 12 14 16 18 20
10-4
10-3
10-2
10-1
100
Runtime(s)
Phase I
Phase II
Tensorlab
dimension d
2 4 6 8 10 12 14 16 18 20
10-15
10-10
10-5
100
Error
Phase I
Phase II
Tensorlab
m = n = 10, varying d between 2 and 20.
28 / 29

38. Summary and outlook
Summary
• low-rank basis problem
• lots of applications
• NP-hard
• introduced practical greedy algorithm
Future work
• further probabilistic analysis of Phase I
• finding low-rank tensor basis
29 / 29

39. Application: matrix compression
• classical SVD compression: achieves ≈
r
n
compression
A ≈ U Σ VT
30 / 29

40. Application: matrix compression
• classical SVD compression: achieves ≈
r
n
compression
A ≈ U Σ VT
further, suppose m = st and reshape ith column of U:
ui,1
ui,2
.
.
.
ui,s
.
.
.
ui,st
→
ui,1 ui,s+1 · · · ui,s(t−1)+1
.
.
.
.
.
.
. . .
.
.
.
ui,s ui,2s · · · ui,st
≈ Uu,i Σu,i VT
u,i
• Compression: ≈
r1r2
n2
, “squared” reduction
30 / 29

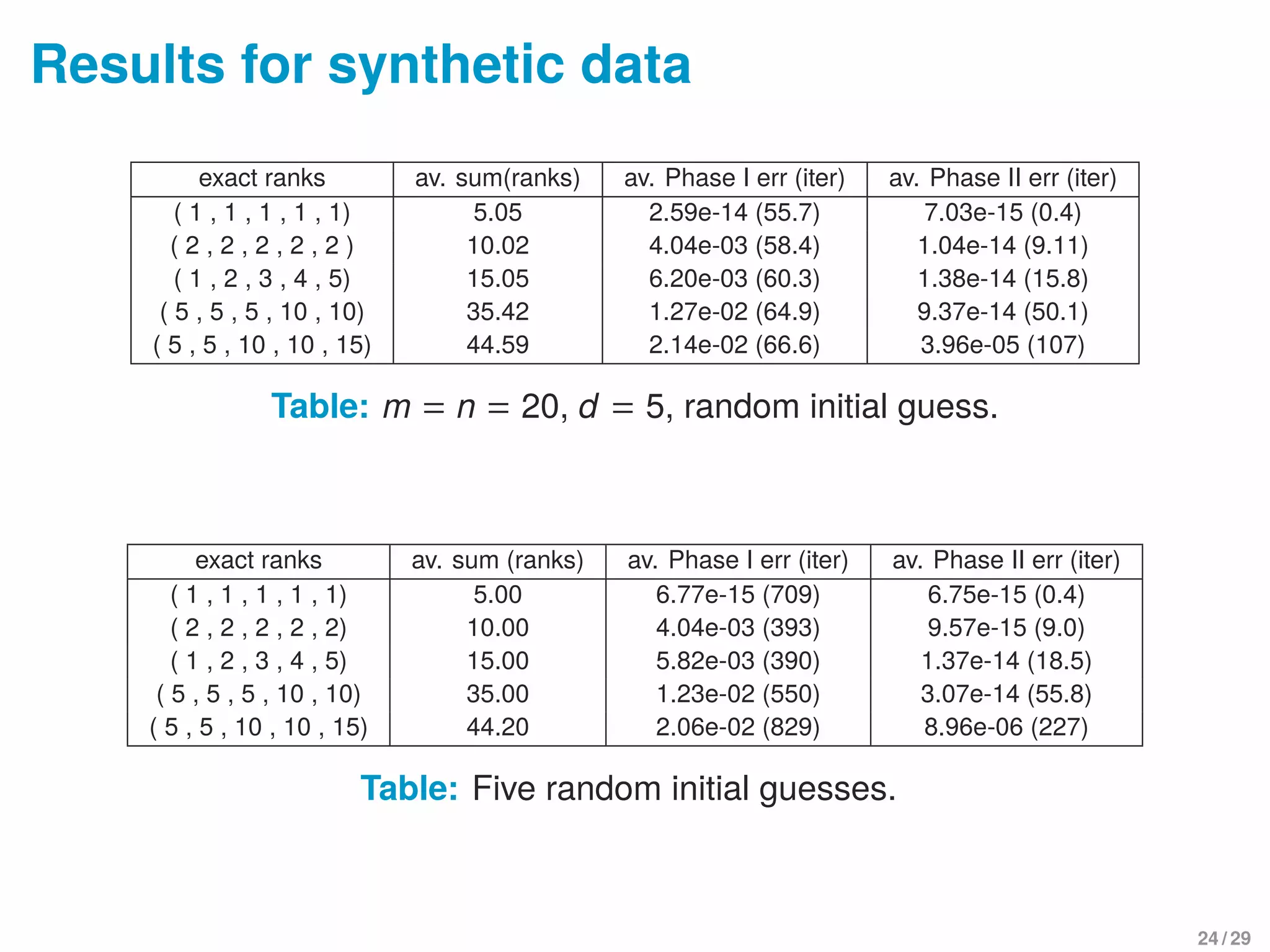
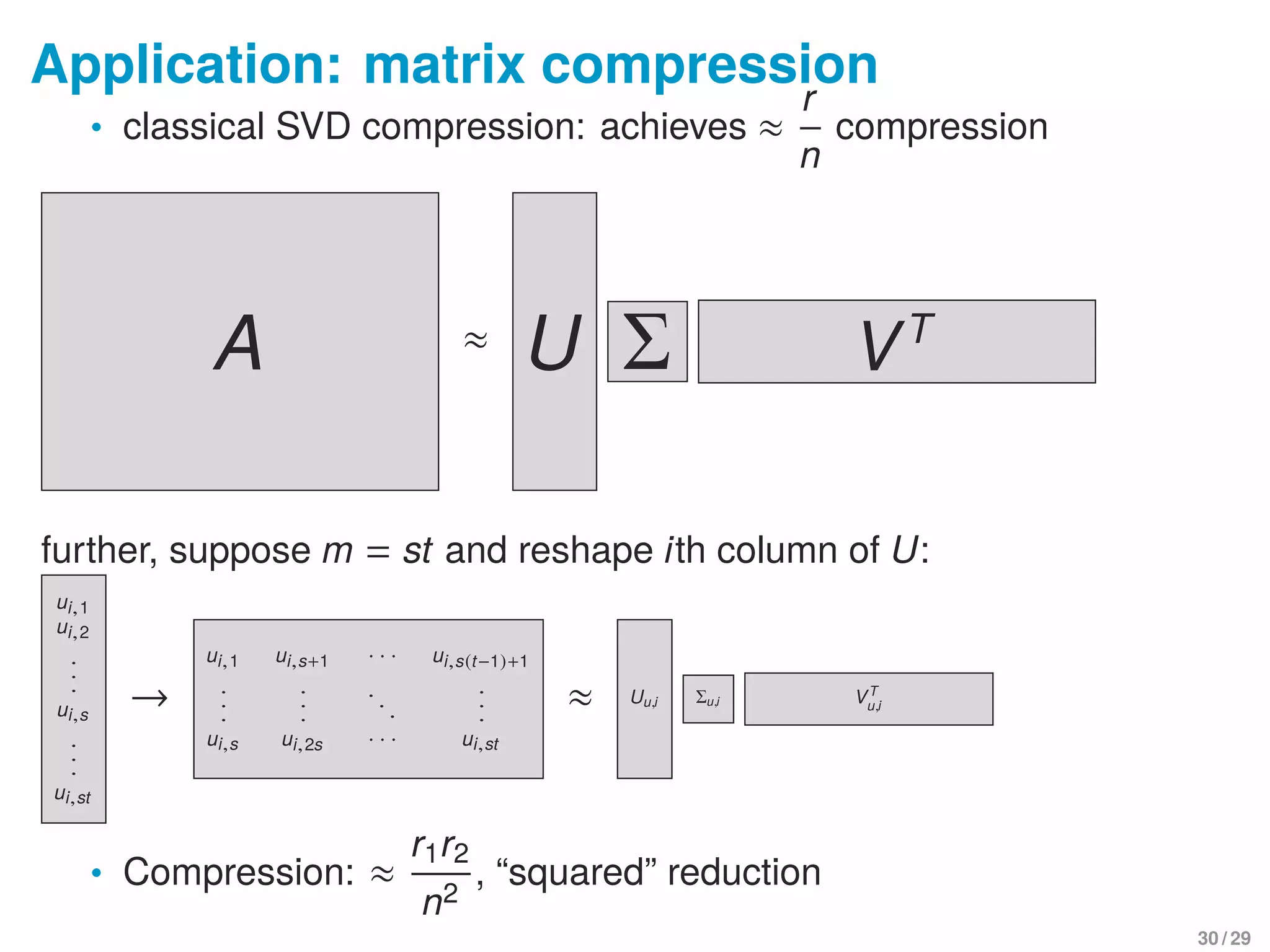
41. Finding right “basis” for storage reduction
U = [U1,. . . ,Ur], ideally, each column Ui = [ui,1,ui,2,. . . ,ui,st]T
has
low-rank structure when matricized
ui,1
ui,2
.
.
.
ui,s
.
.
.
ui,st
→
ui,1 ui,s+1 · · · ui,s(t−1)+1
.
.
.
.
.
.
. . .
.
.
.
ui,s ui,2s · · · ui,st
≈ Uu,i VT
u,i for i = 1,. . . ,r
• More realistically: ∃ Q ∈ Rr×r
s.t. UQ has such property
⇒ finding low-rank basis for matrix subspace spanned by
mat(U1),mat(U2),. . . ,mat(Ur )
31 / 29

42. Compressible matrices
• FFT matrix e2π ij
n : each mat(column) is rank-1
• Any circulant matrix eigenspace
• Graph Laplacian eigenvectors:
• rank 2: ladder, circular
• rank 3: binary tree, cycle, path, wheel
• rank 4: lollipop
• rank 5: barbell
• ...
⇒ explanation is open problem, fast FFT-like algorithms?
32 / 29

43. Eigenvectors of multiple eigenvalues
A[x1,x2,. . . ,xk] = λ[x1,x2,. . . ,xk]
• eigenvector x for Ax = λx is not determined uniquely +
non-differentiable
• numerical practice: content with computing span(x1,x2)
extreme example: I, any vector is eigenvector!
• but perhaps




1
,

1

, . . .
1




is a “good” set of eigenvectors
• why? low-rank, low-memory!
33 / 29

44. Computing eigenvectors of multiple
eigenvalues
F : FFT matrix
A =
1
n
Fdiag(1 + ,1 + ,1 + ,1 + ,1 + ,6,. . . ,n2
)F∗
, = O(10−10
)
• cluster of five eigenvalues ≈ 1
• “exact”, low-rank eigenvectors: first five columns of F.
v1 v2 v3 v4 v5 memory
eig 4.2e-01 1.2e+00 1.4e+00 1.4e+00 1.5e+00 O(n2
)
eig+Alg. 2 1.2e-12 1.2e-12 1.2e-12 1.2e-12 2.7e-14 O(n)
Table: Eigenvector accuracy, before and after finding low-rank basis.
• MATLAB’s eig fails to find accurate eigenvectors.
• accurate eigenvectors obtained by finding low-rank basis.
34 / 29

45. Restart
Algorithm 3 Restart for linear independence
Input: Orthogonal projection Q −1 onto M ∩ Span(X∗
1
,. . . ,X∗
−1
)⊥, cur-
rent matrix X and tolerance restarttol > 0.
Output: Eventually replaced X .
if Q −1(X ) F < restarttol (e.g. 0.01) then
Replace X by a random element in Range(Q −1). X ← X / X F
• Linear dependence monitored by projected norm Q −1(X ) F
35 / 29

46. Linear algebra convergence proof
TX∗ Rr = [U∗ U⊥
∗ ]
A B
C 0
[V∗ V⊥
∗ ]T
. (1)
X − X∗ = E + O( X − X∗
2
F )
with E ∈ TX∗ B. Write E = [U∗ U⊥
∗ ][ A B
C D ][V∗ V⊥
∗ ]T
. By (1)
D 2
F
≥ sin2
θ · E 2
F
. ∃F,G orthogonal s.t.
X = FT Σ∗ + A 0
0 D
GT
+ O( E 2
F ).
Tr (X) − X∗ F =
A + Σ∗ 0
0 0
−
Σ∗ −B
−C CΣ−1
∗ B F
+ O( E 2
F )
=
A B
C 0 F
+ O( E 2
F ).
So
Tr (X) − X∗ F
X − X∗ F
=
E 2
F
− D 2
F
+ O( X − X∗
2
F
)
E F + O( X − X∗
2
F
)
≤ 1 − sin2
θ + O( X − X∗
2
F ) = cos θ + O( X − X∗
2
F )
36 / 29

47. Partial result for Phase I
Corollary
If r = 1, then already Phase I is locally linearly convergent.
Proof.
In a neighborood of a rank-one matrix, shrinkage and truncation are the
same up to normalization.
• In general, Phase I “sieves out” the non-dominant components to
reveal the rank
37 / 29

48. String theory problem
Given A1,. . . ,Ak ∈ Rm×n
, find ci ∈ R s.t.
rank(c1A1 + c2A2 + · · · + ckAk ) < n
A1 A2 . . . Ak Q = 0, Q = [q1,. . . ,qnk−m]
• finding null vector that is rank-one when matricized
• ⇒ Lowest-rank problem from mat(q1),. . . ,mat(qnk−m) ∈ Rn×k
when rank= 1
• slow (or non-)convergence in practice
• NP-hard? probably.. but unsure (since special case)
38 / 29