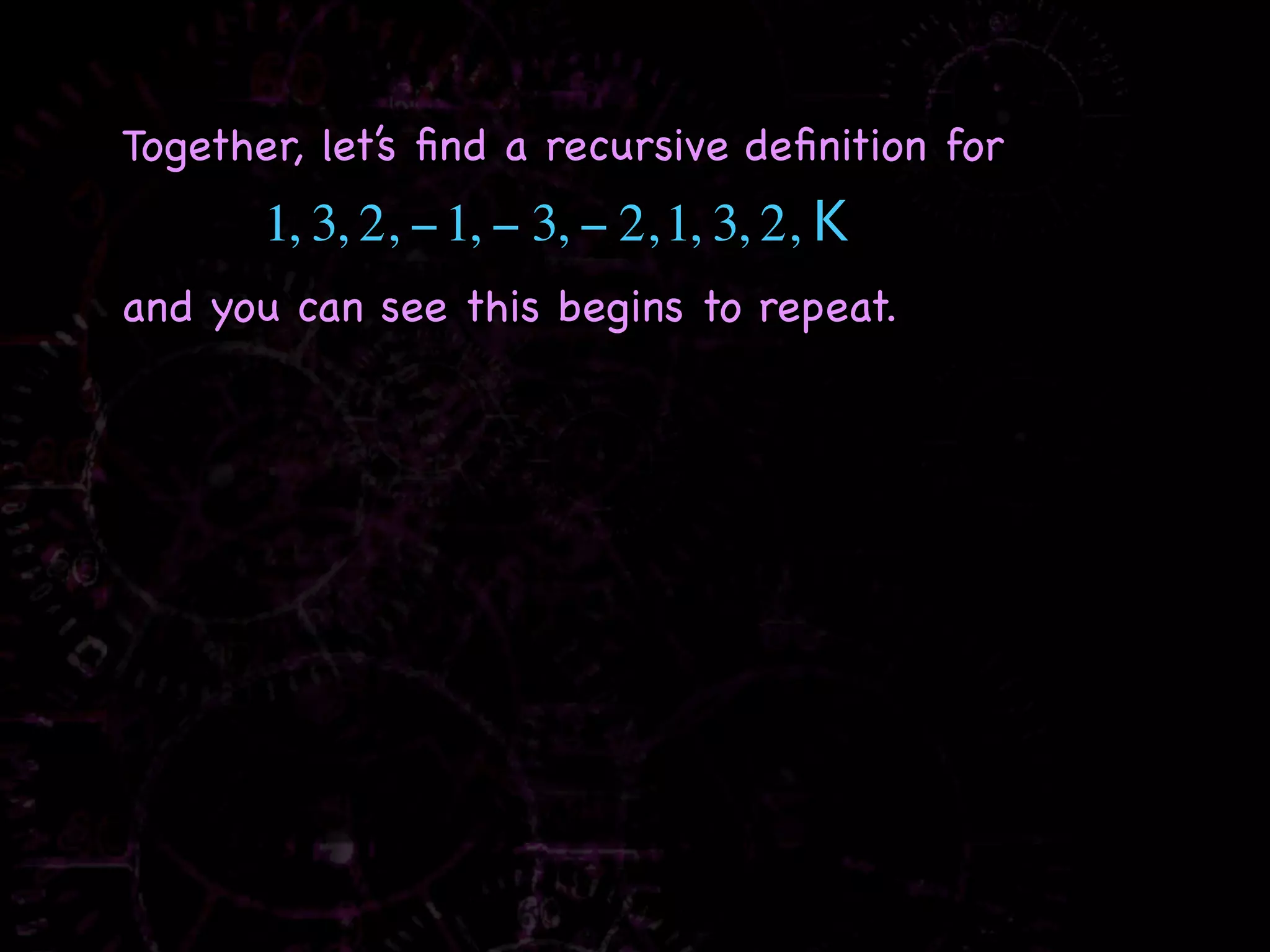
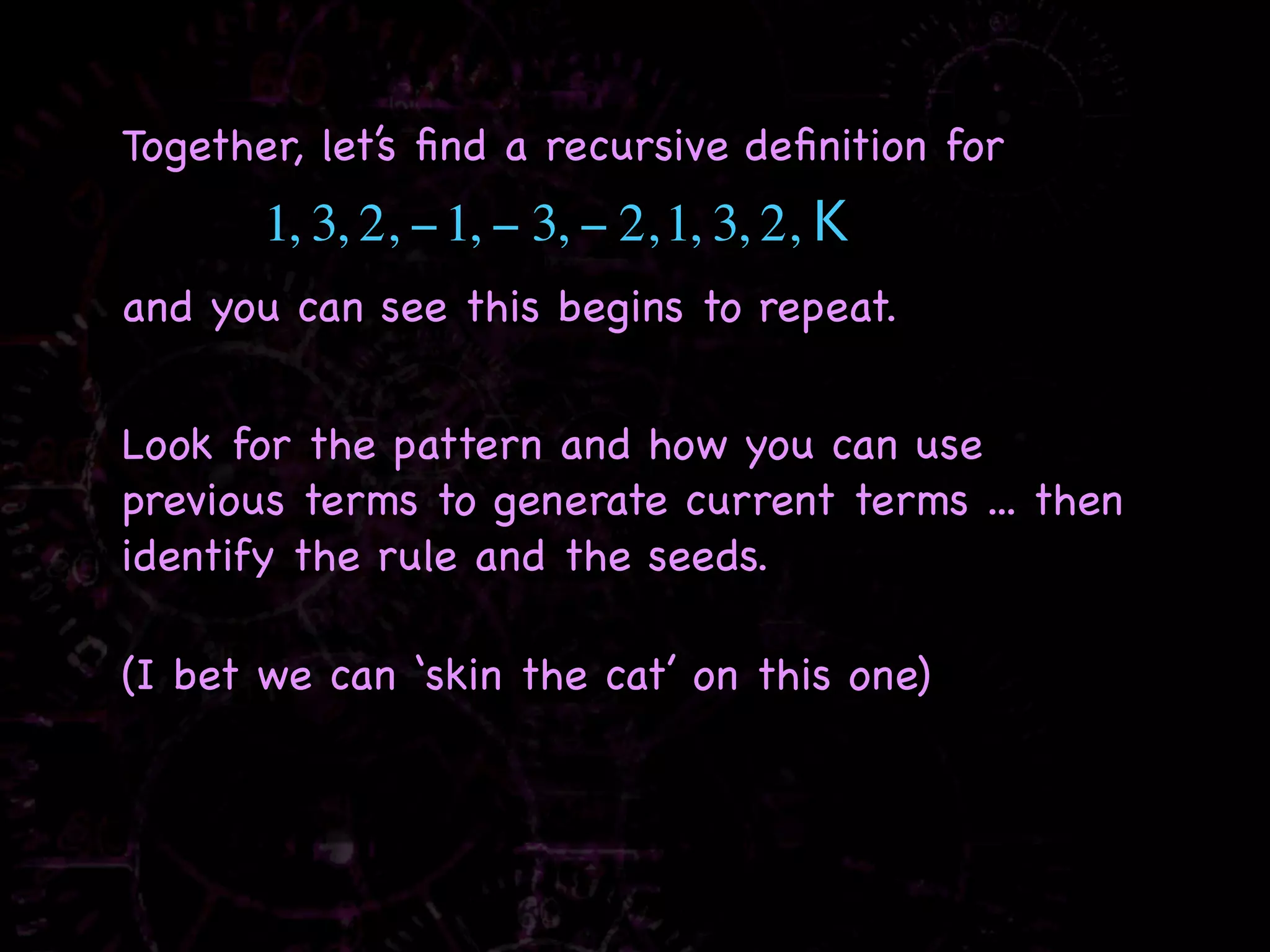
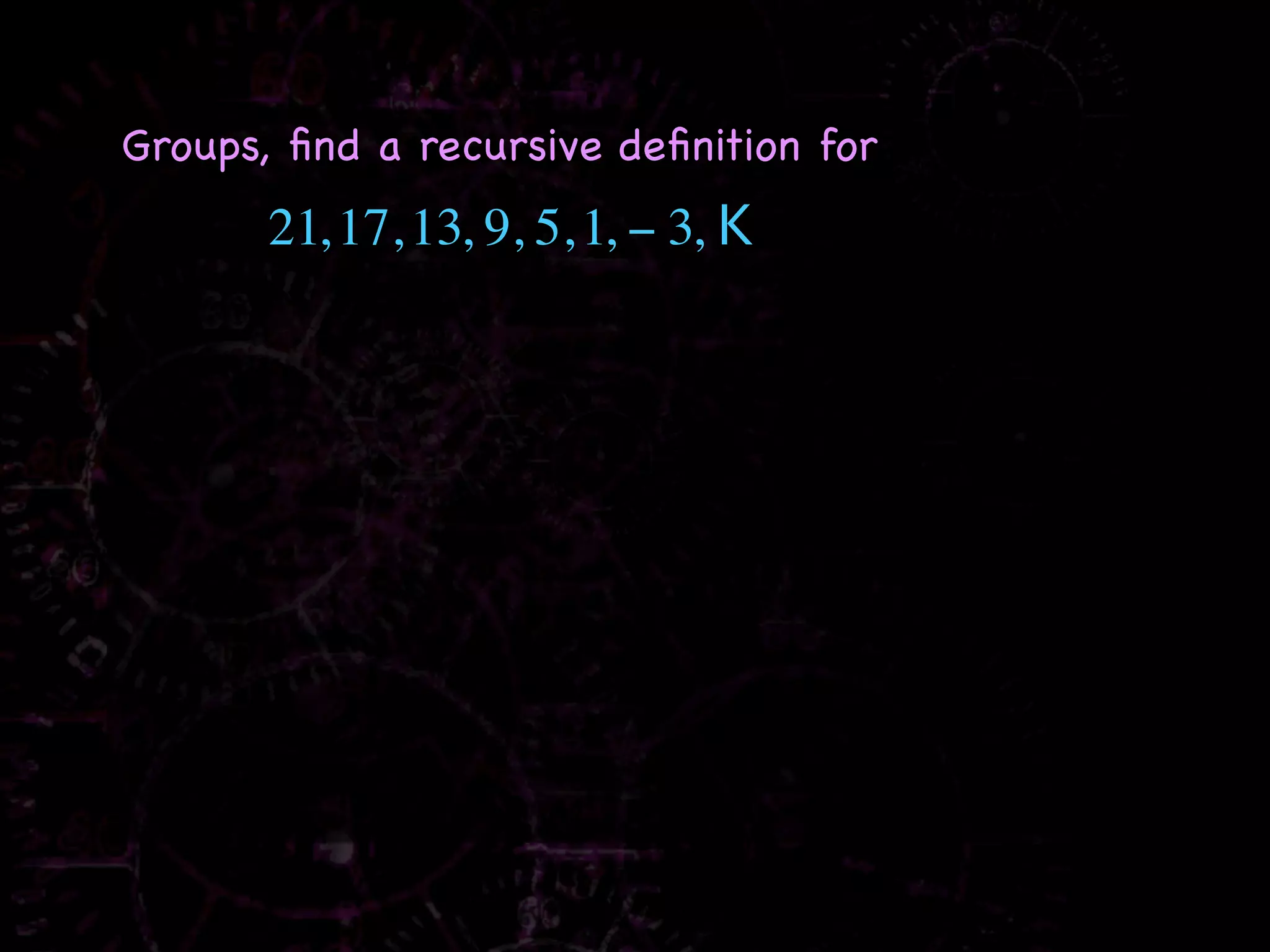
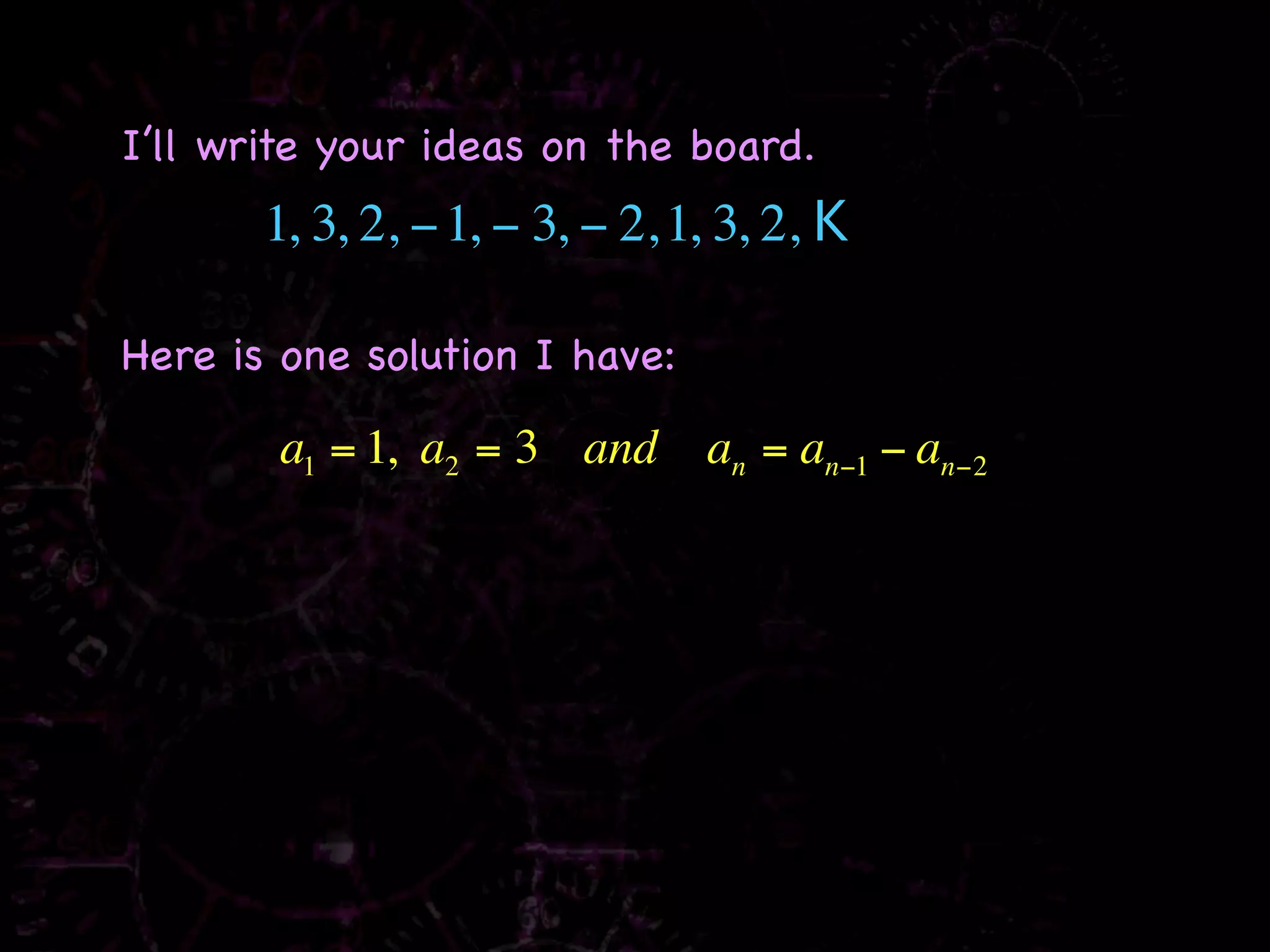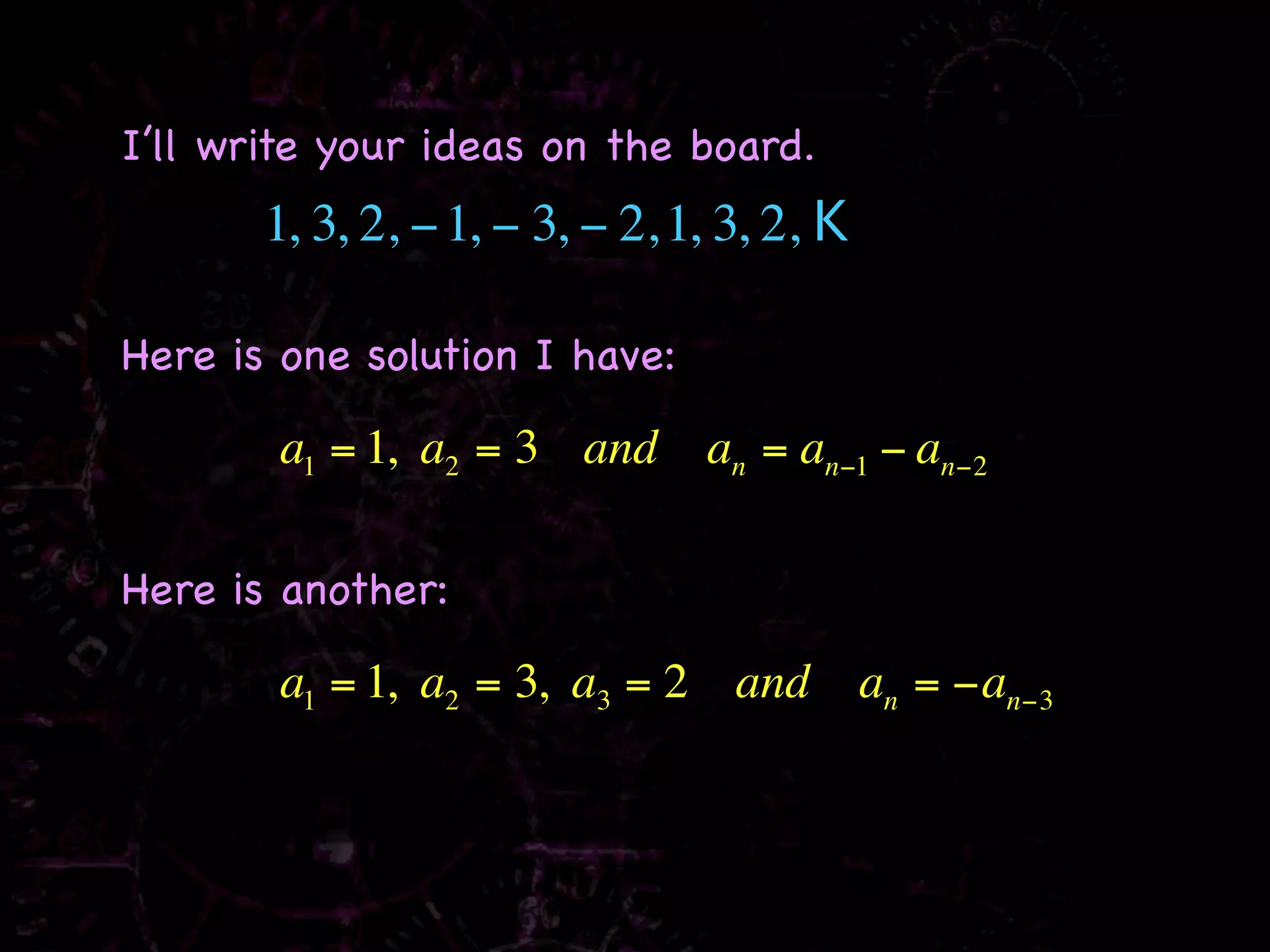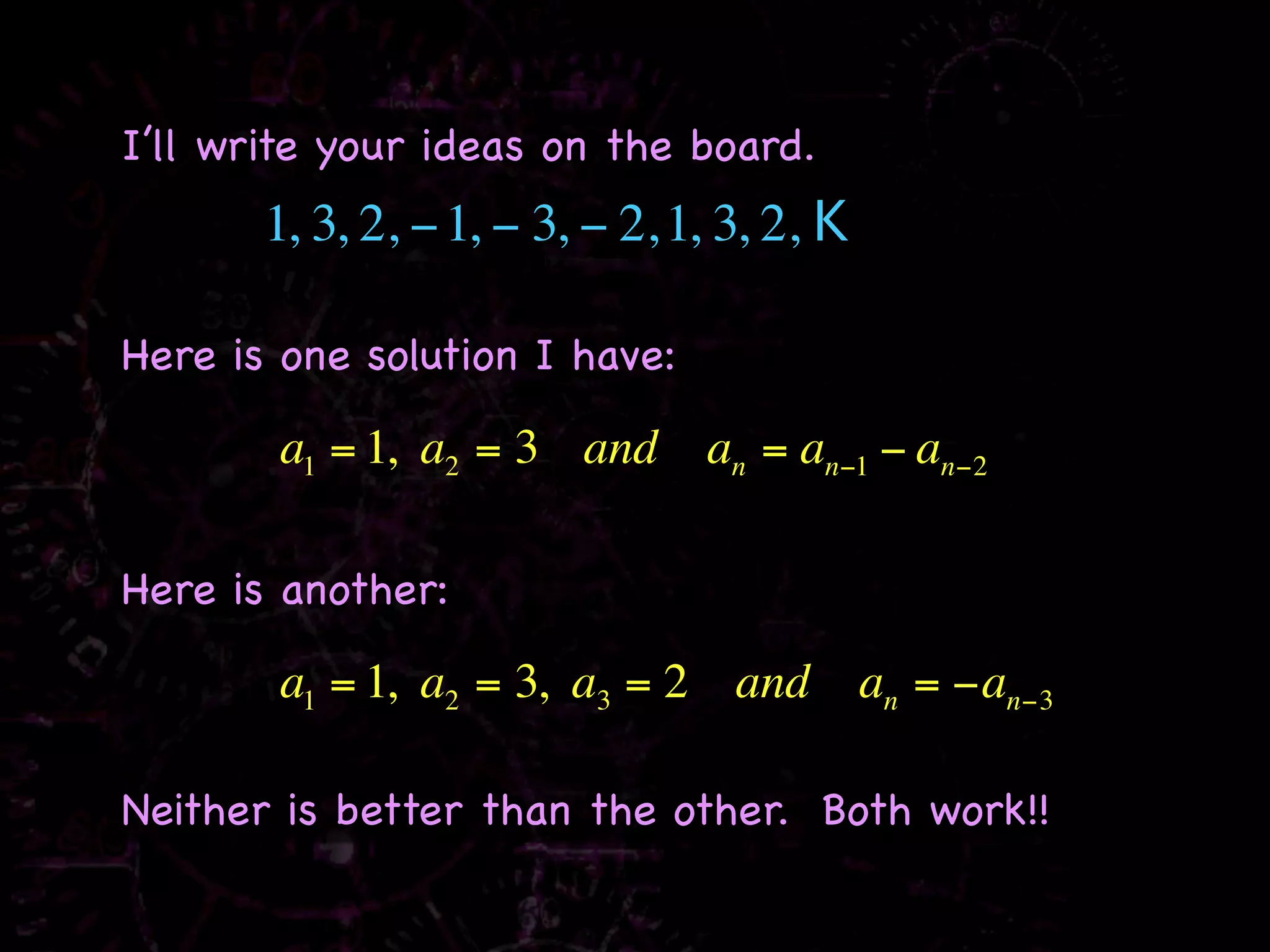The document discusses recursive rules for defining sequences. It explains that a recursive rule defines subsequent terms of a sequence using previous terms, with one or more initial terms provided. Examples are worked through, such as finding the first five terms of the sequence where a1 = 3 and an = 2an-1 - 1, which are 3, 5, 9, 17, 33. Other sequences discussed include the Fibonacci sequence and examples of finding recursive rules to define other given sequences.

1. 11.1 Sequences & Summation Notation
Day Two
John 14:15 "If you love me, you will keep my commandments."

2. Not all sequences can be defined with an explicit
rule.

3. Not all sequences can be defined with an explicit
rule.
A Recursive rule is one where one or more initial
terms are given and all subsequent terms are
defined using previous terms.

4. Not all sequences can be defined with an explicit
rule.
A Recursive rule is one where one or more initial
terms are given and all subsequent terms are
defined using previous terms.
an

5. Not all sequences can be defined with an explicit
rule.
A Recursive rule is one where one or more initial
terms are given and all subsequent terms are
defined using previous terms.
an
next term

6. Not all sequences can be defined with an explicit
rule.
A Recursive rule is one where one or more initial
terms are given and all subsequent terms are
defined using previous terms.
an an+1
next term

7. Not all sequences can be defined with an explicit
rule.
A Recursive rule is one where one or more initial
terms are given and all subsequent terms are
defined using previous terms.
an an+1
previous next term
term

8. Not all sequences can be defined with an explicit
rule.
A Recursive rule is one where one or more initial
terms are given and all subsequent terms are
defined using previous terms.
an−1 an an+1
previous next term
term

9. Not all sequences can be defined with an explicit
rule.
A Recursive rule is one where one or more initial
terms are given and all subsequent terms are
defined using previous terms.
an−1 an an+1
second previous next term
previous term
term

10. Not all sequences can be defined with an explicit
rule.
A Recursive rule is one where one or more initial
terms are given and all subsequent terms are
defined using previous terms.
an−2 an−1 an an+1
second previous next term
previous term
term

11. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1

12. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1
seed

13. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1
seed current = 2(previous)-1

14. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1
seed current = 2(previous)-1
a1 = 3

15. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1
seed current = 2(previous)-1
a1 = 3
a2 = 2 ( 3) − 1 = 5

16. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1
seed current = 2(previous)-1
a1 = 3
a2 = 2 ( 3) − 1 = 5
a3 = 2 ( 5 ) − 1 = 9

17. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1
seed current = 2(previous)-1
a1 = 3
a2 = 2 ( 3) − 1 = 5
a3 = 2 ( 5 ) − 1 = 9
a4 = 2 ( 9 ) − 1 = 17

18. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1
seed current = 2(previous)-1
a1 = 3
a2 = 2 ( 3) − 1 = 5
a3 = 2 ( 5 ) − 1 = 9
a4 = 2 ( 9 ) − 1 = 17
a5 = 2 (17 ) − 1 = 33

19. Find the first five terms of the sequence if:
a1 = 3 and an = 2an−1 − 1
seed current = 2(previous)-1
a1 = 3
a2 = 2 ( 3) − 1 = 5
a3 = 2 ( 5 ) − 1 = 9
∴ 3, 5, 9, 17, 33
a4 = 2 ( 9 ) − 1 = 17
a5 = 2 (17 ) − 1 = 33

20. The Fibonacci Sequence
1, 1, 2, 3, 5, 8, 13, 21, K
is defined recursively this way:

21. The Fibonacci Sequence
1, 1, 2, 3, 5, 8, 13, 21, K
is defined recursively this way:
a1 = 1
a2 = 1
an = an−1 + an−2

22. The Fibonacci Sequence
1, 1, 2, 3, 5, 8, 13, 21, K
is defined recursively this way:
a1 = 1 needs 2 seed values
a2 = 1
an = an−1 + an−2

23. The Fibonacci Sequence
1, 1, 2, 3, 5, 8, 13, 21, K
is defined recursively this way:
a1 = 1 needs 2 seed values
a2 = 1
an = an−1 + an−2
Changing the seeds changes the numbers in the
sequence, but it is still a Fibonacci Sequence.

24. Groups: list the first five terms of this sequence:
a1 = 4 and an = 2 ( an−1 + 5 )

25. Groups: list the first five terms of this sequence:
a1 = 4 and an = 2 ( an−1 + 5 )
a1 = 4
a2 = 2 ( 4 + 5 ) = 18
a3 = 2 (18 + 5 ) = 46 ∴ 4, 18, 46, 102, 214
a4 = 2 ( 46 + 5 ) = 102
a5 = 2 (102 + 5 ) = 214

26. Together, let’s find a recursive definition for
1, 3, 2, − 1, − 3, − 2, 1, 3, 2, K
and you can see this begins to repeat.

27. Together, let’s find a recursive definition for
1, 3, 2, − 1, − 3, − 2, 1, 3, 2, K
and you can see this begins to repeat.
Look for the pattern and how you can use
previous terms to generate current terms ... then
identify the rule and the seeds.
(I bet we can ‘skin the cat’ on this one)

28. I’ll write your ideas on the board.
1, 3, 2, − 1, − 3, − 2, 1, 3, 2, K

29. I’ll write your ideas on the board.
1, 3, 2, − 1, − 3, − 2, 1, 3, 2, K
Here is one solution I have:
a1 = 1, a2 = 3 and an = an−1 − an−2

30. I’ll write your ideas on the board.
1, 3, 2, − 1, − 3, − 2, 1, 3, 2, K
Here is one solution I have:
a1 = 1, a2 = 3 and an = an−1 − an−2
Here is another:
a1 = 1, a2 = 3, a3 = 2 and an = −an−3

31. I’ll write your ideas on the board.
1, 3, 2, − 1, − 3, − 2, 1, 3, 2, K
Here is one solution I have:
a1 = 1, a2 = 3 and an = an−1 − an−2
Here is another:
a1 = 1, a2 = 3, a3 = 2 and an = −an−3
Neither is better than the other. Both work!!

32. Groups, find a recursive definition for
21, 17, 13, 9, 5, 1, − 3, K

33. Groups, find a recursive definition for
21, 17, 13, 9, 5, 1, − 3, K
Here is a correct definition:
a1 = 21, and an = an−1 − 4

34. HW #2
“Never tell people how to do things. Tell them what to
do and they will surprise you with their ingenuity.”
George Patton