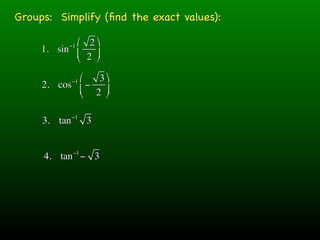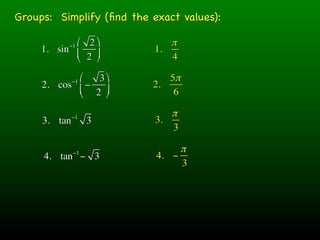The document discusses inverse trigonometric functions and working through examples of evaluating inverse trig expressions. It begins with simplifying inverse trig expressions to find their exact values. Students then work through examples together, showing the step-by-step work to solve inverse trig functions involving multiple nested inverse trig functions. Examples involve finding angles, determining quadrant ranges, and addressing issues like multiple wraparounds. The document emphasizes conceptual understanding over rote calculation.

1. 7.4 Inverse Trig Functions
Day 2
Psalm 46:1
God is our refuge and strength, an ever-present help in trouble.

2. Groups: Simplify (find the exact values):
⎛ 2 ⎞
−1
1. sin ⎜
⎝ 2 ⎟
⎠
⎛
−1 3 ⎞
2. cos ⎜ −
⎝ 2 ⎟
⎠
3. tan −1 3
−1
4. tan − 3

3. Groups: Simplify (find the exact values):
⎛ 2 ⎞
−1 π
1. sin ⎜ 1.
⎝ 2 ⎟
⎠ 4
⎛−1 3 ⎞ 5π
2. cos ⎜ − 2.
⎝ 2 ⎟
⎠ 6
−1 π
3. tan 3 3.
3
−1 π
4. tan − 3 4. −
3

4. Groups: Simplify (find the exact values):
⎛ 2 ⎞
−1 π
1. sin ⎜ 1.
⎝ 2 ⎟
⎠ 4
⎛−1 3 ⎞ 5π
2. cos ⎜ − 2.
⎝ 2 ⎟
⎠ 6
−1 π
3. tan 3 3.
3
−1 π
4. tan − 3 4. −
3
5π
to answer #4 as would be wrong because
3
⎡ π π ⎤
tan x has a range of
−1
⎢ − 2 , 2 ⎥
⎣ ⎦

5. Let’s go through this one together:
⎛ −1 ⎛ 1 ⎞ ⎞
5. tan ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 5 ⎠ ⎠

6. Let’s go through this one together:
⎛ −1 ⎛ 1 ⎞ ⎞
5. tan ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 5 ⎠ ⎠
sin −1 x is + in QI

7. Let’s go through this one together:
⎛ −1 ⎛ 1 ⎞ ⎞
5. tan ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 5 ⎠ ⎠
sin −1 x is + in QI
5
1
θ
a

8. Let’s go through this one together:
⎛ −1 ⎛ 1 ⎞ ⎞
5. tan ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 5 ⎠ ⎠
sin −1 x is + in QI
2 2 2
a +1 = 5
5 2
1 a = 24
θ
a=2 6
a

9. Let’s go through this one together:
⎛ −1 ⎛ 1 ⎞ ⎞
5. tan ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 5 ⎠ ⎠
sin −1 x is + in QI
2 2 2
a +1 = 5
5 2
1 a = 24
θ
a=2 6
a
1
tan θ =
2 6

10. Let’s go through this one together:
⎛ −1 ⎛ 1 ⎞ ⎞
5. tan ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 5 ⎠ ⎠
sin −1 x is + in QI
2 2 2
a +1 = 5
5 2
1 a = 24
θ
a=2 6
a
1
tan θ =
2 6
1 6
= g
2 6 6

11. Let’s go through this one together:
⎛ −1 ⎛ 1 ⎞ ⎞
5. tan ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 5 ⎠ ⎠
sin −1 x is + in QI
2 2 2
a +1 = 5
5 2
1 a = 24
θ
a=2 6
a
1
tan θ =
2 6
1 6
= g
2 6 6
6
=
12

12. ⎛ −1 ⎛ 3 ⎞ ⎞
Groups: 6. cos ⎜ tan ⎜ ⎟ ⎟
⎝ ⎝ 8 ⎠ ⎠

13. ⎛ −1 ⎛ 3 ⎞ ⎞
Groups: 6. cos ⎜ tan ⎜ ⎟ ⎟
⎝ ⎝ 8 ⎠ ⎠
c 2 2
3 +8 =c 2
3
θ c = 73
8

14. ⎛ −1 ⎛ 3 ⎞ ⎞
Groups: 6. cos ⎜ tan ⎜ ⎟ ⎟
⎝ ⎝ 8 ⎠ ⎠
c 2 2
3 +8 =c 2
3
θ c = 73
8
8
cosθ =
73
8 73
=
73

15. ⎛ ⎛ 87π ⎞ ⎞
Together: −1
7. sin ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 4 ⎠ ⎠

16. ⎛ ⎛ 87π ⎞ ⎞
Together: −1
7. sin ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 4 ⎠ ⎠
87π 7π
1st wrap equivalent of is
4 4

17. ⎛ ⎛ 87π ⎞ ⎞
Together: −1
7. sin ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 4 ⎠ ⎠
87π 7π
1st wrap equivalent of is
4 4
⎛ 7π ⎞
−1
∴ = sin ⎜ sin ⎟
⎝ 4 ⎠

18. ⎛ ⎛ 87π ⎞ ⎞
Together: −1
7. sin ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 4 ⎠ ⎠
87π 7π
1st wrap equivalent of is
4 4
⎛ 7π ⎞
−1
∴ = sin ⎜ sin ⎟
⎝ 4 ⎠
−1 ⎡ π π ⎤
since sin is defined from ⎢ − 2 , 2 ⎥
⎣ ⎦

19. ⎛ ⎛ 87π ⎞ ⎞
Together: −1
7. sin ⎜ sin ⎜ ⎟ ⎟
⎝ ⎝ 4 ⎠ ⎠
87π 7π
1st wrap equivalent of is
4 4
⎛ 7π ⎞
−1
∴ = sin ⎜ sin ⎟
⎝ 4 ⎠
−1 ⎡ π π ⎤
since sin is defined from ⎢ − 2 , 2 ⎥
⎣ ⎦
7π π
is incorrect ... but − is correct!
4 4

20. Together: Find approximate first wrap angles.

21. Together: Find approximate first wrap angles.
⎛ 6 ⎞
−1
8. sin ⎜ ⎟ (in radians)
⎝ 7 ⎠

22. Together: Find approximate first wrap angles.
⎛ 6 ⎞
−1
8. sin ⎜ ⎟ (in radians)
⎝ 7 ⎠
1.0297

23. Together: Find approximate first wrap angles.
⎛ 6 ⎞
−1
8. sin ⎜ ⎟ (in radians)
⎝ 7 ⎠
1.0297
9. tan −1 ( −15 )

24. Together: Find approximate first wrap angles.
⎛ 6 ⎞
−1
8. sin ⎜ ⎟ (in radians)
⎝ 7 ⎠
1.0297
9. tan −1 ( −15 )
Calculator gives us -1.5042, but this is not in the
first wrap. Add 2π

25. Together: Find approximate first wrap angles.
⎛ 6 ⎞
−1
8. sin ⎜ ⎟ (in radians)
⎝ 7 ⎠
1.0297
9. tan −1 ( −15 )
Calculator gives us -1.5042, but this is not in the
first wrap. Add 2π
4.7790
If the directions didn’t ask for the first wrap ...
-1.5042 would be fine.

26. HW #7
To avoid situations in which you might make mistakes
may be the biggest mistake of all.
Peter McWilliams