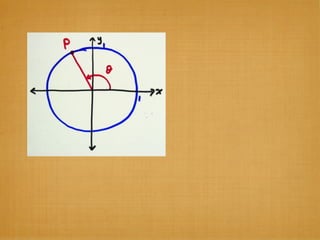
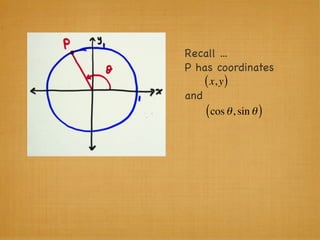
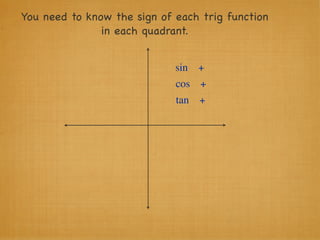
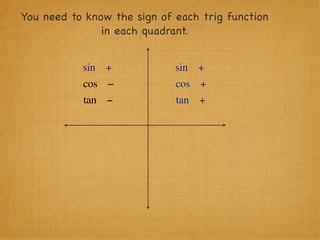
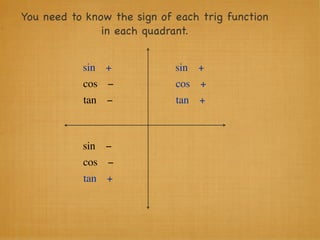
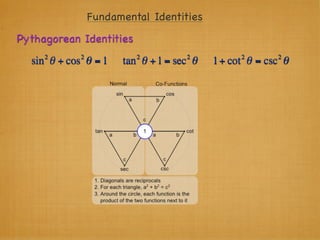
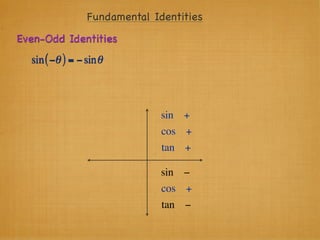
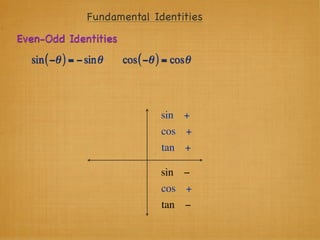
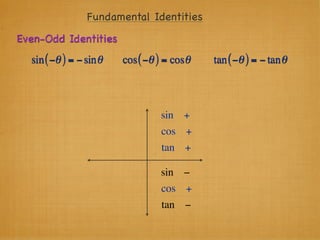
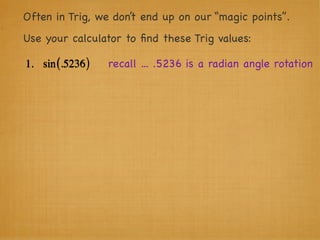
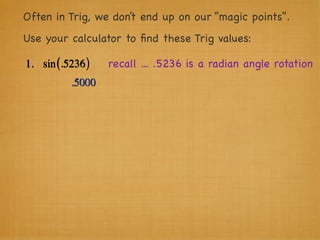
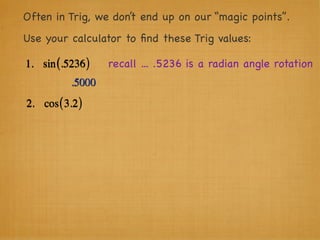
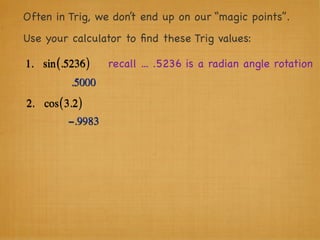
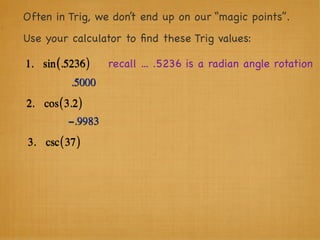
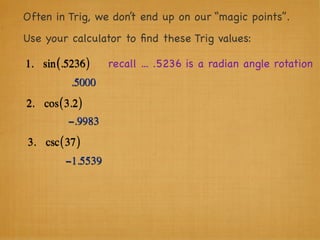
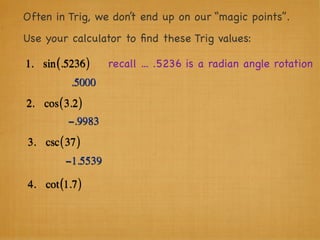
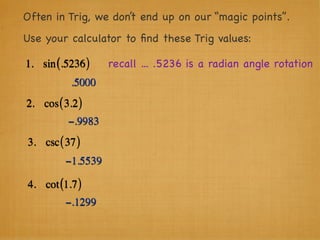
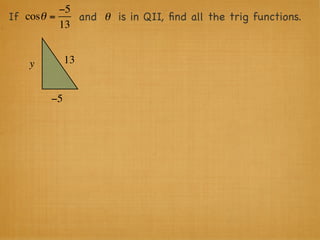The document provides examples and explanations of trigonometric functions and identities. It begins by asking students to evaluate several trigonometric expressions using a unit circle. It then reviews fundamental trigonometric identities like reciprocal, Pythagorean, and even-odd identities. It emphasizes that trigonometric values are not always at "magic points" on the unit circle and demonstrates evaluating trig functions using a calculator at arbitrary angles. It concludes by asking students to find all trig functions given the cosine of an angle in Quadrant II.

1. 5.2 Trigonometric Functions
of Real Numbers
Isaiah 40:31 But those who hope in the LORD will renew
their strength. They will soar on wings like eagles; they will
run and not grow weary, they will walk and not be faint.

3. Recall ...
P has coordinates
( x, y )
and
( cos θ , sin θ )

4. 1
sin θ = y csc θ =
y
1
cos θ = x sec θ =
x
y x
tan θ = cot θ =
x y
denominators ≠ 0

5. Groups: Using your Unit Circle, evaluate these
trigonometric expressions:

6. Groups: Using your Unit Circle, evaluate these
trigonometric expressions:
π
1. sin
3
7π
2. cos
6
11π
3. tan
4
17π
4. sec
3
17π
5. csc
2
121π
6. cot
6

7. Groups: Using your Unit Circle, evaluate these
trigonometric expressions:
π 3
1. sin
3 2
7π
2. cos
6
11π
3. tan
4
17π
4. sec
3
17π
5. csc
2
121π
6. cot
6

8. Groups: Using your Unit Circle, evaluate these
trigonometric expressions:
π 3
1. sin
3 2
7π − 3
2. cos
6 2
11π
3. tan
4
17π
4. sec
3
17π
5. csc
2
121π
6. cot
6

9. Groups: Using your Unit Circle, evaluate these
trigonometric expressions:
π 3
1. sin
3 2
7π − 3
2. cos
6 2
11π
3. tan −1
4
17π
4. sec
3
17π
5. csc
2
121π
6. cot
6

10. Groups: Using your Unit Circle, evaluate these
trigonometric expressions:
π 3
1. sin
3 2
7π − 3
2. cos
6 2
11π
3. tan −1
4
17π
4. sec 2
3
17π
5. csc
2
121π
6. cot
6

11. Groups: Using your Unit Circle, evaluate these
trigonometric expressions:
π 3
1. sin
3 2
7π − 3
2. cos
6 2
11π
3. tan −1
4
17π
4. sec 2
3
17π
5. csc 1
2
121π
6. cot
6

12. Groups: Using your Unit Circle, evaluate these
trigonometric expressions:
π 3
1. sin
3 2
7π − 3
2. cos
6 2
11π
3. tan −1
4
17π
4. sec 2
3
17π
5. csc 1
2
121π
6. cot 3
6

13. You need to know the sign of each trig function
in each quadrant.

14. You need to know the sign of each trig function
in each quadrant.
sin +
cos +
tan +

15. You need to know the sign of each trig function
in each quadrant.
sin + sin +
cos − cos +
tan − tan +

16. You need to know the sign of each trig function
in each quadrant.
sin + sin +
cos − cos +
tan − tan +
sin −
cos −
tan +

17. You need to know the sign of each trig function
in each quadrant.
sin + sin +
cos − cos +
tan − tan +
sin − sin −
cos − cos +
tan + tan −

18. You need to know the sign of each trig function
in each quadrant.
sin + sin +
cos − cos +
tan − tan +
sin − sin −
cos − cos +
tan + tan −
All Students Take Calculus

19. Fundamental Identities

20. Fundamental Identities
Reciprocal Identities

21. Fundamental Identities
Reciprocal Identities
1
csc θ =
sin θ

22. Fundamental Identities
Reciprocal Identities
1 1
csc θ = sec θ =
sin θ cos θ

23. Fundamental Identities
Reciprocal Identities
1 1 1
csc θ = sec θ = cot θ =
sin θ cos θ tan θ

24. Fundamental Identities
Pythagorean Identities

25. Fundamental Identities
Pythagorean Identities
2 2
sin θ + cos θ = 1

26. Fundamental Identities
Pythagorean Identities
2 2 2 2
sin θ + cos θ = 1 tan θ + 1 = sec θ

27. Fundamental Identities
Pythagorean Identities
2 2 2 2 2 2
sin θ + cos θ = 1 tan θ + 1 = sec θ 1+ cot θ = csc θ

28. Fundamental Identities
Pythagorean Identities
2 2 2 2 2 2
sin θ + cos θ = 1 tan θ + 1 = sec θ 1+ cot θ = csc θ

29. Fundamental Identities
Even-Odd Identities

30. Fundamental Identities
Even-Odd Identities
sin ( −θ ) = − sin θ

31. Fundamental Identities
Even-Odd Identities
sin ( −θ ) = − sin θ
sin +
cos +
tan +
sin −
cos +
tan −

32. Fundamental Identities
Even-Odd Identities
sin ( −θ ) = − sin θ cos ( −θ ) = cosθ
sin +
cos +
tan +
sin −
cos +
tan −

33. Fundamental Identities
Even-Odd Identities
sin ( −θ ) = − sin θ cos ( −θ ) = cosθ tan ( −θ ) = − tan θ
sin +
cos +
tan +
sin −
cos +
tan −

34. Fundamental Identities
Even-Odd Identities
sin ( −θ ) = − sin θ cos ( −θ ) = cosθ tan ( −θ ) = − tan θ
csc ( −θ ) = − cscθ sec ( −θ ) = secθ cot ( −θ ) = − cot θ
sin +
cos +
tan +
sin −
cos +
tan −

35. Often in Trig, we don’t end up on our “magic points”.

36. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:

37. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 )

38. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 ) recall ... .5236 is a radian angle rotation

39. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 ) recall ... .5236 is a radian angle rotation
.5000

40. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 ) recall ... .5236 is a radian angle rotation
.5000
2. cos ( 3.2 )

41. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 ) recall ... .5236 is a radian angle rotation
.5000
2. cos ( 3.2 )
−.9983

42. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 ) recall ... .5236 is a radian angle rotation
.5000
2. cos ( 3.2 )
−.9983
3. csc ( 37 )

43. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 ) recall ... .5236 is a radian angle rotation
.5000
2. cos ( 3.2 )
−.9983
3. csc ( 37 )
−1.5539

44. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 ) recall ... .5236 is a radian angle rotation
.5000
2. cos ( 3.2 )
−.9983
3. csc ( 37 )
−1.5539
4. cot (1.7 )

45. Often in Trig, we don’t end up on our “magic points”.
Use your calculator to find these Trig values:
1. sin (.5236 ) recall ... .5236 is a radian angle rotation
.5000
2. cos ( 3.2 )
−.9983
3. csc ( 37 )
−1.5539
4. cot (1.7 )
−.1299

46. −5
If cosθ = and θ is in QII, find all the trig functions.
13

47. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13
−5

48. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
−5

49. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
2 2 2
( −5 ) + y = 13
−5

50. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
2 2 2
( −5 ) + y = 13
2
−5 25 + y = 169

51. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
2 2 2
( −5 ) + y = 13
2
−5 25 + y = 169
2
y = 144

52. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
2 2 2
( −5 ) + y = 13
2
−5 25 + y = 169
2
y = 144
y = 12

53. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
2 2 2
( −5 ) + y = 13
2
−5 25 + y = 169
2
y = 144
y = 12
12
sin θ =
13

54. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
2 2 2
( −5 ) + y = 13
2
−5 25 + y = 169
2
y = 144
y = 12
12
sin θ =
13
−5
cosθ =
13

55. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
2 2 2
( −5 ) + y = 13
2
−5 25 + y = 169
2
y = 144
y = 12
12
sin θ =
13
−5
cosθ =
13
−12
tan θ =
5

56. −5
If cosθ = and θ is in QII, find all the trig functions.
13
y 13 This is easiest if we use SOHCAHTOA
2 2 2
( −5 ) + y = 13
2
−5 25 + y = 169
2
y = 144
y = 12
12 13
sin θ = cscθ =
13 12
−5 −13
cosθ = secθ =
13 5
−12 −5
tan θ = cot θ =
5 12

57. HW #3
I don’t look at myself as a basketball coach. I look at
myself as a leader who happens to coach basketball.
Mike Krzyzewski