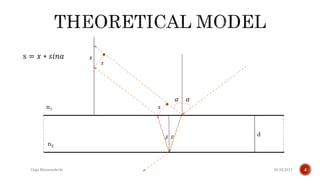
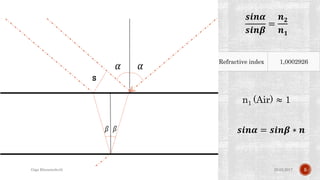
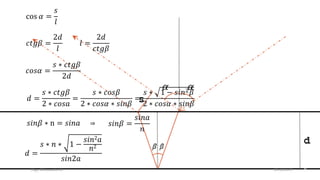
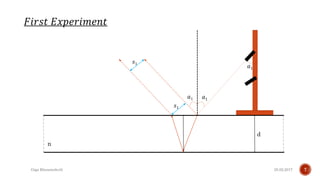
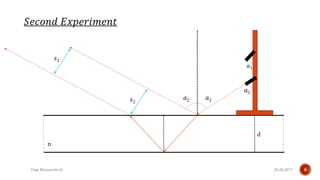
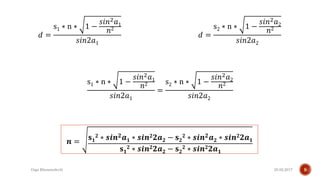
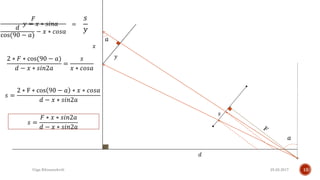
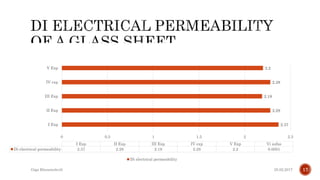
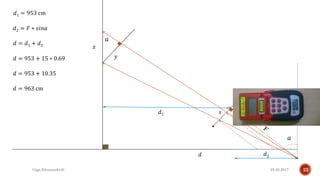
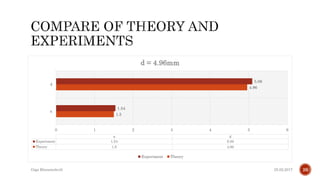
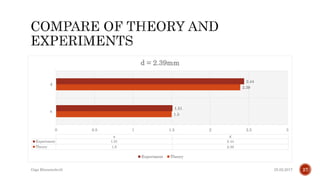
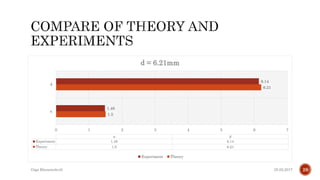
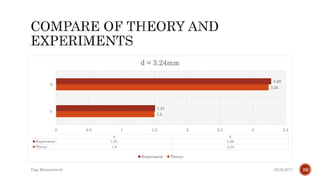
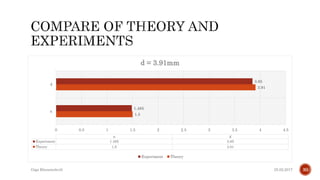
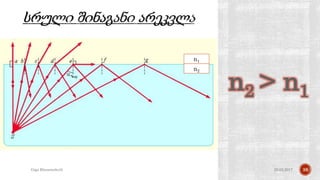
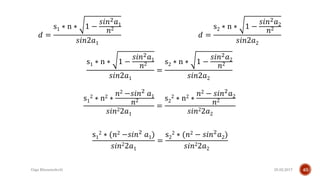
The document describes the development of a contactless calliper that uses a laser pointer to determine properties of glass sheets without contact. It outlines the theoretical model, experiments conducted, and comparison of theory to experiments. Two experiments were conducted to measure the thickness and refractive index of glass sheets. The results found a refractive index of 1.53 with a margin of error of around 4.8% due to uncertainties in measurement of angles, distances, and refractive index.