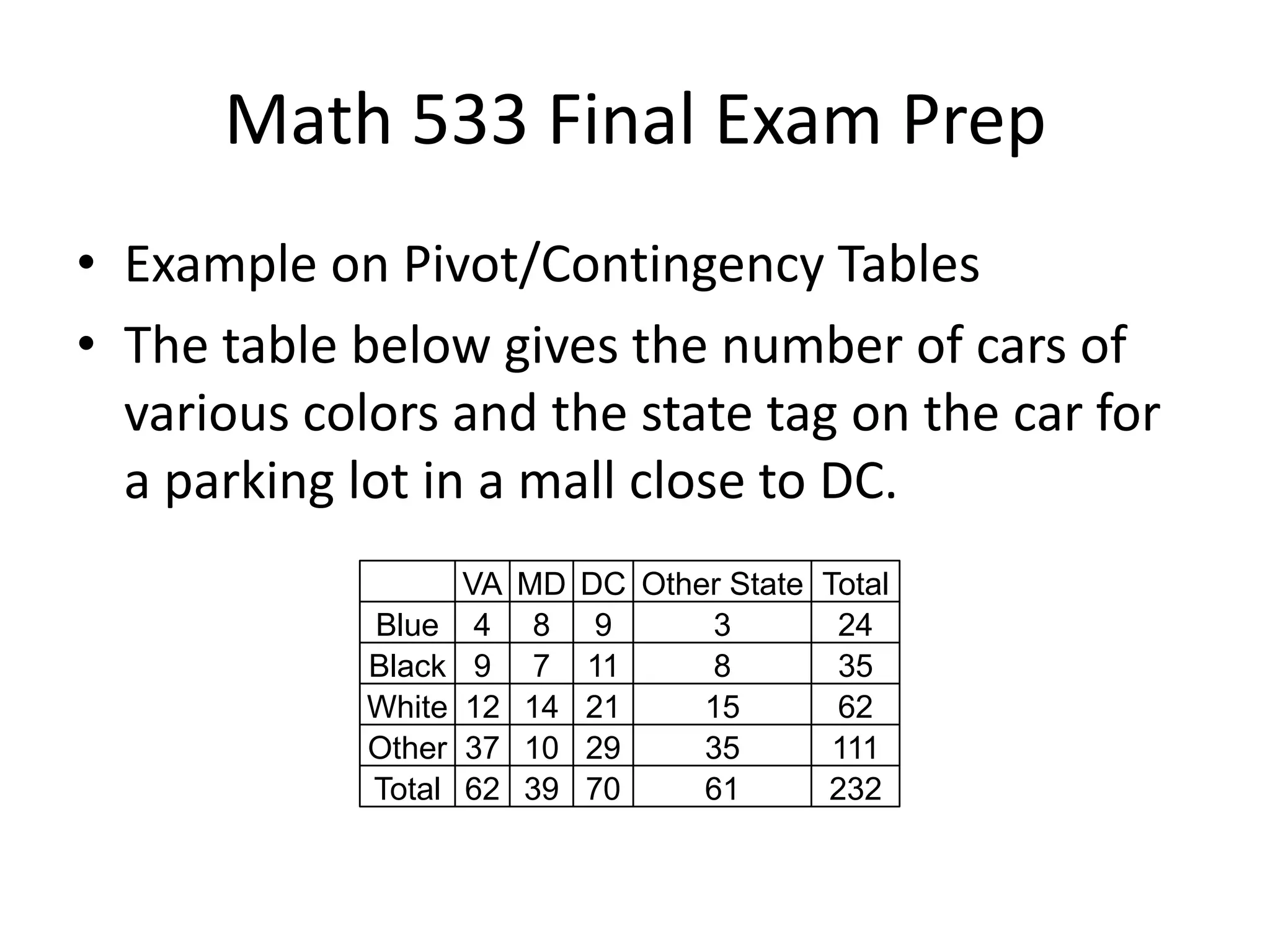
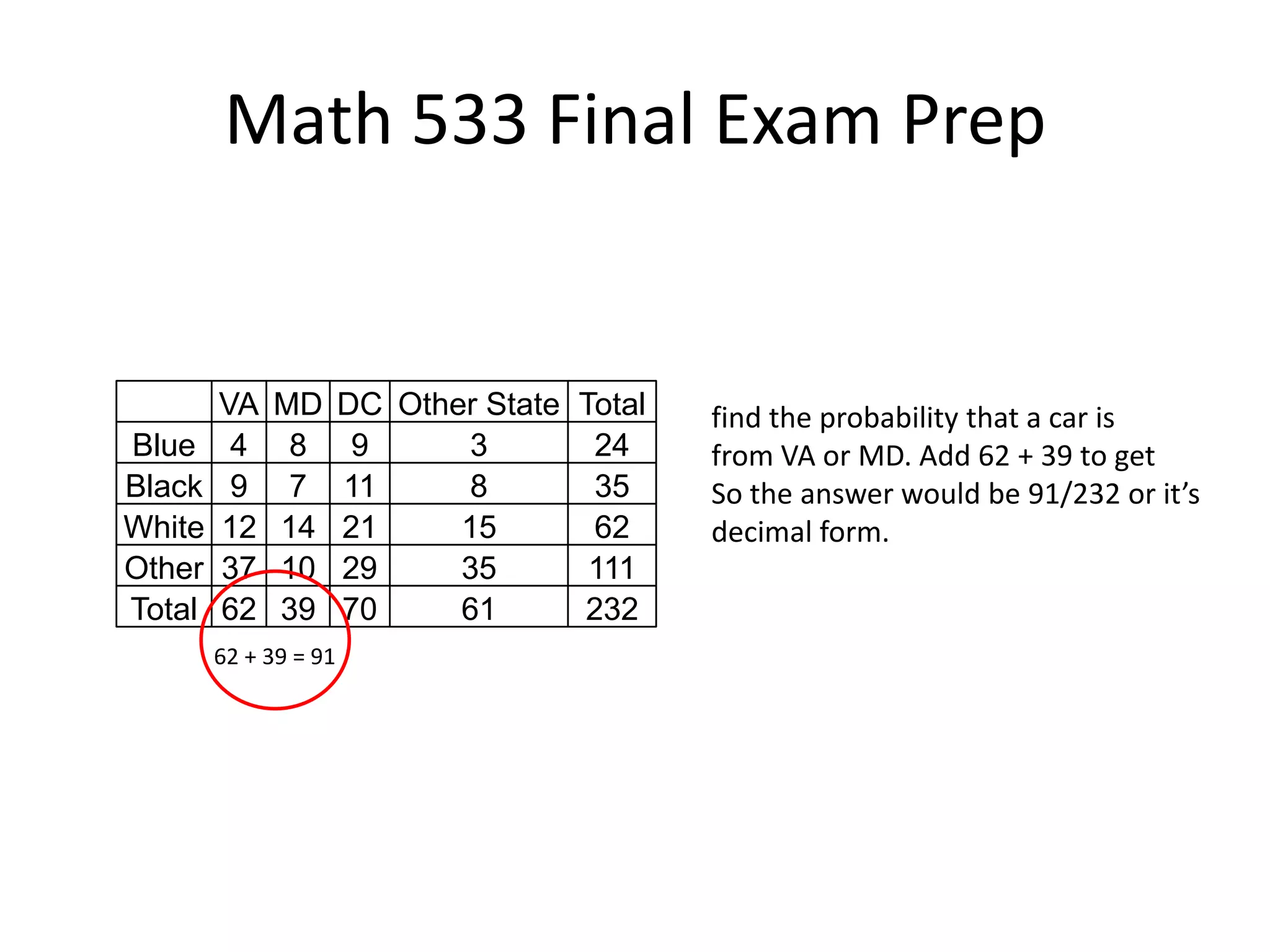
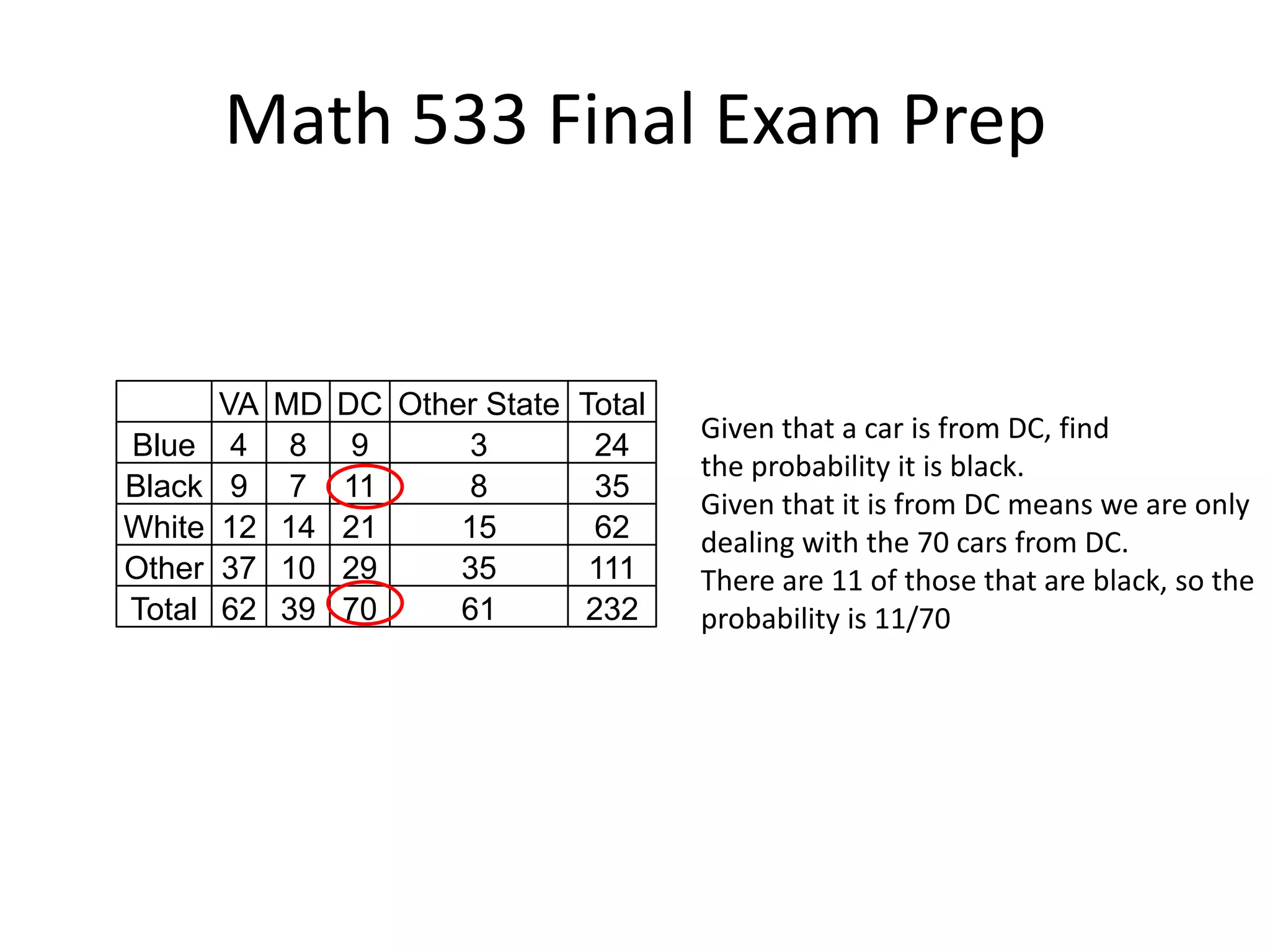
- The document provides an overview of topics that may be covered on the Math 533 final exam, including hypothesis testing, the binomial distribution, descriptive statistics, confidence intervals, and regression analysis.
- It includes examples of sample questions and worked problems for each topic to help students prepare.