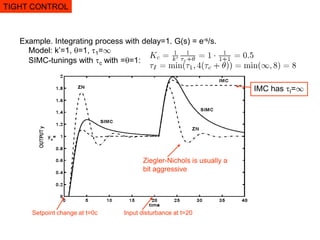
This document discusses PID controller tuning. It begins by outlining the topics that will be covered, including obtaining process models from step responses or detailed models, deriving the SIMC PID tuning rules, and special topics like integrating processes and when derivative action is needed. It then derives the SIMC PID tuning rules, which specify controller gain, integral time, and derivative time based on a process model and desired closed-loop response time. It discusses selecting the response time for tight versus smooth control and provides guidelines for minimum controller gain. Integrating processes require reducing the integral time to avoid oscillations. The document emphasizes that the SIMC rules provide a systematic approach to PID tuning.

1. Practical plantwide process
control: PID tuning
Sigurd Skogestad, NTNU

2. Part 4: PID tuning
Part 2 (4h). PID controller tuning: It pays off to be systematic!
1. Obtaining first-order plus delay models
 Open-loop step response
 From detailed model (half rule)
 From closed-loop setpoint response
2 . Derivation SIMC PID tuning rules
 Controller gain, Integral time, derivative time
3. Special topics
 Integrating processes (level control)
 Other special processes and examples
 When do we need derivative action?
 Near-optimality of SIMC PID tuning rules
 Non PID-control: Is there an advantage in using Smith Predictor? (No)
Examples

3. Operation: Decision and control layers
cs = y1s
MPC
PID
y2s
RTO
u (valves)
CV=y1; MV=y2s
CV=y2; MV=u
Min J (economics);
MV=y1s

4. PID controller
 Time domain (“ideal” PID)
 Laplace domain (“ideal”/”parallel” form)
 For our purposes. Simpler with cascade form
 Usually τD=0. Then the two forms are identical.
 Only two parameters left (Kc and τI)
 How difficult can it be to tune???
 Surprisingly difficult without systematic approach!
e

5. Trans. ASME, 64, 759-768 (Nov. 1942).
Disadvantages Ziegler-Nichols:
1.Aggressive settings
2.No tuning parameter
3.Poor for processes with large time delay (µ)
Comment:
Similar to SIMC for integrating
process with ¿c=0:
Kc = 1/k’ 1/µ
¿I = 4 µ

6. Disadvantage IMC-PID (=Lambda tuning):
1.Many rules
2.Poor disturbance response for «slow» processes (with large ¿1/µ)

7. Motivation for developing SIMC
PID tuning rules
1. The tuning rules should be well motivated, and
preferably be model-based and analytically
derived.
2. They should be simple and easy to memorize.
3. They should work well on a wide range of
processes.

8. SIMC PI tuning rule
1. Approximate process as first-order with delay (e.g., use “half rule”)
 k = process gain
 ¿1 = process time constant
 µ = process delay
2. Derive SIMC tuning rule*:
Reference: S. Skogestad, “Simple analytic rules for model reduction and PID controller design”, J.Proc.Control, Vol. 13, 291-309, 2003
(*) “Probably the best simple PID tuning rules in the world”
c ¸ - : Desired closed-loop response time (tuning parameter)
Open-loop step response
Integral time rule combines well-known rules:
IMC (Lamda-tuning): Same as SIMC for small ¿1 (¿I = ¿1)
Ziegler-Nichols: Similar to SIMC for large ¿1 (if we choose ¿c= 0; aggressive!)

9. Need a model for tuning
 Model: Dynamic effect of change in input u (MV) on
output y (CV)
 First-order + delay model for PI-control
 Second-order model for PID-control
 Recommend: Use second-order model only if ¿2>µ
MODEL

10. 1. Step response experiment
 Make step change in one u (MV) at a time
 Record the output (s) y (CV)
MODEL, Approach 1A

11. STEP IN INPUT u
RESULTING OUTPUT y
: Delay - Time where output does not change
1: Time constant - Additional time to reach
63% of final change
k =  y(∞)/ u : Steady-state gain
Δy(∞)
Δu
MODEL, Approach 1A

12. Step response integrating process
Δy
Δt
MODEL, Approach 1A

13. Shams’ method: Closed-loop setpoint response
with P-controller with about 20-40% overshoot
Kc0=1.5
Δys=1
Δyu=0.54
Δyp=0.79
tp=4.4
1. OBTAIN DATA IN RED (first overshoot
and undershoot), and then:
tp=4.4, dyp=0.79; dyu=0.54, Kc0=1.5, dys=1
dyinf = 0.45*(dyp + dyu)
Mo =(dyp -dyinf)/dyinf % Mo=overshoot (about 0.3)
b=dyinf/dys
A = 1.152*Mo^2 - 1.607*Mo + 1.0
r = 2*A*abs(b/(1-b))
%2. OBTAIN FIRST-ORDER MODEL:
k = (1/Kc0) * abs(b/(1-b))
theta = tp*[0.309 + 0.209*exp(-0.61*r)]
tau = theta*r
3. CAN THEN USE SIMC PI-rule
Example 2: Get k=0.99, theta =1.68, tau=3.03
Ref: Shamssuzzoha and Skogestad (JPC, 2010)
+ modification by C. Grimholt (Project, NTNU, 2010; see also PID-book 2012)
Δy∞
MODEL, Approach 1B

14. 2. Model reduction of more complicated model
 Start with complicated stable model on the form
 Want to get a simplified model on the form
 Most important parameter is the “effective” delay 
MODEL, Approach 2

15. MODEL, Approach 2

16. Example 1
Half rule
MODEL, Approach 2

17. original
1st-order+delay
MODEL, Approach 2

18. half rule
2
MODEL, Approach 2

19. original
1st-order+delay
2nd-order+delay
MODEL, Approach 2

20. Approximation of zeros
Alternative and improved method forf approximating zeros:
Simple Analytic PID Controller Tuning Rules Revisited
J Lee, W Cho, TF Edgar - Industrial & Engineering Chemistry Research 2014, 53 (13), pp 5038–5047
MODEL, Approach 2
To make these rules more general
(and not only applicable to the
choice c=): Replace  (time
delay) by c (desired closed-loop
response time). (6 places)
c
c
c
c
c
c

21. Derivation of SIMC-PID tuning rules
 PI-controller (based on first-order model)
 For second-order model add D-action.
For our purposes, simplest with the “series” (cascade) PID-form:
SIMC-tunings

22. Basis: Direct synthesis (IMC)
Closed-loop response to setpoint change
Idea: Specify desired response:
and from this get the controller. ……. Algebra:
SIMC-tunings

23. SIMC-tunings
NOTE: Setting the steady-state gain = 1 in T will result in integral action in the controller!

24. IMC Tuning = Direct Synthesis
Algebra:
SIMC-tunings

25. Integral time
 Found: Integral time = dominant time constant (I = 1) (IMC-rule)
 Works well for setpoint changes
 Needs to be modified (reduced) for integrating disturbances
Example. “Almost-integrating process” with disturbance at input:
G(s) = e-s/(30s+1)
Original integral time I = 30 gives poor disturbance response
Try reducing it!
g
c
d
y
u
SIMC-tunings

26. Integral Time
I = 1
Reduce I to this value:
I = 4 (c+) = 8 
SIMC-tunings
Setpoint change at t=0 Input disturbance at t=20

27. Integral time
 Want to reduce the integral time for “integrating”
processes, but to avoid “slow oscillations” we must require:
 Derivation:
 Setpoint response: Improve (get rid of overshoot) by “pre-
filtering”, y’s = f(s) ys.
SIMC-tunings
Details: See www.nt.ntnu.no/users/skoge/publications/2003/tuningPID Remark 13 II

28. Conclusion: SIMC-PID Tuning Rules
One tuning parameter: c
SIMC-tunings

29. Some insights from tuning rules
1. The effective delay θ (which limits the achievable closed-loop
time constant τc) is independent of the dominant process time
constant τ1!
 It depends on τ2/2 (PI) or τ3/2 (PID)
2. Use (close to) P-control for integrating process
 Beware of large I-action (small τI) for level control
3. Use (close to) I-control for fast process (with small time
constant τ1)
4. Parameter variations: For robustness tune at operating point
with maximum value of k’ θ = (k/τ1)θ
SIMC-tunings

30. Cascade PID -> Ideal PID

31. SIMC-tunings

32. Selection of tuning parameter c
Two main cases
1. TIGHT CONTROL: Want “fastest possible
control” subject to having good robustness
• Want tight control of active constraints (“squeeze and shift”)
2. SMOOTH CONTROL: Want “slowest possible
control” subject to acceptable disturbance rejection
• Want smooth control if fast setpoint tracking is not required, for
example, levels and unconstrained (“self-optimizing”) variables
• THERE ARE ALSO OTHER ISSUES: Input
saturation etc.
TIGHT CONTROL:
SMOOTH CONTROL:
SIMC-tunings

33. TIGHT CONTROL

34. Typical closed-loop SIMC responses with the choice c=
TIGHT CONTROL

35. Example. Integrating process with delay=1. G(s) = e-s/s.
Model: k’=1, =1, 1=1
SIMC-tunings with c with ==1:
IMC has I=1
Ziegler-Nichols is usually a
bit aggressive
Setpoint change at t=0c Input disturbance at t=20
TIGHT CONTROL

36. 1. Approximate as first-order model with k=1, 1 = 1+0.1=1.1, =0.1+0.04+0.008 = 0.148
Get SIMC PI-tunings (c=): Kc = 1 ¢ 1.1/(2¢ 0.148) = 3.71, I=min(1.1,8¢ 0.148) = 1.1
2. Approximate as second-order model with k=1, 1 = 1, 2=0.2+0.02=0.22, =0.02+0.008 = 0.028
Get SIMC PID-tunings (c=): Kc = 1 ¢ 1/(2¢ 0.028) = 17.9, I=min(1,8¢ 0.028) = 0.224, D=0.22
TIGHT CONTROL

37. Tuning for smooth control
Will derive Kc,min. From this we can get c,max using SIMC tuning rule
SMOOTH CONTROL
 Tuning parameter: c = desired closed-loop response time
 Selecting c= (“tight control”) is reasonable for cases with a relatively large
effective delay 
 Other cases: Select c >  for
 slower control
 smoother input usage
 less disturbing effect on rest of the plant
 less sensitivity to measurement noise
 better robustness
 Question: Given that we require some disturbance rejection.
 What is the largest possible value for c ?
 Or equivalently: The smallest possible value for Kc?
S. Skogestad, ``Tuning for smooth PID control with acceptable disturbance rejection'', Ind.Eng.Chem.Res, 45 (23), 7817-7822 (2006).

38. Closed-loop disturbance rejection
d0
ymax
-d0
-ymax
SMOOTH CONTROL

39. Kc
u
Minimum controller gain for PI-and PID-control:
min |c(j)| = Kc
SMOOTH CONTROL

40. Rule: Min. controller gain for
acceptable disturbance rejection:
Kc ¸ |ud|/|ymax|
often ~1 (in span-scaled variables)
SMOOTH CONTROL
|ymax| = allowed deviation for output (CV)
|ud| = required change in input (MV) for disturbance rejection (steady state)
= observed change (movement) in input from historical data

41. Rule: Kc ¸ |ud|/|ymax|
 Exception to rule: Can have lower Kc if
disturbances are handled by the integral action.
 Disturbances must occur at a frequency lower than 1/I
 Applies to: Process with short time constant (1 is small)
and no delay ( ¼ 0).
 For example, flow control
 Then I = 1 is small so integral action is “large”
SMOOTH CONTROL

42. Summary: Tuning of easy loops
 Easy loops: Small effective delay ( ¼ 0), so closed-
loop response time c (>> ) is selected for “smooth
control”
 ASSUME VARIABLES HAVE BEEN SCALED WITH
RESPECT TO THEIR SPAN SO THAT |u0/ymax| = 1
(approx.).
 Flow control: Kc=0.2, I = 1 = time constant valve
(typically, 2 to 10s; close to pure integrating!)
 Level control: Kc=2 (and no integral action)
 Other easy loops (e.g. pressure): Kc = 2, I = min(4c, 1)
 Note: Often want a tight pressure control loop (so may have
Kc=10 or larger)
SMOOTH CONTROL

43. Conclusion PID tuning
S IM C tu n in g ru le s
1 . Tig h t c o ntro l: Se le ct c=  co rres p o n d in g to
2 . S m o oth c o ntro l. S e lect Kc ¸
N o te : H a vin g s e le cte d K c (or c ), th e inte g ra l tim e I sh o u ld b e
s e lec te d a s g ive n a b o ve
3. Derivative time: Only for dominant second-order processes

44. PID: More (Special topics)
1. Integrating processes (level control)
2. Other special processes and examples
3. When do we need derivative action?
4. Near-optimality of SIMC PID tuning rules
5. Non PID-control: Is there an advantage in using Smith
Predictor? (No)
April 4-8, 2004 KFUPM-Distillation Control Course 46

45. 1. Application of smooth control
 Averaging level control
V
q
LC
Reason for having tank is to smoothen disturbances in concentration and flow.
Tight level control is not desired: gives no “smoothening” of flow disturbances.
SMOOTH CONTROL LEVEL CONTROL
If you insist on integral action
then this value avoids cycling
Proof: 1. Let
|u0| = |q0| – expected flow change [m3/s] (input disturbance)
|ymax| = |Vmax| - largest allowed variation in level [m3]
Minimum controller gain for acceptable disturbance rejection:
Kc ¸ Kc,min = |u0|/|ymax| = |q0| / |Vmax|
2. From the material balance (dV/dt = q – qout), the model is g(s)=k’/s with k’=1.
Select Kc=Kc,min. SIMC-Integral time for integrating process:
I = 4 / (k’ Kc) = 4 |Vmax| / | q0| = 4 ¢ residence time
provided tank is nominally half full and q0 is equal to the nominal flow.

46. More on level control
 Level control often causes problems
 Typical story:
 Level loop starts oscillating
 Operator detunes by decreasing controller gain
 Level loop oscillates even more
 ......
 ???
 Explanation: Level is by itself unstable and
requires control.
LEVEL CONTROL

47. Level control: Can have both
fast and slow oscillations
 Slow oscillations (Kc too low): P > 3¿I
 Fast oscillations (Kc too high): P < 3¿I
Here: Consider the less common slow oscillations
LEVEL CONTROL

48. How avoid oscillating levels?
LEVEL CONTROL
• S im p le st: U se P -c o n tro l o n ly (n o in te g ra l a c tio n )
• If yo u in s is t o n in te g ra l a c tio n , th e n m a k e su re
th e c o n tro lle r g a in is su ffic ie n tly la rg e
• If yo u h a ve a le ve l lo o p th a t is o sc illa tin g th e n
u se S ig u rd s ru le (c an be d erive d):
T o a vo id o sc illatio ns , inc re as e K c ¢I by fa cto r
f= 0 .1 ¢(P 0/I0)2
w h e re
P 0 = p e rio d o f o sc illatio ns [s ]
I0 = o rig ina l inte gra l tim e [s]
0.1 ¼ 1/2

49. Case study oscillating level
 We were called upon to solve a problem with
oscillations in a distillation column
 Closer analysis: Problem was oscillating reboiler
level in upstream column
 Use of Sigurd’s rule solved the problem
LEVEL CONTROL

50. LEVEL CONTROL

51. One tuning parameter: c
SIMC-tunings
2. Some special cases

52. Another special case: IPZ process
 IPZ-process may represent response from steam flow to pressure
 Rule T2:
 SIMC-tunings
These tunings turn out to be almost identical to the tunings given on page 104-106 in the Ph.D.
thesis by O. Slatteke, Lund Univ., 2006 and K. Forsman, "Reglerteknik for processindustrien",
Studentlitteratur, 2005.
SIMC-tunings

53. Note: Derivative action is commonly used for temperature control loops.
Select D equal to 2 = time constant of temperature sensor
3. Derivative action?

54. Time delay process: Setpoint and disturbance responses same + input response same
θ=1
Optimal PI*
Pure time delay process: “Minor”
improvement by adding D-action*
* D-action (ID-control) is equivalent to PI-control (with ¿ >0)
= I-control

55. Pure time delay process

56. ) Two alternative “Improved SIMC”-rules
Alt. 1. Improved PI-rule (iSIMC-PI): Add θ/3 to 1
Alt. 2. Improved PID-rule (iSIMC-PID): Add θ/3 to 2
iSIMC-PI and iSIMC-PID are identical for pure delay process (¿1=0)
iSIMC-PID is better for integrating process

57. Integrating process
0 10 20 30 40
0
1
2
3
op t P I D
SI M C P I
i SI M C P I D
op t P I
do di
G(s) = 1
s
e− s
Time, t
Out
put
s,
y
0 10 20 30 40
− 1.5
− 1
− 0.5
0
0.5
op t P I D
op t P I
S
I
M
C
P
I
i SI M C P I D
Time, t
Input
s,
u

58.  Multiobjective. Tradeoff between
 Output performance
 Robustness
 Input usage
 Noise sensitivity
High controller gain (“tight control”)
Low controller gain (“smooth control”)
• Quantification
– Output performance:
• Rise time, overshoot, settling time
• IAE or ISE for setpoint/disturbance
– Robustness: Ms, Mt, GM, PM, Delay margin, …
– Input usage: ||KSGd||, TV(u) for step response
– Noise sensitivity: ||KS||, etc.
Ms = peak sensitivity
J = avg. IAE for
setpoint/disturbance
Our choice:
4. Optimality of SIMC rules
How good are the SIMC-rules compared to optimal PI/PID?

59. 2 4 6 8 10
− 0.5
0
0.5
1
1.5
I AEdo
do
Time, t
Error,
e(t
)
2 4 6 8 10
− 0.5
0
0.5
1
1.5
I AEdi
di
Time, t
Error,
e(t
)
Performance (J):
di do
ysp K (s) G(s) y
−
e u + +

60. Robustness (Ms):

61. JIAE vs. Ms for optimal PI/PID (-) and SIMC (¢¢) for 4 processes
CONCLUSION: SIMC almost «Pareto-optimal»
Note: “PID” weightings used for JIAE

62. 5. Better with IMC, Smith
Predictor or MPC?
 Suprisingly, the answer is:
 NO, worse

63. The Smith Predictor
Where K is a “normal” controller
IMC controller
Special case of Smith Predictor where K is a PI controller with the parameters
Kc = ¿1/(k ¿c)
¿I = ¿1
Kc =0
Ki = Kc/¿I = 1/¿c
¿1 > 0 ¿1 = 0
(I-controller)

64. Comparison of J vs. Ms for optimal and SIMC for 4 processes
CONCLUSION: i-SIMC is generally better than IMC & SP!

65. Step response, SP and PI
g(s) = k e¡ s
s+ 1
µ = 1
y
time time time
µ= 0:57
µ= 1:43
Smith Predictor: Sensitive to both
positive and negative delay error
SP = Smith Predictor

66.  Reason: SP & IMC can have multiple GM, PM, DM

67.  CONCLUSION
 Well-tuned PI or PID is better than Smith Predictor
or IMC!!
 Especially for integrating processes