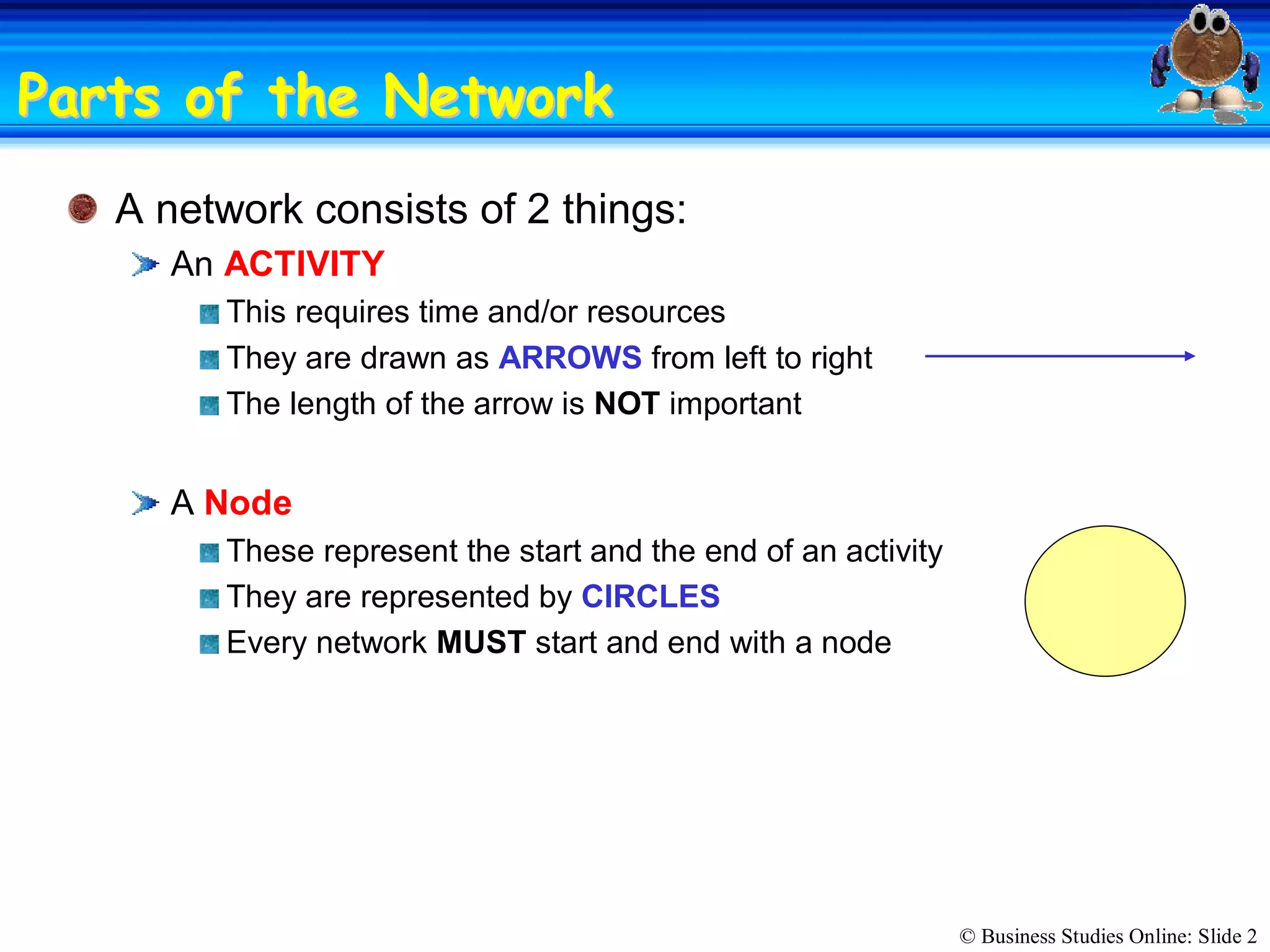
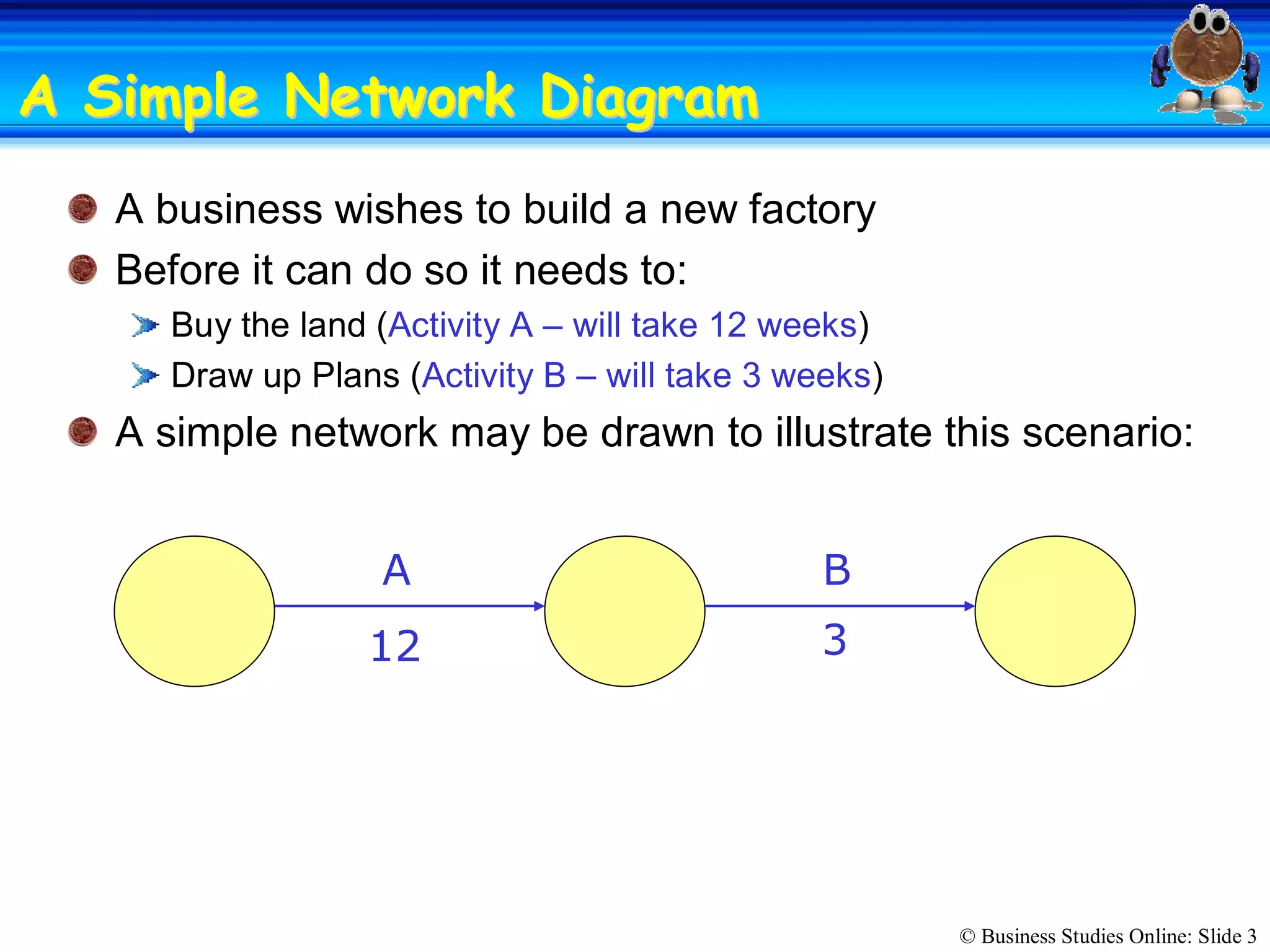
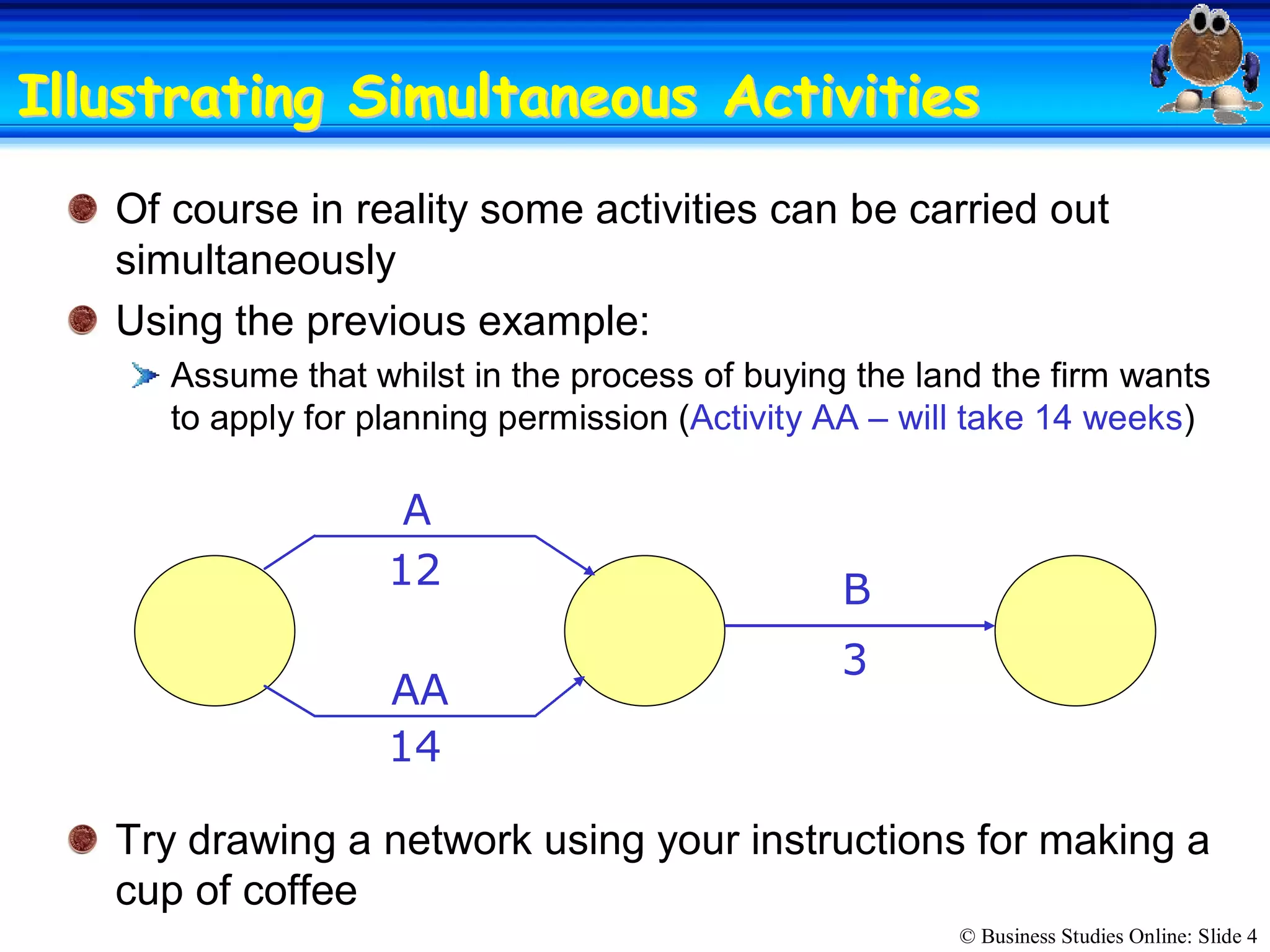
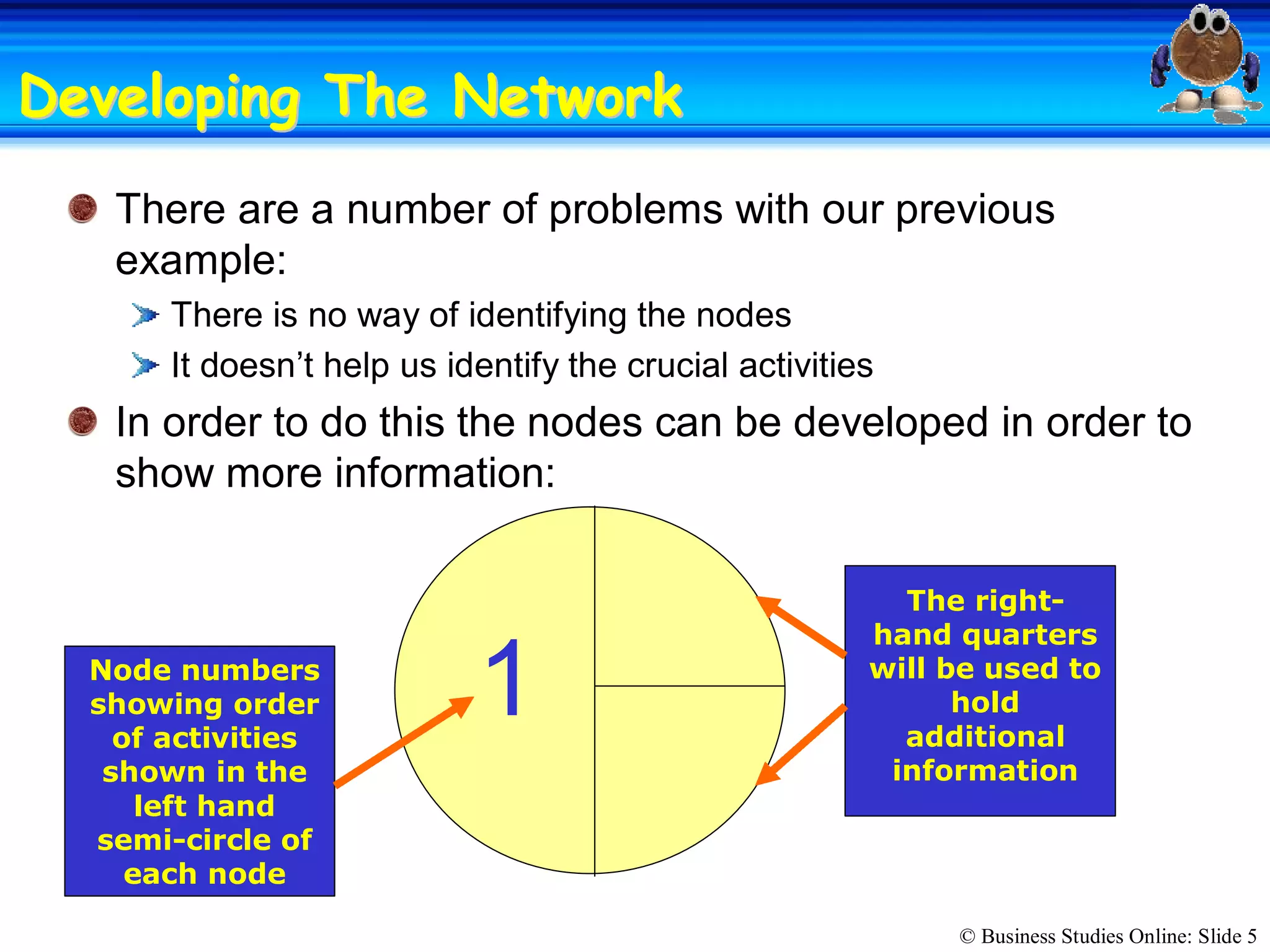
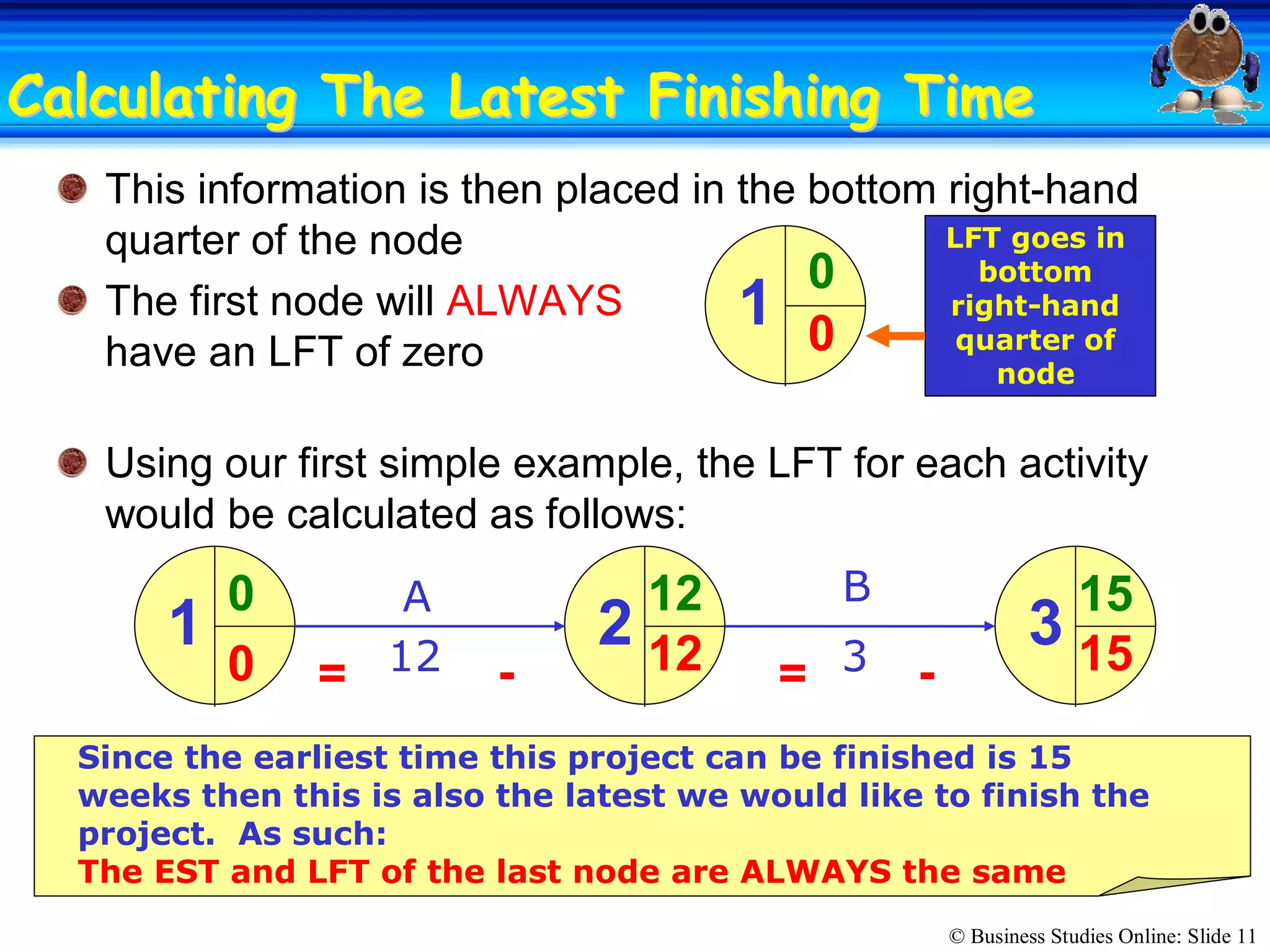
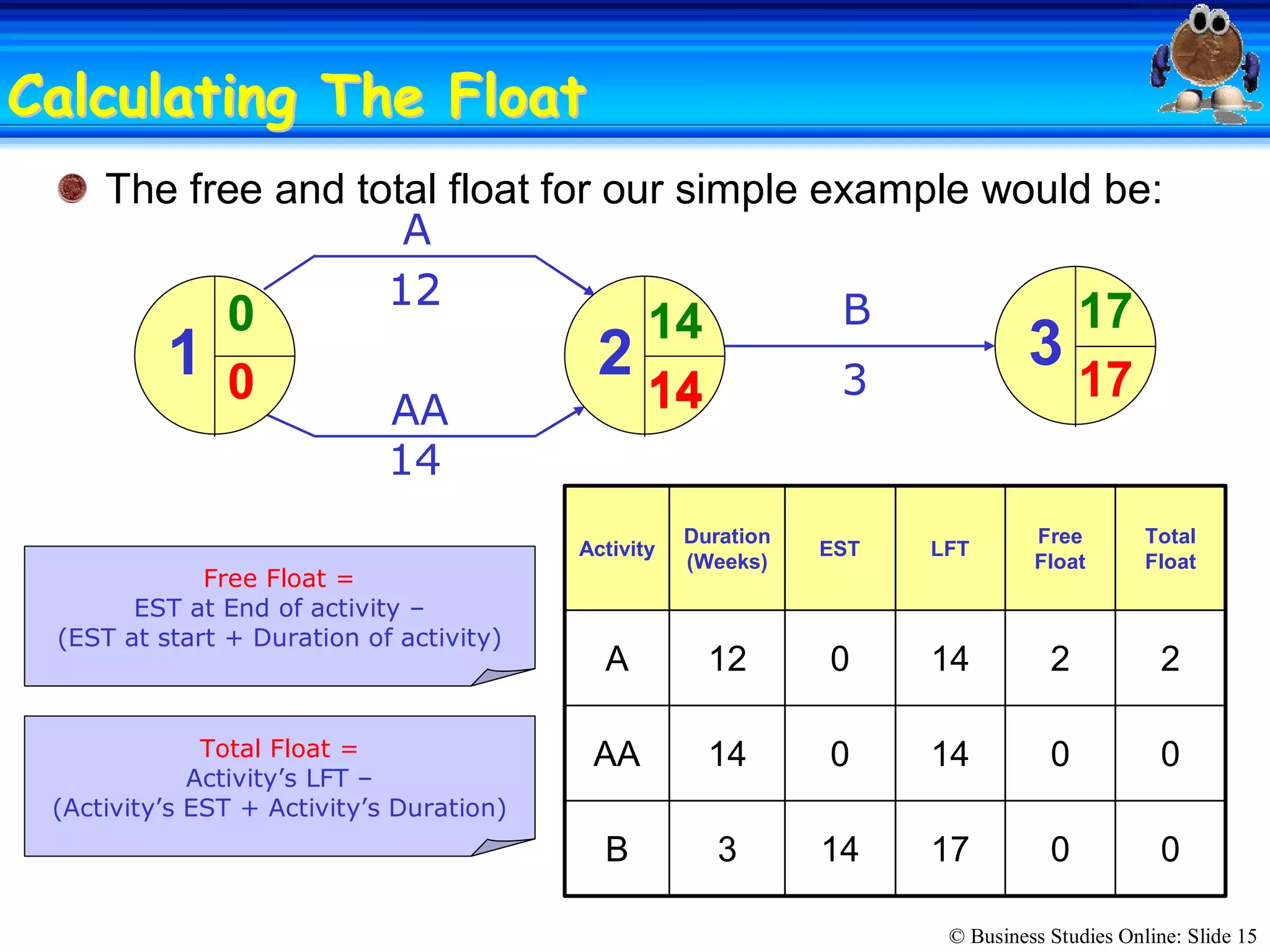
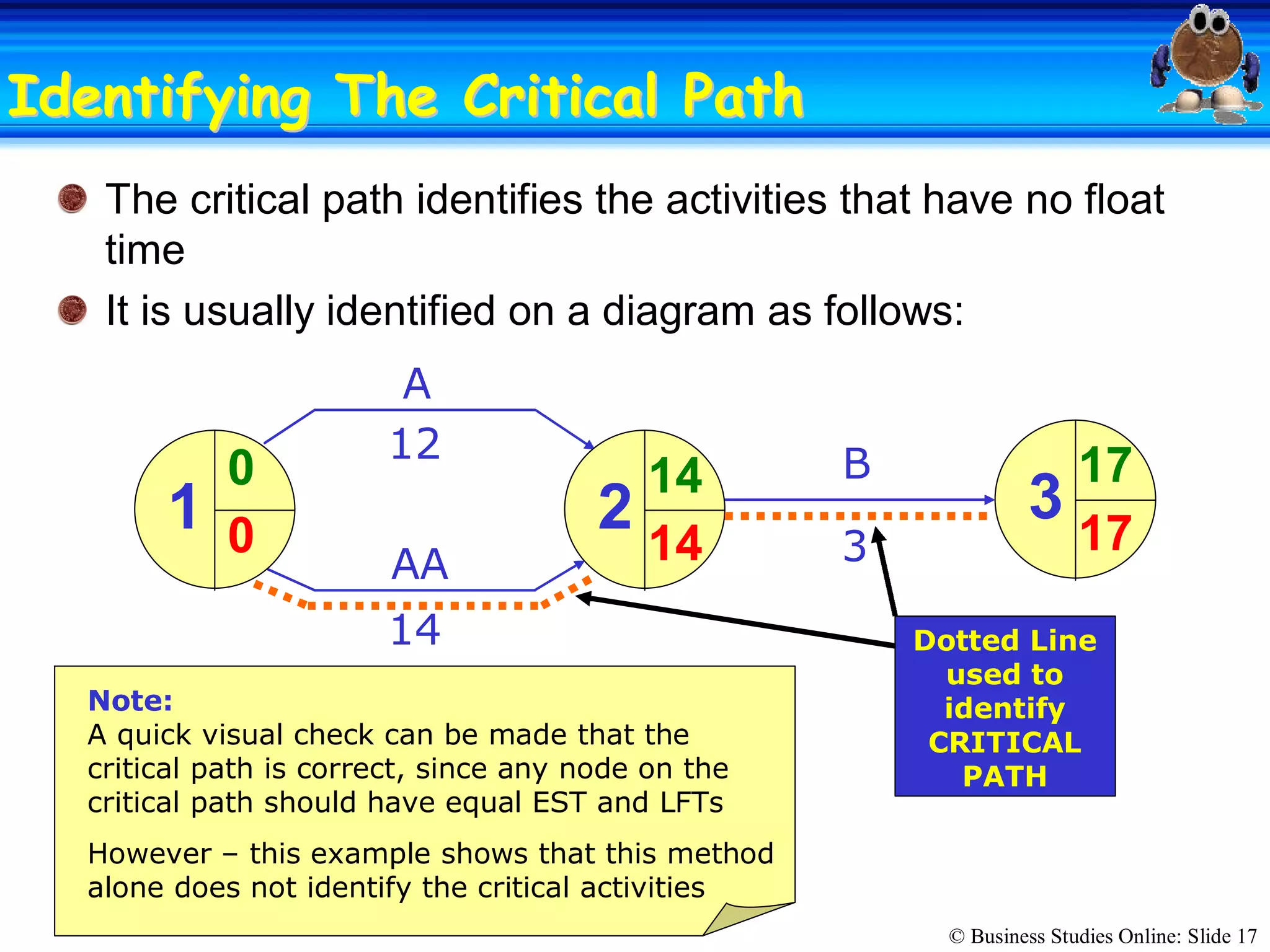
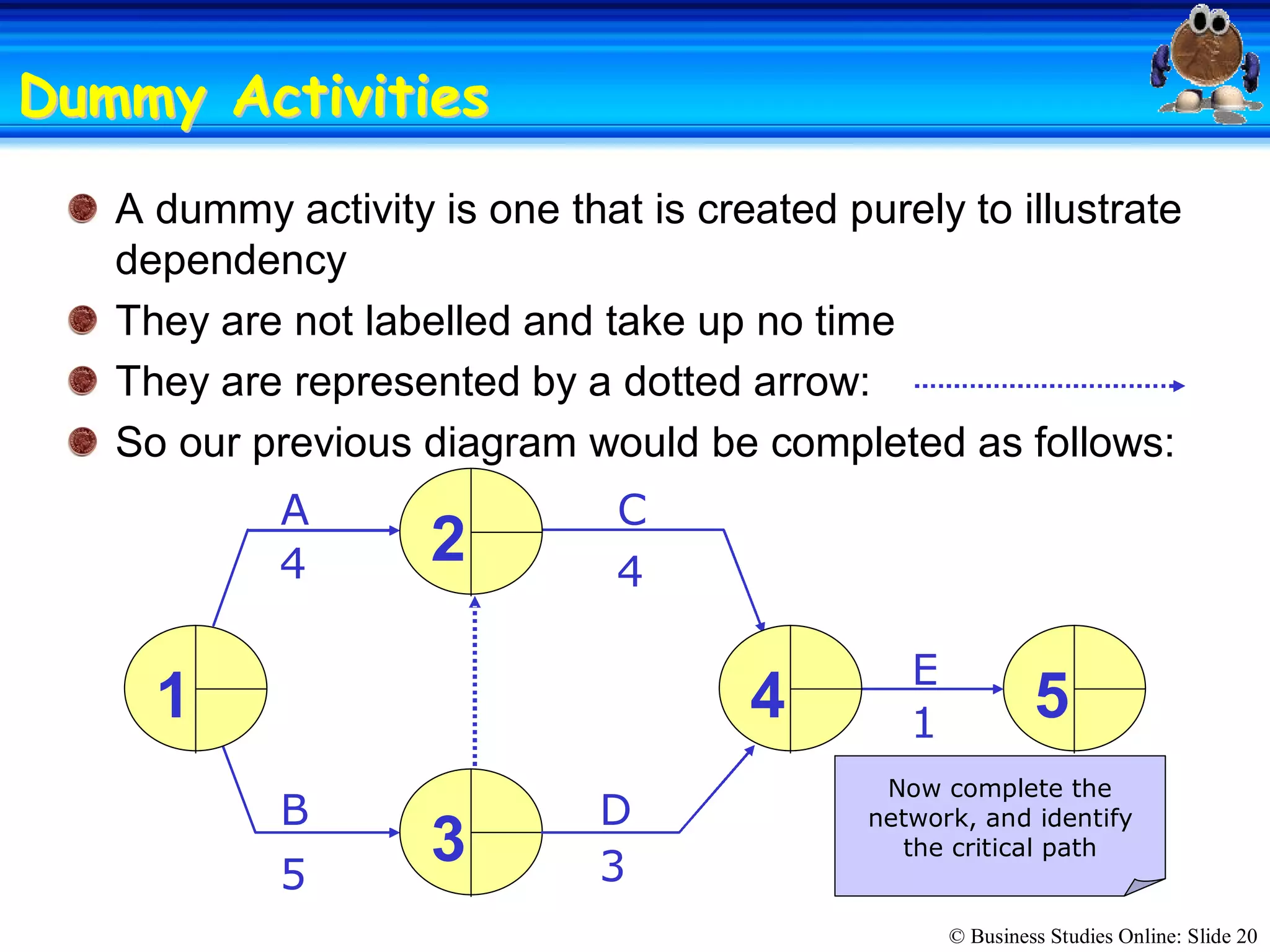
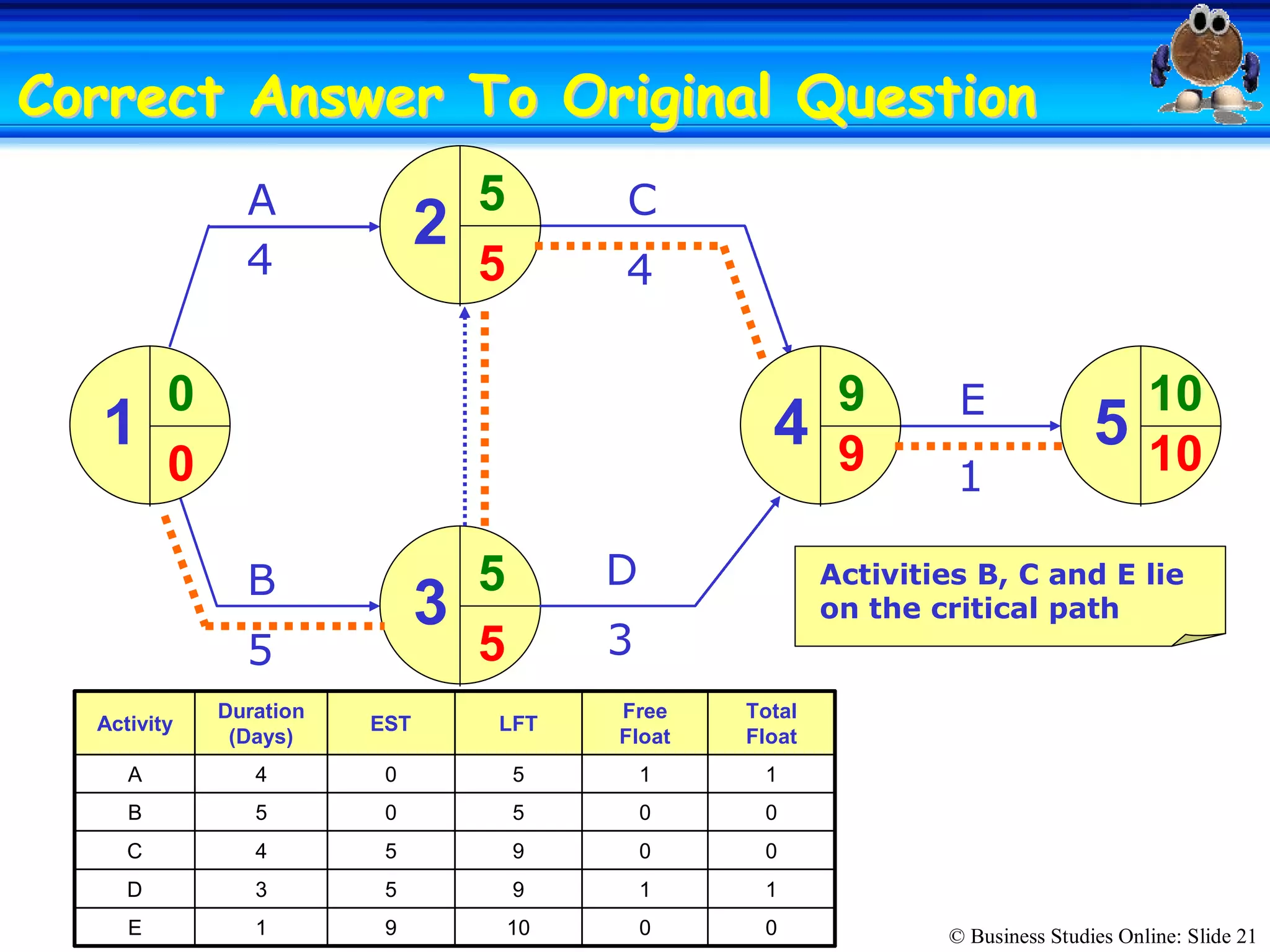
The passage discusses the importance of copyright and how it protects original works of authorship such as books, music, art, and movies. Copyright gives the creator exclusive rights to make copies, distribute copies, publicly display, or publicly perform their work. Infringing on someone's copyright by copying, distributing, or displaying their work without permission is illegal and can result in civil lawsuits and criminal prosecution.