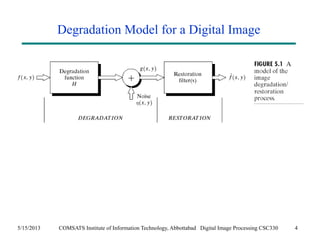
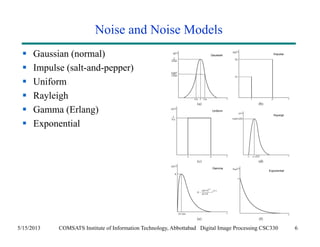
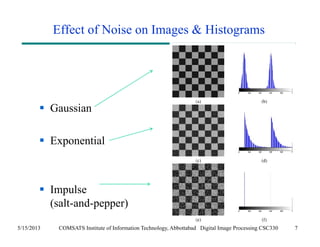
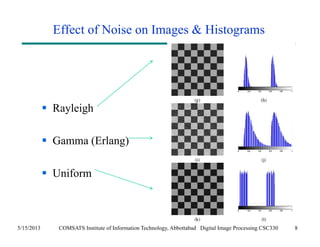
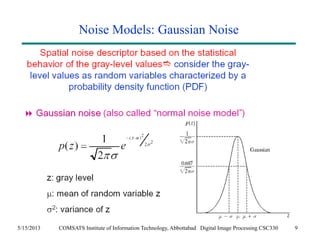
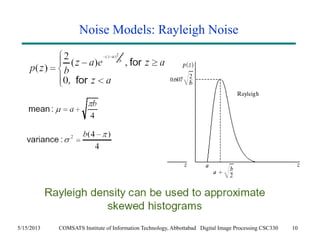
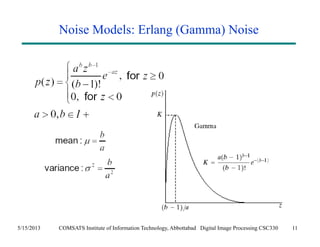
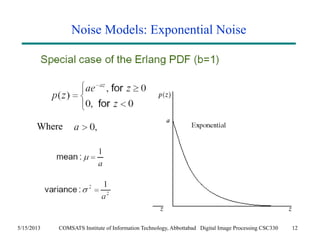
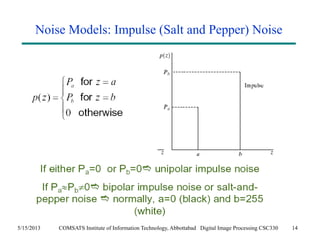
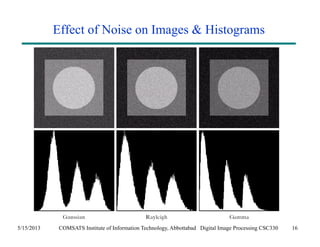
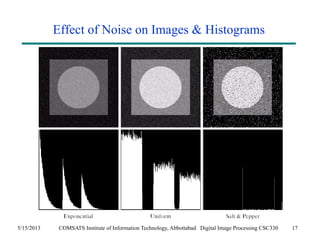
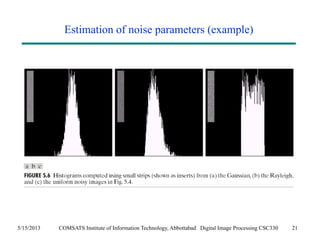
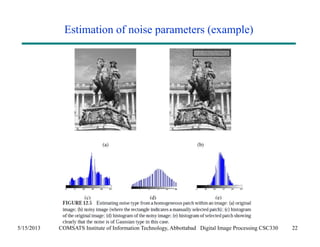
The document discusses noise models and methods for removing additive noise from digital images. It describes several types of noise that can affect images, such as Gaussian, impulse, uniform, Rayleigh, gamma and exponential noise. It also presents various noise filters that can be used to remove noise, including mean filters like arithmetic, geometric and harmonic filters, and order statistics filters such as median, max, min and midpoint filters. The filters aim to reduce noise while retaining image detail as much as possible.

1. Digital Image Processing
Image Restoration
Noise models and additive noise removal
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 1

2. Image Restoration
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 2

3. Image Restoration
 What is noise (in the context of image processing) and how can it
be modeled?
 What are the main types of noise that may affect an image?
 What are the possible solutions?
 Subjective Vs Objective (Enhancement Vs Restoration)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 3

4. Degradation Model for a Digital Image
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 4

5. Noise Models
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 5

6. Noise and Noise Models
 Gaussian (normal)
 Impulse (salt-and-pepper)
 Uniform
 Rayleigh
 Gamma (Erlang)
 Exponential
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 6

7. Effect of Noise on Images & Histograms
 Gaussian
 Exponential
 Impulse
(salt-and-pepper)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 7

8. Effect of Noise on Images & Histograms
 Rayleigh
 Gamma (Erlang)
 Uniform
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 8

9. Noise Models: Gaussian Noise
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 9

10. Noise Models: Rayleigh Noise
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 10

11. Noise Models: Erlang (Gamma) Noise
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 11

12. Noise Models: Exponential Noise
Where
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 12

13. Noise Models: Uniform Noise
1 , if
  
 
0 otherwise
 
p ( z )
b a
a z b
The mean and variance are
given by



a b 2 b  a
, ( )
12

  
2
2

5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 13

14. Noise Models: Impulse (Salt and Pepper) Noise
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 14

15. Effect of Noise on Images & Histograms
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 15

16. Effect of Noise on Images & Histograms
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 16

17. Effect of Noise on Images & Histograms
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 17

18. Periodic Noise (Example)
 Spatially Dependent Case
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 18

19. Applicability of various noise models
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 19

20. Estimation of noise parameters
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 20

21. Estimation of noise parameters (example)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 21

22. Estimation of noise parameters (example)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 22

23. Estimation of noise parameters
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 23

24. Restoration of noise-only degradation
Filters to be considered
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 24

25. Mean Filters: Arithmetic mean filter
Causes a certain amount of blurring (proportional to the window size) to
the image, thereby reducing the effects of noise.
Can be used to reduce noise of different types, but works best for Gaussian,
uniform, or Erlang noise.
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 25

26. Mean Filters: Geometric mean filter
– A variation of the arithmetic mean filter
– Primarily used on images with Gaussian noise
– Retains image detail better than the arithmetic mean
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 26

27. Mean Filters: Harmonic mean filter
Harmonic mean filter
– Another variation of the arithmetic mean filter
– Useful for images with Gaussian or salt noise
– Black pixels (pepper noise) are not filtered
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 27

28. Arithmetic and geometric mean filters (example)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 28

29. Mean Filters: Harmonic mean filter
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 29

30. Mean Filters: Harmonic mean filter
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 30

31. Mean Filters: Contra-harmonic mean filter
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 31

32. Classification of contra-harmonic filter applications
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 32

33. Contra-harmonic mean filter (example)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 33

34. Contra-harmonic mean filter (example)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 34

35. Rank / Order / Order Statistics Filters
– Known as Rank filters, Order filters OR Order Statistics filters
– Operate on a neighborhood around a reference pixel by
ordering (ranking) the pixel values and then performing an
operation on those ordered values to obtain the new value for
the reference pixel
– They perform very well in the presence of salt and pepper noise
but are more computationally expensive as compared to mean
filters
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 35

36. Rank / Order Statistics Filters: Median filter
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 36

37. Rank / Order Statistics Filters: Median filter
– Most popular and useful of the rank filters.
– It works by selecting the middle pixel value from the ordered set
of values within the m × n neighborhood (W) around the
reference pixel.
• If mn is an even number, the arithmetic average of the two
values closest to the middle of the ordered set is used
instead.
– Many variants, extensions, and optimized implementations in
the literature.
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 37

38. Median filter (Example)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 38

39. Rank / Order Statistics Filters: Max and Min filter
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 39

40. Rank / Order Statistics Filters: Max and Min filter
– Max filter also known as 100th percentile filter
– Min filter also known as zeroth percentile filter
– Max filter helps in removing pepper noise
– Min filter helps in removing salt noise
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 40

41. Max and Min filter (Example)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 41

42. Rank / Order Statistics Filters: Midpoint filter
– Calculates the average of the highest and lowest pixel values
within a window
– What would it do with salt and pepper noise ?
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 42

43. Midpoint filter (Example)
5/15/2013 COMSATS Institute of Information Technology, Abbottabad Digital Image Processing CSC330 43