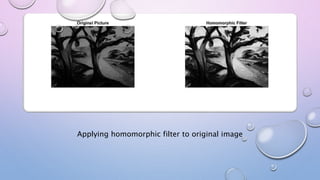
Homomorphic filtering is a technique used to remove multiplicative noise from images by transforming the image into the logarithmic domain, where the multiplicative components become additive. This allows the use of linear filters to separate the illumination and reflectance components, with a high-pass filter used to remove low-frequency illumination variations while preserving high-frequency reflectance edges. The filtered image is then transformed back to restore the original domain. Homomorphic filtering is commonly used to correct non-uniform illumination and simultaneously enhance contrast in grayscale images.

1. HOMOMORPHIC FILTERING

2. INTRODUCTION
 Homomorphic filtering is a generalized technique for signal and image processing, involving a
nonlinear mapping to a different domain in which linear filter techniques are applied, followed by
mapping back to the original domain.
 Homomorphic filter is sometimes used for image enhancement. It simultaneously normalizes the
brightness across an image and increases contrast.
 Homomorphic filtering is one such technique for removing multiplicative noise that has certain
characteristics.
 Homomorphic filtering is most commonly used for correcting non-uniform illumination in images.
 Homomorphic filtering can be used for improving the appearance of a grayscale image by
simultaneous intensity range compression (illumination) and contrast enhancement (reflection).

3. OPERATION
The illumination-reflectance model of image formation says that the intensity at any pixel, which is the
amount of light reflected by a point on the object, is the product of the illumination of the scene and the
reflectance of the object(s) in the scene, i.e.,
I(x,y)=L(x,y) * R(x,y)
where I is the image, L is scene illumination, and R is scene reflectance.
Illumination typically varies slowly across the image as compared to reflectance which can change quite
abruptly at object edges. This difference is the key to separating out the illumination component from the
reflectance component. In homomorphic filtering we first transform the multiplicative components to
additive components by moving to the log domain.
ln(I(x,y))=ln(L(x,y) R(x,y))
ln(I(x,y))=ln(L(x,y))+ln(R(x,y))

4. In DFT H(u,v) (DFT) -1 expI 𝑥, 𝑦 g 𝑥, 𝑦
OPERATION
Then we use a high-pass filter in the log domain to remove the low-frequency illumination component
while preserving the high-frequency reflectance component. The basic steps in homomorphic filtering
are shown in the diagram below:
The illumination component of an image generally is characterized by slow spatial variations,
while the reflectance component tends to vary abruptly, particularly at junction of dissimilar
objects.

5. Applying homomorphic filter to original image

6. HISTOGRAM EQUALIZATION
• Histogram equalization is a method in image processing of contrast adjustment using
the image's histogram.
• The method is useful in images with backgrounds and foregrounds that are both bright or both
dark.
• A key advantage of the method is that it is a fairly straight forward technique and
an invertible operator. So in theory, if the histogram equalization function is known, then the
original histogram can be recovered.
• A disadvantage of the method is that it is indiscriminate. It may increase the contrast of
background noise, while decreasing the usable signal.
• Histogram equalization often produces unrealistic effects in photographs; however it is very
useful for scientific images like thermal, satellite or x-ray images.

7. HISTOGRAM EQUALIZED IMAGE

8. References:
1. GonzalezandWoods,DigitalImageProcessing,PearsonEducation,3/e,(2008)
2. https://blogs.mathworks.com/steve/2013/06/25/homomorphic-filtering-part-1/
3. https://en.wikipedia.org/wiki/homomorphic_filtering

9. THANK YOU