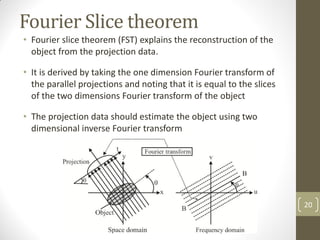
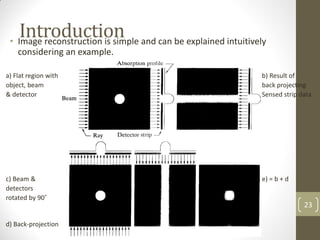
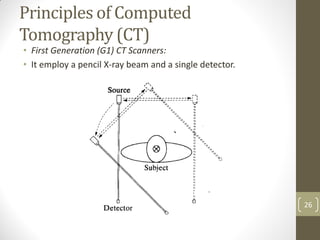
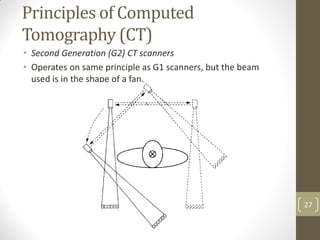
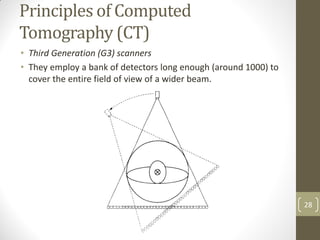
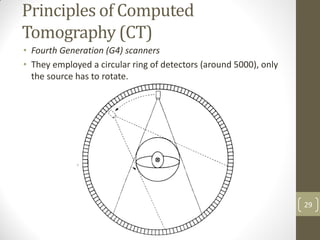
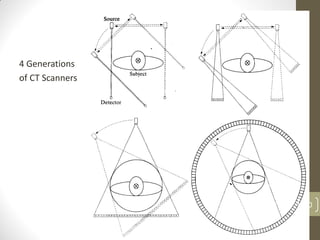
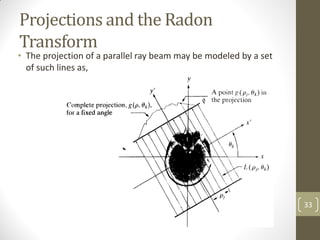
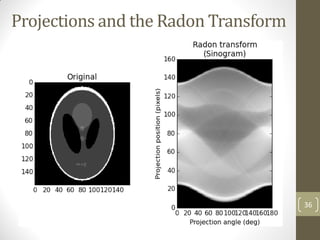
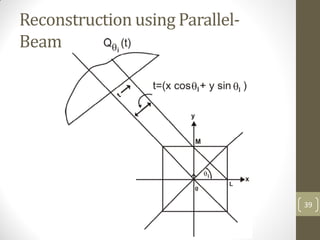
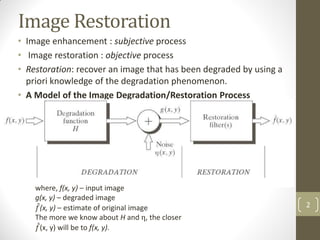
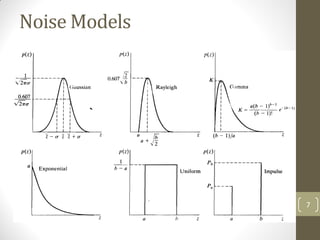
The document discusses image restoration and reconstruction techniques. It covers topics like image restoration models, noise models, spatial filtering, inverse filtering, Wiener filtering, Fourier slice theorem, computed tomography principles, Radon transform, and filtered backprojection reconstruction. As an example, it derives the analytical expression for the projection of a circular object using the Radon transform, showing that the projection is independent of angle and equals 2Ar√(r2-ρ2) when ρ ≤ r.

1. DIGITALIMAGEPROCESSING
IMAGE
RESTORATION AND
RECONSTRUCTION
by
Dr. K. M. Bhurchandi

2. Image Restoration
• Image enhancement : subjective process
• Image restoration : objective process
• Restoration: recover an image that has been degraded by using a
priori knowledge of the degradation phenomenon.
• A Model of the Image Degradation/Restoration Process
2
where, f(x, y) – input image
g(x, y) – degraded image
𝑓(x, y) – estimate of original image
The more we know about H and η, the closer
𝑓(x, y) will be to f(x, y).

3. • If H is a linear, position-invariant process, then the degraded
image is given in the spatial domain by:
• Where, h(x, y) is the spatial representation of the degraded
function H.
• Frequency domain representation of the above equation will
be:
3

4. Noise Models
• The noise component may be characterized by a PDF. The
most common PDFs found in image processing applications
are as below:
i) Gaussian Noise: Used in spatial and frequency domain. The
PDF of a Gaussian random variable, z, is given by
ii) Rayleigh Noise: The PDF of Rayleigh noise is given by
Mean Variance 4

5. Noise Models
iii) Erlang (Gamma) Noise: The PDF of Erlang noise is given by:
where, a > 0, b is a positive integer.
Mean Variance
iv) Exponential Noise: The PDF of exponential noise is given by:
where, a > 0
Mean Variance
This is a special case of erlang PDF with b = 1
5

6. Noise Models
v) Uniform Noise: The PDF of uniform noise is given by:
Mean Variance
vi) Impulse (salt and pepper) noise: The PDF of impulse (bipolar)
noise is given by:
If b > a, intensity b will appear as a light dot in the image.
Conversely, level a will appear like a dark dot.
If either Pa or Pb is zero, the impulse noise is called unipolar.
6

7. Noise Models
7

8. Images and histograms resulting from
addition of various noises to the image
8

9. 9

10. Periodic Noise
• Typically comes from electrical and electromechanical interference
during image acquisition
• Can be reduced significantly using frequency domain filtering
10
Image Corrupted by
Sinusoidal Noise
Spectrum (Each pair of conjugate
impulse corresponds to one sine wave).

11. Restoration in presence of noise
only- Spatial Filtering
• When the only degradation present in an image is noise
The corrupted image is g(x, y) = f(x, y) + η(x, y)
And
G(u, v) = F(u, v) + N(u, v)
• When only additive noise present
• Mean Filters
• Arithmetic mean
𝑓 𝑥, 𝑦 =
1
𝑚𝑛
𝑔(𝑠, 𝑡)
𝑠,𝑡∈𝑆(𝑥,𝑦)
• Geometric mean
𝑓 𝑥, 𝑦 = 𝑔 𝑠, 𝑡
𝑠,𝑡∈𝑆 𝑥,𝑦
1
𝑚𝑛
11

12. • Harmonic mean
𝑓 𝑥, 𝑦 =
𝑚𝑛
1
𝑔(𝑠,𝑡)
𝑠,𝑡∈𝑆(𝑥,𝑦)
Works well for salt noise or Gaussian noise, but fails for pepper noise
• Order-Statistic Filter: These are the spatial filters whose response is
based on ordering (ranking) the values of the pixels contained in the
image area encompassed by the filter. The ranking result determines
the response of the filter.
• Median filter : Good for salt-and-pepper noise
• Max filter : Useful for finding the brightest points in an image
• Min filter 12

13. • Example
13
Original
Image
Image
Corrupted
by Gaussian
Noise
3x3
arithmetic
mean filter
3x3
geometric
mean filter

14. Order-Statistic Filters
• Median filter:
14
3x3
median
filter
2nd Pass
Image Corrupted
by Salt and
Pepper Noise
3rd Pass

15. Order-Statistic Filters
15
Max Filter Min Filter

16. Inverse Filtering
• The simplest approach to restoration is direct inverse filtering, where
we compute an estimate, 𝐹 𝑢, 𝑣 , of the transform of the original
image simply by dividing the transform of the degraded image, G(u, v),
by the degraded function:
𝐹 𝑢, 𝑣 =
𝐺(𝑢, 𝑣)
𝐻(𝑢, 𝑣)
Substituting the RHS of frequency domain representation of
the model of image degradation/reconstruction we get:
𝐹 𝑢, 𝑣 = 𝐹 𝑢, 𝑣 +
𝑁(𝑢, 𝑣)
𝐻(𝑢, 𝑣)
This equation tells that, even if we know the degradation function we
cannot recover the un-degraded image [F(u, v)] exactly because N(u, v) is
not known.
If degradation function has zero or very small value then the ratio could
easily dominate the result. 16

17. Minimum Mean Square Error
(Wiener) Filtering
• Inverse filtering approach has no provision for noise handling.
• This method is based on considering image and noise as
random variables, and objective is to find an estimate 𝑓of the
uncorrupted image 𝑓such that the mean square error
between them is minimized. The error measure is given by:
𝑒2 = 𝐸{ 𝑓 − 𝑓
2
}
where, 𝐸{. } is expected value of the argument.
Assumptions: i) Noise and image are uncorrelated;
ii) Any one has zero mean.
Based on these conditions, the minimum error function in above
equation is given in the frequency domain by:
17

18. Minimum Mean Square Error
(Wiener) Filtering
• Here, the fact that the product of a complex quantity with
conjugate is equal to the magnitude of the complex quantity
squared. This result is known as the Wiener filter.
18

19. • Mean Square Error
• Signal to Noise Ratio
19

20. Fourier Slice theorem
• Fourier slice theorem (FST) explains the reconstruction of the
object from the projection data.
• It is derived by taking the one dimension Fourier transform of
the parallel projections and noting that it is equal to the slices
of the two dimensions Fourier transform of the object
• The projection data should estimate the object using two
dimensional inverse Fourier transform
20

21. Fourier Slice theorem
• In above figure, the (x, y) coordinate system is rotated by an
angle θ.
• The FFT of the projection is equal to the 2-D FFT of the object
slice along a line rotated by θ.
• Thus the FST states that, the Fourier transform of parallel
projection of an image f(x, y) taken at an angle θ gives a slice
of the 2-D transform, subtending an angle θ with the u-axis.
• In other words one dimensional FT of the set of projections
gives the value of two dimensional FT along lines BB. 21

22. Fourier Slice theorem
22

23. Introduction
• Image reconstruction is simple and can be explained intuitively
considering an example.
a) Flat region with b) Result of
object, beam back projecting
& detector Sensed strip data
c) Beam & e) = b + d
detectors
rotated by 90˚
d) Back-projection
23

24. Introduction
• From (e) figure we can identify the object, whose amplitude is
twice that of individual back projection.
• As the number of projections increases, the strength of non-
intersecting back projections decreases relative to the
strength of regions in which multiple back projections
intersect.
• Net result: - Brighter region will dominate the result, and back
projections with few or no intersections will fade into the
background.
• Result from 32 back projections is shown next 24

25. Principles of Computed
Tomography (CT)
• In 1917, Johann Radon, a mathematician from Vienna derived
a method for projecting a 2-D object along parallel rays as part
of his work on line integrals.
• This method is known as Radon Transform.
• 45 years later, Allan Cormack, a physicist at Tufts University
rediscovered these concept and applied to CT.
• Godfrey N. Hounsfield & his colleagues at EMI in London built
first medical CT machine.
• Cormack & Hounsfield shared Noble Prize in 1979. 25

26. Principles of Computed
Tomography (CT)
• First Generation (G1) CT Scanners:
• It employ a pencil X-ray beam and a single detector.
26

27. Principles of Computed
Tomography (CT)
• Second Generation (G2) CT scanners
• Operates on same principle as G1 scanners, but the beam
used is in the shape of a fan.
27

28. Principles of Computed
Tomography (CT)
• Third Generation (G3) scanners
• They employ a bank of detectors long enough (around 1000) to
cover the entire field of view of a wider beam.
28

29. Principles of Computed
Tomography (CT)
• Fourth Generation (G4) scanners
• They employed a circular ring of detectors (around 5000), only
the source has to rotate.
29

30. 4 Generations
of CT Scanners
30

31. Principles of Computed
Tomography (CT)
• Fifth Generation (G5) CT scanners a.k.a. electron beam
computed tomography (EBCT) eliminate all mechanical motion
by employing electron beams controlled electromagnetically.
• Sixth Generation (G6) scanners a.k.a. helical CT. The
source/detector pairs rotates continuously through 360˚ while
the patient is moved at a constant speed along the axis
perpendicular to the scan.
• Seventh Generation (G7) scanners a.k.a. multislice CT Scanners
are emerging in which thick fan beams are used in conjunction
with parallel banks of detectors to collect volumetric CT data
simultaneously.
31

32. Projections and the Radon
Transform
• A straight line in cartesian coordinates can be described either
by its slope intercept form,
y = ax + b
Or
x cos θ + y sin θ = ρ
32

33. Projections and the Radon
Transform
• The projection of a parallel ray beam may be modeled by a set
of such lines as,
33

34. Projections and the Radon
Transform
• An arbitrary point in the projection signal is given by the raysum
along the line x cos θk + y sin θk = ρj
• The raysum is a line integral given by:
• If all the values of ρ & θ are considered the above equation
becomes
34

35. Projections and the Radon
Transform
• The equation in discrete form becomes
where, x, y, ρ & θ are discrete variables.
• When the Radon transform, g(ρ, θ), is displayed as an image with ρ
& θ as rectilinear coordinates, the result is called a sinogram (like
Fourier transform, however, g(ρ, θ) is always a real function.)
• Like Fourier Transform, a sinogram contains data necessary to
reconstruct f(x, y).
35

36. Projections and the Radon Transform
36

37. Projections and the Radon
Transform
• The key objective of CT is to obtain a 3D representation of a
volume from its projections.
• The approach is to back-project each projection and then sum
all the back projections to generate one image.
• Stacking all the resulting images produces a 3D rendition of
the volume.
• To obtain a formal expression for a back-projected image from
the Radon Transform, begin with a single point, g(ρi, θk) of the
complete projection, g(ρ, θk), for a fixed value of rotation, θk. 37

38. Projections and the Radon
Transform
• In general, the Image formed from a single back projection obtained
at an angle θ is given by:
• Final image is formed by integrating all back projected images
• In discrete case, the integral becomes sum of all back projected
images
where, x, y & θ are discrete variables.
38

39. Reconstruction using Parallel-
Beam Filtered Backprojections
39

40. Reconstruction using Parallel-
Beam Filtered Back projections
• Obtaining back projections yields blurred results.
• Straightforward solution to this problem is filtering the
projections before computing the back projections.
• Using 2-D Inverse Fourier Transform of F(u, v) is:
• Taking, u = ω cosθ & v = ω sinθ & dudv = ω dω dθ, we can
express above equation in polar coordinates: 40

41. Reconstruction using Parallel-
Beam Filtered Back projections
• Then, using Fourier-Slice theorem,
• Splitting the integral in 2 expressions, for θ in the range 0˚ to
180˚ & 180˚ to 360˚ and using the fact G(ω,θ + 180˚) = G(-ω,θ)
we get,
• In the term w.r.t. ω, the term x cos θ + y sin θ = ρ
41

42. Reconstruction using Parallel-
Beam Filtered Back projections
• The term inside the bracket is inverse Fourier Transform of the
product of two frequency domain functions, which are equal
to the convolution of the spatial representations of these 2
functions.
42

43. Numerical
1) Use Radon transform to obtain an analytical expression for
projection of circular object shown below:
𝑓 𝑥, 𝑦 =
𝐴 𝑥2 + 𝑦2 ≤ 𝑟2
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
where, A – constant & r – radius of the object
Sol: We assume that, circle is centered on the
Origin of the xy-plane.
Since, the object is circularly symmetric, its
projections are the same for all angles.
So, we have to obtain the projection for θ = 0˚
43

44. Numerical
The equation for Radon transform is given as:
𝑔 ρ, θ = 𝑓 𝑥, 𝑦 δ 𝑥 − ρ 𝑑𝑥 𝑑𝑦
∞
−∞
∞
−∞
= 𝑓 ρ, 𝑦 𝑑𝑦
∞
−∞
This is a line integral along the line L(ρ, 0) in this case.
Here, 𝑔 ρ, θ = 0 when ρ > r.
When ρ ≤ r ; integral is evaluated from y= − 𝑟2 − ρ2 to y=
𝑟2 − ρ2
So, 𝑔 ρ, θ = 𝑓 ρ, 𝑦 𝑑𝑦
𝑟2−ρ2
− 𝑟2−ρ2
= 𝐴 𝑑𝑦
𝑟2−ρ2
− 𝑟2−ρ2
44

45. Numerical
Integrating results in,
𝑔 ρ, θ = 𝑔 ρ = 2𝐴 𝑟2 − ρ2 ρ ≤ r
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
Here, we used the fact that,
𝑔 ρ, θ = 0 when ρ > r.
Note that, 𝑔 ρ, θ = 𝑔 ρ ;
that is, g is independent of θ
because the object is symmetric
about the origin.
45