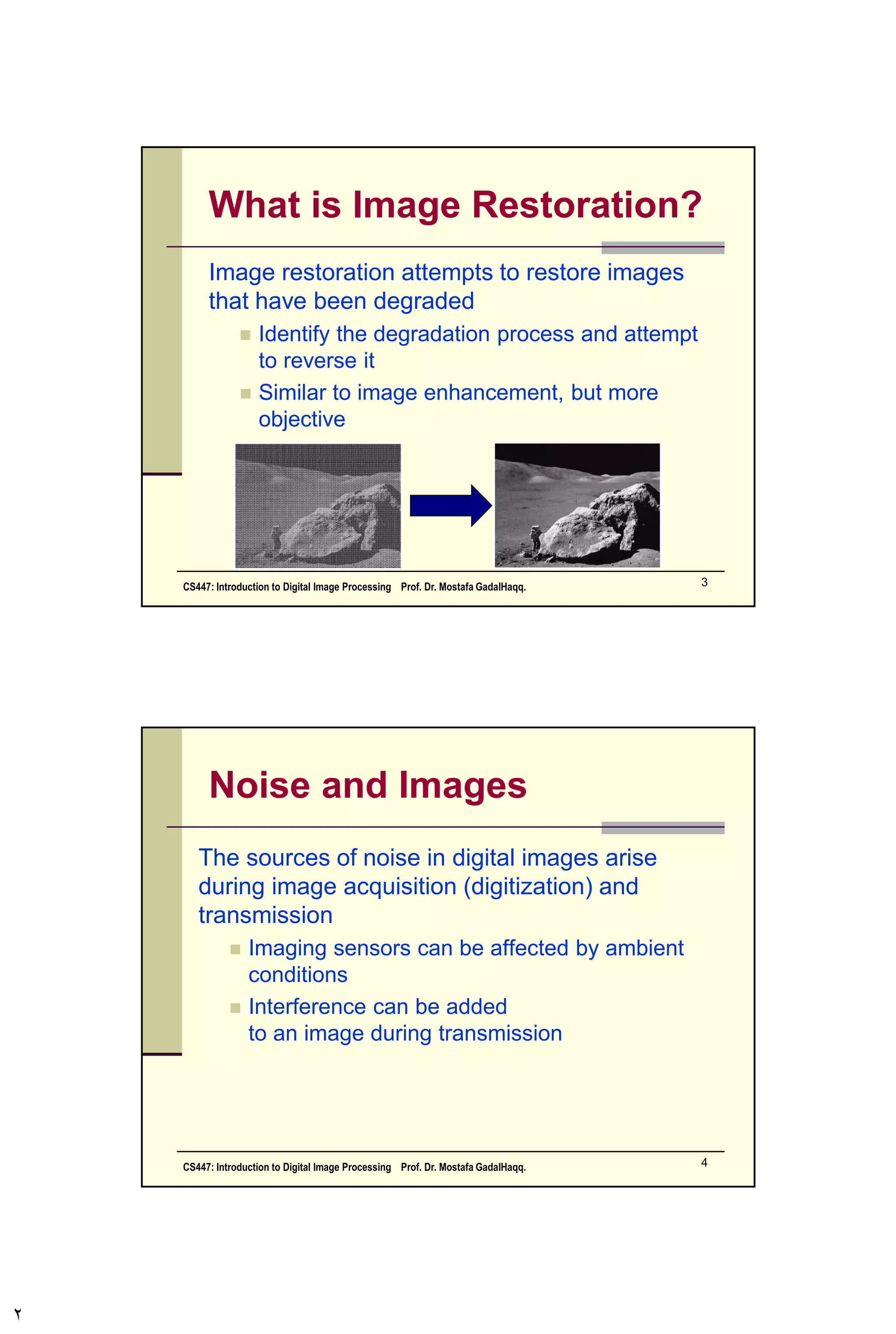
This document discusses image restoration techniques for noise removal, including:
- Spatial domain filtering techniques like mean, median, and order statistics filters to remove random noise.
- Frequency domain filtering like band reject filters to remove periodic noise.
- Adaptive filtering techniques where the filter size changes depending on image characteristics within the filter region to better handle impulse noise.