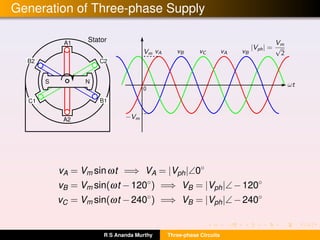
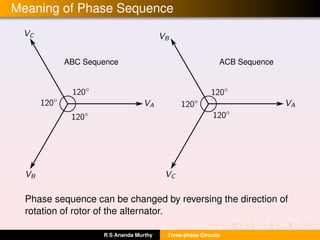
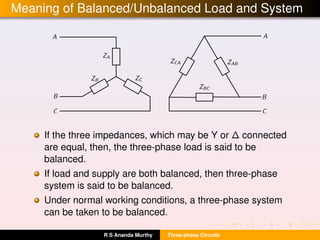
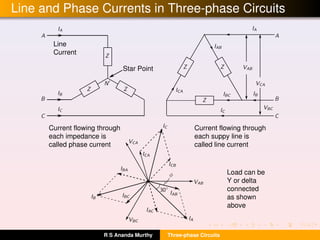
The document discusses three-phase circuits and provides information on: - The advantages of three-phase supply systems such as higher efficiency of power transfer and smoother load characteristics. - Key concepts like phase sequence, balanced/unbalanced supply and load, and the relationships between line and phase voltages and currents. - How to calculate power in a balanced three-phase system and use two wattmeters to measure total power and power factor.

1. Three-phase Circuits
Workshop on Basic Electrical Engineering held at
VVCE, Mysuru, on 30-April-2016
R S Ananda Murthy
Associate Professor
Department of Electrical & Electronics Engineering,
Sri Jayachamarajendra College of Engineering,
Mysore 570 006
R S Ananda Murthy Three-phase Circuits

2. Learning Outcomes
After completing this lecture the student should be able to –
State the advantages of three-phase supply.
State the meaning of phase sequence, balanced supply,
balanced load, and balanced system.
Derive the relationship between line and phase values of
voltages and currents in a balanced system.
Derive equation for the power consumed by a three-phase
balanced load.
Show that power in a three-phase three-wire system can
be measured using two wattmeters.
Find the power factor of a balanced three-phase load using
two wattmeter readings.
R S Ananda Murthy Three-phase Circuits

3. Advantages of Three-phase Supply
The amount of conducting material required to transfer a
given amount of power is minimum in a three-phase
system.
The instantaneous power in a three-phase system never
falls to zero resulting in smoother and better operating
characteristics of the load.
Three-phase supply is required by three-phase induction
motors which are widely used in industry because of their
ruggedness, longer life, higher torque, low initial and
maintenance costs.
R S Ananda Murthy Three-phase Circuits

4. Advantages of Three-phase Supply
Domestic as well as industrial and commercial power can
be supplied from the same three-phase distribution system.
Three-phase system has better voltage regulation.
For a given size of the machine, the power generated by a
three-phase alternator is higher.
R S Ananda Murthy Three-phase Circuits

5. Generation of Three-phase Supply
NS
A1
A2
C2
Stator
C1 B1
B2
vA = Vm sinωt =⇒ VA = |Vph|∠0◦
vB = Vm sin(ωt −120◦
) =⇒ VB = |Vph|∠−120◦
vC = Vm sin(ωt −240◦
) =⇒ VB = |Vph|∠−240◦
R S Ananda Murthy Three-phase Circuits

6. Meaning of Phase Sequence
ABC Sequence ACB Sequence
Phase sequence can be changed by reversing the direction of
rotation of rotor of the alternator.
R S Ananda Murthy Three-phase Circuits

7. Meaning of Balanced and Unbalanced Supply
(a) (b) (c) (d)
If |VA| = |VB| = |VC| = |Vph| and if the phase difference
between VA and VB, VB and VC, VC and VA is equal to
120◦ as shown in (a) then, the supply is said to be
balanced or symmetrical.
Phasor diagrams (b), (c), and (d) represent unbalanced
supply. Can you explain why?
R S Ananda Murthy Three-phase Circuits

8. Meaning of Balanced/Unbalanced Load and System
If the three impedances, which may be Y or ∆ connected
are equal, then, the three-phase load is said to be
balanced.
If load and supply are both balanced, then three-phase
system is said to be balanced.
Under normal working conditions, a three-phase system
can be taken to be balanced.
R S Ananda Murthy Three-phase Circuits

9. Relation between Line and Phase Voltages
ABC Sequence
If supply is balanced, then, line voltage magnitudes will be
|VAB| = |VBC| = |VCA| =
√
3|Vph| = |V|.
When phase sequence is ABC, VAB leads VAN by 30◦, VBC
leads VBN by 30◦, and VCA leads VCN by 30◦.
R S Ananda Murthy Three-phase Circuits

10. Relation between Line and Phase Voltages
If supply is balanced, then, line voltage magnitudes will be
|VAB| = |VBC| = |VCA| =
√
3|Vph| = |V|.
When phase sequence is ACB, VAB lags VAN by 30◦, VBC
lags VBN by 30◦, and VCA lags VCN by 30◦.
R S Ananda Murthy Three-phase Circuits

11. Line and Phase Currents in Three-phase Circuits
Star Point
Line
Current
Current flowing through
each impedance is
called phase current
Current flowing through
each suppy line is
called line current
Load can be
Y or delta
connected
as shown
above
R S Ananda Murthy Three-phase Circuits

12. Relation between Line and Phase Currents
In Y-connected load, the line current is equal to the phase
current.
From the phasor diagram given in the previous slide, it is
clear that
|IA| = 2|IAB|cos30◦
=
√
3·|IAB| =
√
3·
|V|
|Z|
= |IB| = |IC| = |I|
i.e., in a balanced ∆-connected three-phase load, the line
current is
√
3×|Iph| where |Iph| = |V|/|Z|.
R S Ananda Murthy Three-phase Circuits

13. Zero Neutral Shift Voltage in Balanced System
A
C B
Balanced Supply Balanced Load
Neutral Shift
Voltage
It can be shown that in a balanced system the neutral shift
voltage is zero so that VAN = VAN , VBN = VBN , and
VCN = VCN .
R S Ananda Murthy Three-phase Circuits

14. Power in Balanced System
A
B
C
Balanced
Three-phase
Supply
Total power consumed by the load is
P = 3Pph = 3|Vph|·|Iph|cosφ =
√
3·
√
3|Vph|·|Iph|cosφ
But
√
3|Vph| = |V| and |Iph| = |I| in a Y-connected load and
∆-connected load can always be replaced by equivalent Y. So,
P =
√
3·|V|·|I|·cosφ
R S Ananda Murthy Three-phase Circuits

15. Two Wattmeter Method to Measure 3-phase Power
M L
M L
COM
COM
V
V
Y or Delta
Connected
Three-phase
Balanced
Load
A
B
C
N
Balanced Supply
Wattmeter has current coil with terminals marked as M and L,
and voltage coil terminals marked as COM and V.
R S Ananda Murthy Three-phase Circuits

16. Two Wattmeter Method to Measure 3-phase Power
R S Ananda Murthy Three-phase Circuits

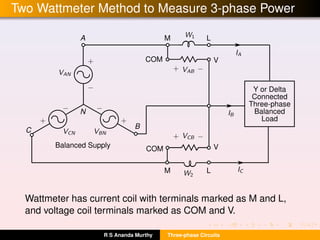
17. Two Wattmeter Method to Measure 3-phase Power
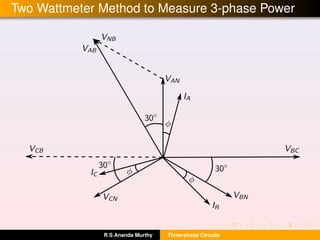
The reading of wattmeter W1 is given by
P1 = |VAB|×|IA|×cos(φ +30◦
) = |V||I|cos(30◦
+φ) (1)
where |V| and |I| are the line voltage and current respectively.
The reading of wattmeter W2 is
P2 = |VCB|×|IC|×cos(30◦
−φ) = |V||I|cos(30◦
−φ) (2)
So, the sum of the two wattmeter readings is
P1 +P2 = |V|·|I|·[cos(30◦
+φ)+cos(30◦
−φ)]
= 2|V|·|I|·cos30◦
cosφ
=
√
3|V|·|I|·cosφ (3)
which is nothing but the total three-phase active power.
R S Ananda Murthy Three-phase Circuits

18. Finding Power Factor from Two Wattmeter Readings
We can also write
P1 −P2 = |V|·|I|·[cos(30◦
+φ)−cos(30◦
−φ)]
= −2|V|·|I|·sin30◦
sinφ
= −|V|·|I|·sinφ (4)
Dividing Eq.(4) by Eq. (3) we get
P1 −P2
P1 +P2
=
−tanφ
√
3
=⇒ φ = tan−1
√
3(P2 −P1)
P1 +P2
(5)
from this the load power factor cosφ of the load can be found.
But the above equation can be applied only to balanced load.
R S Ananda Murthy Three-phase Circuits

19. License
This work is licensed under a
Creative Commons Attribution 4.0 International License.
R S Ananda Murthy Three-phase Circuits