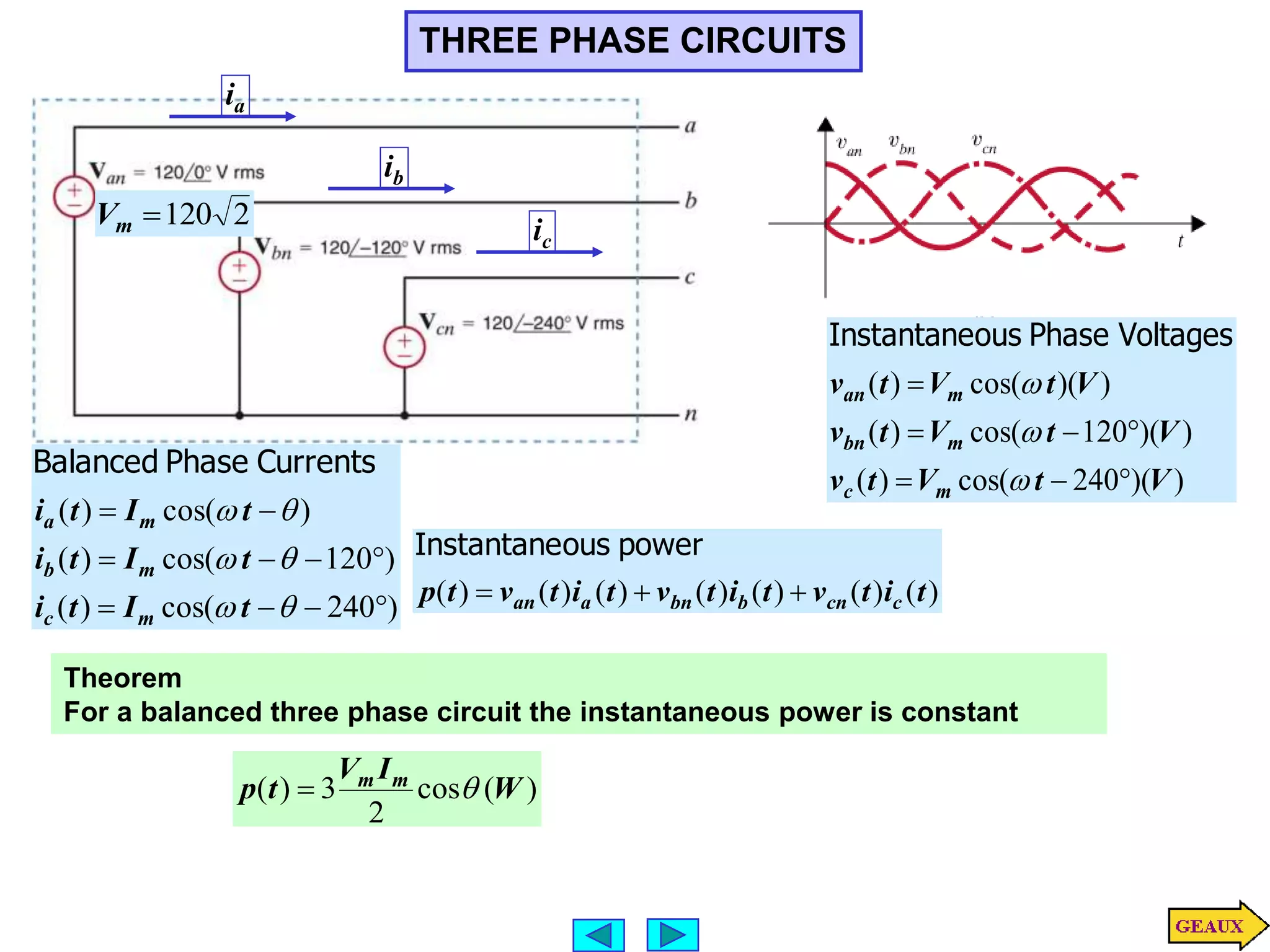
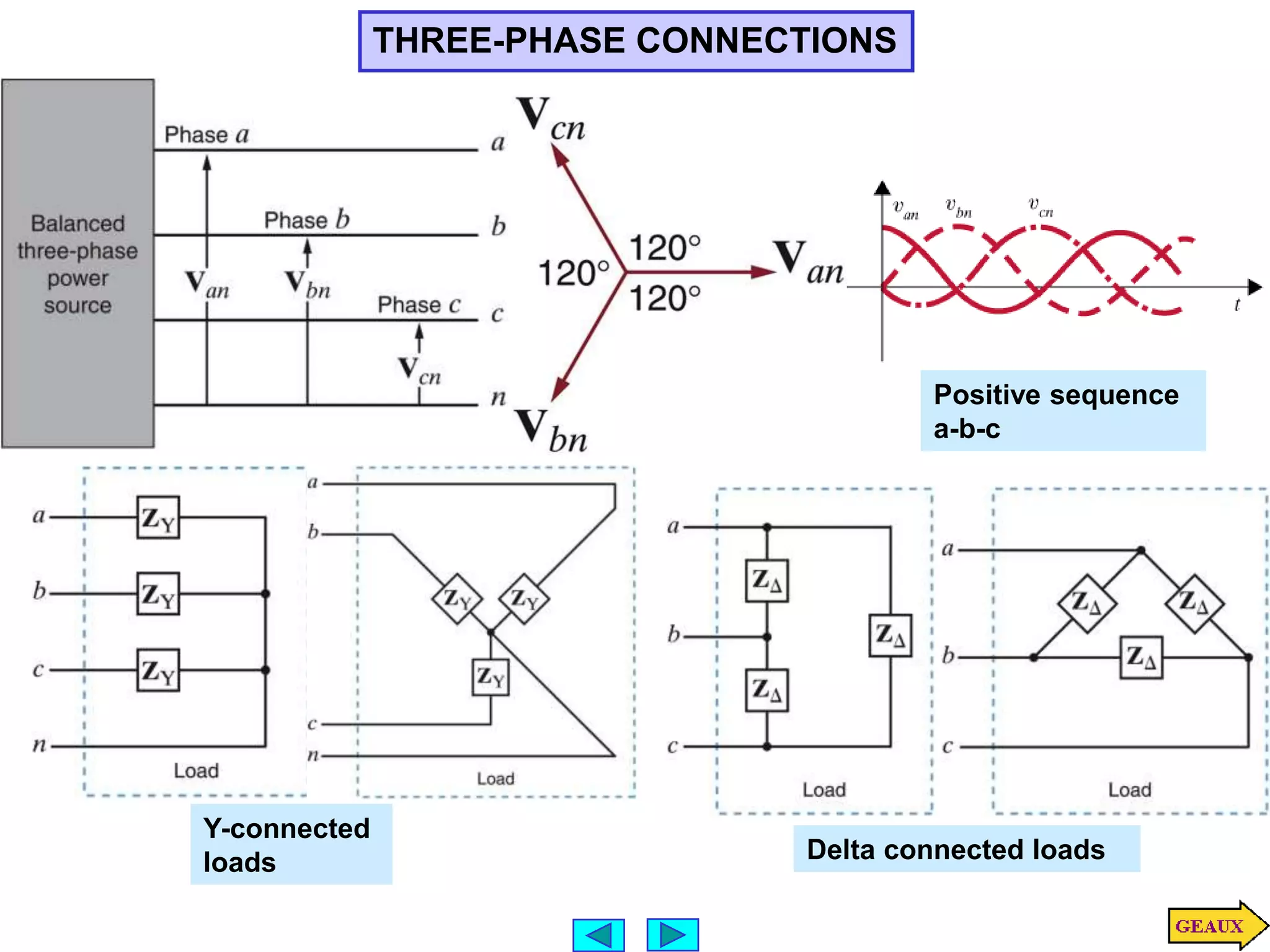
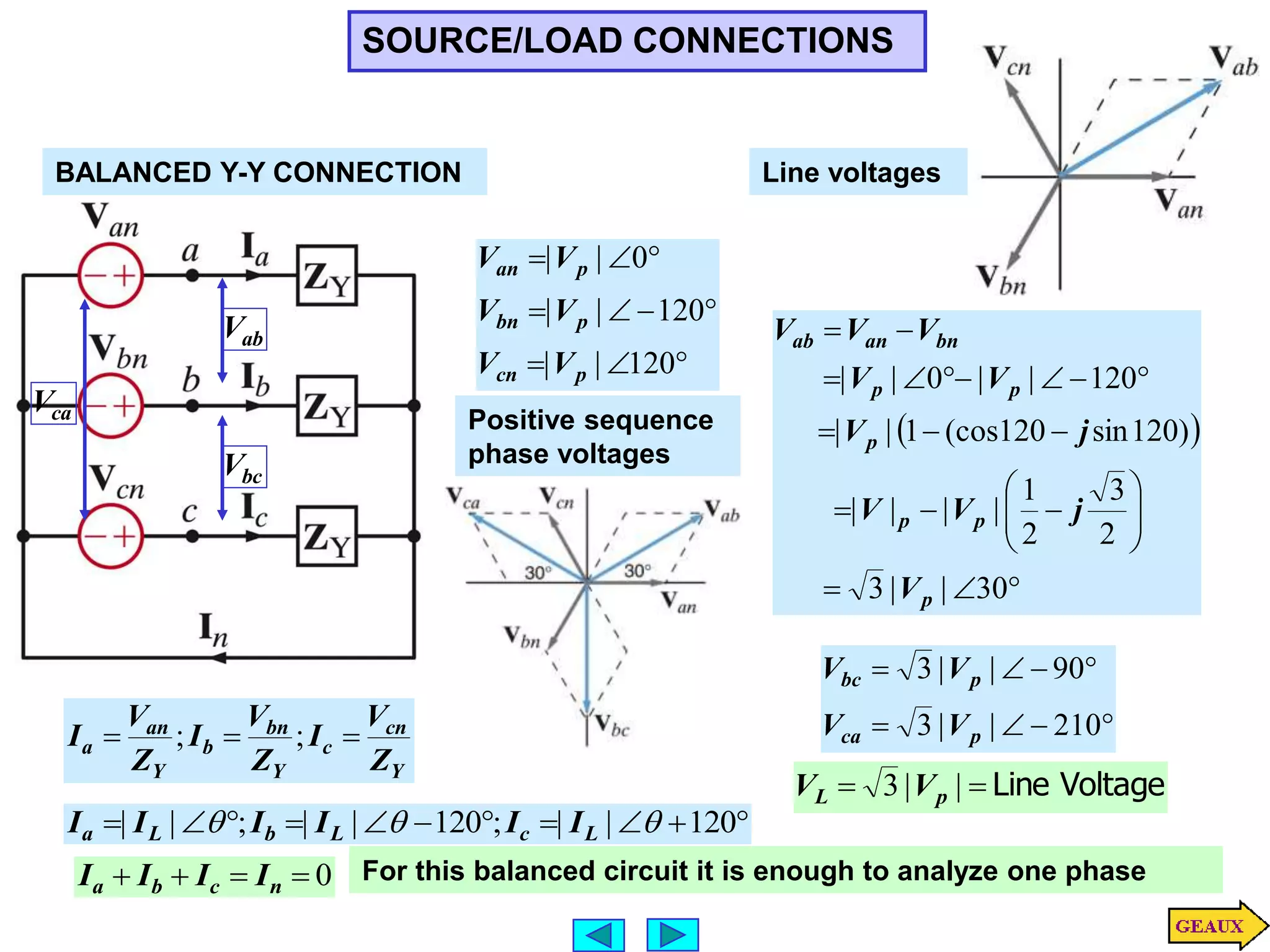
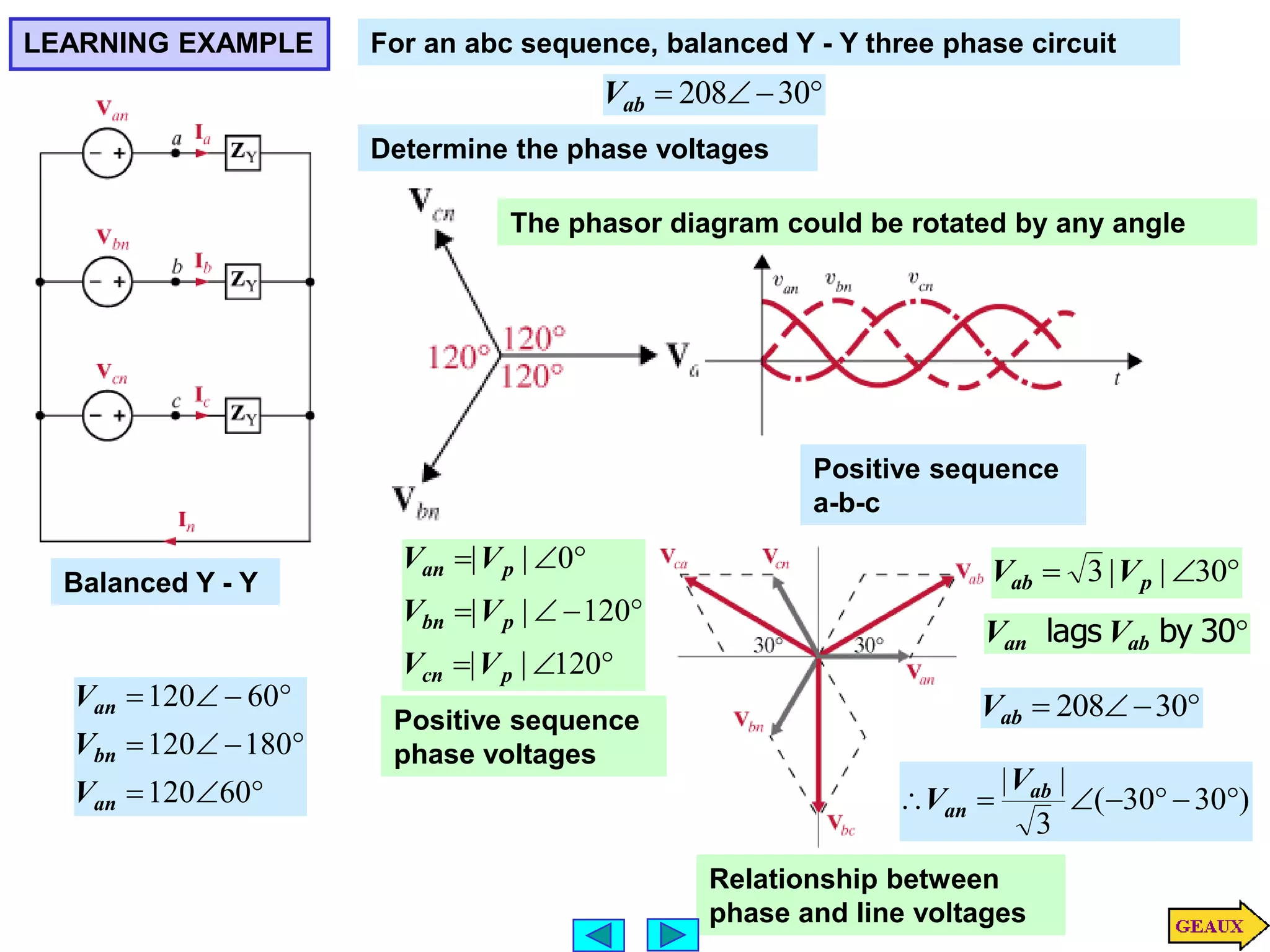
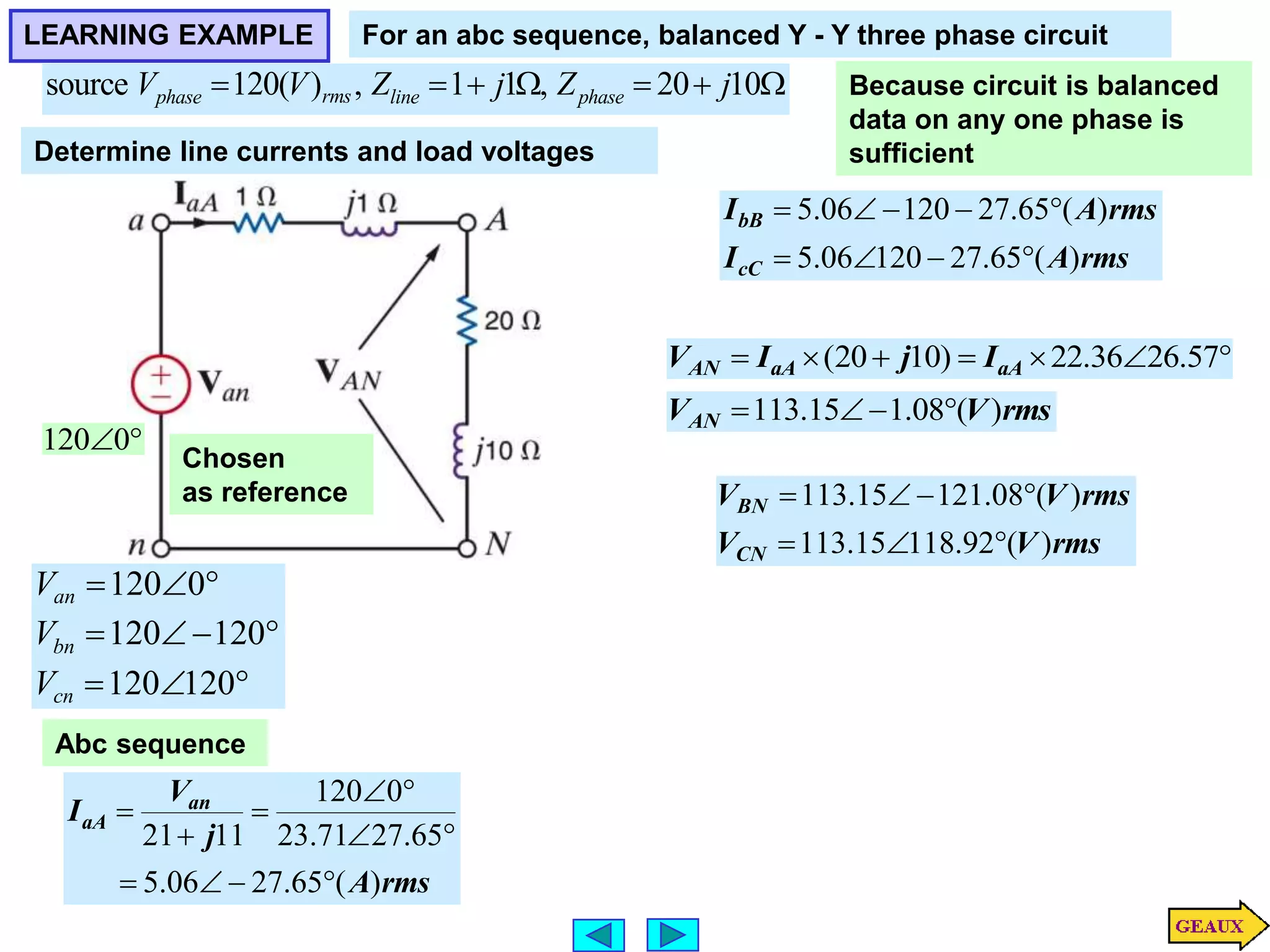
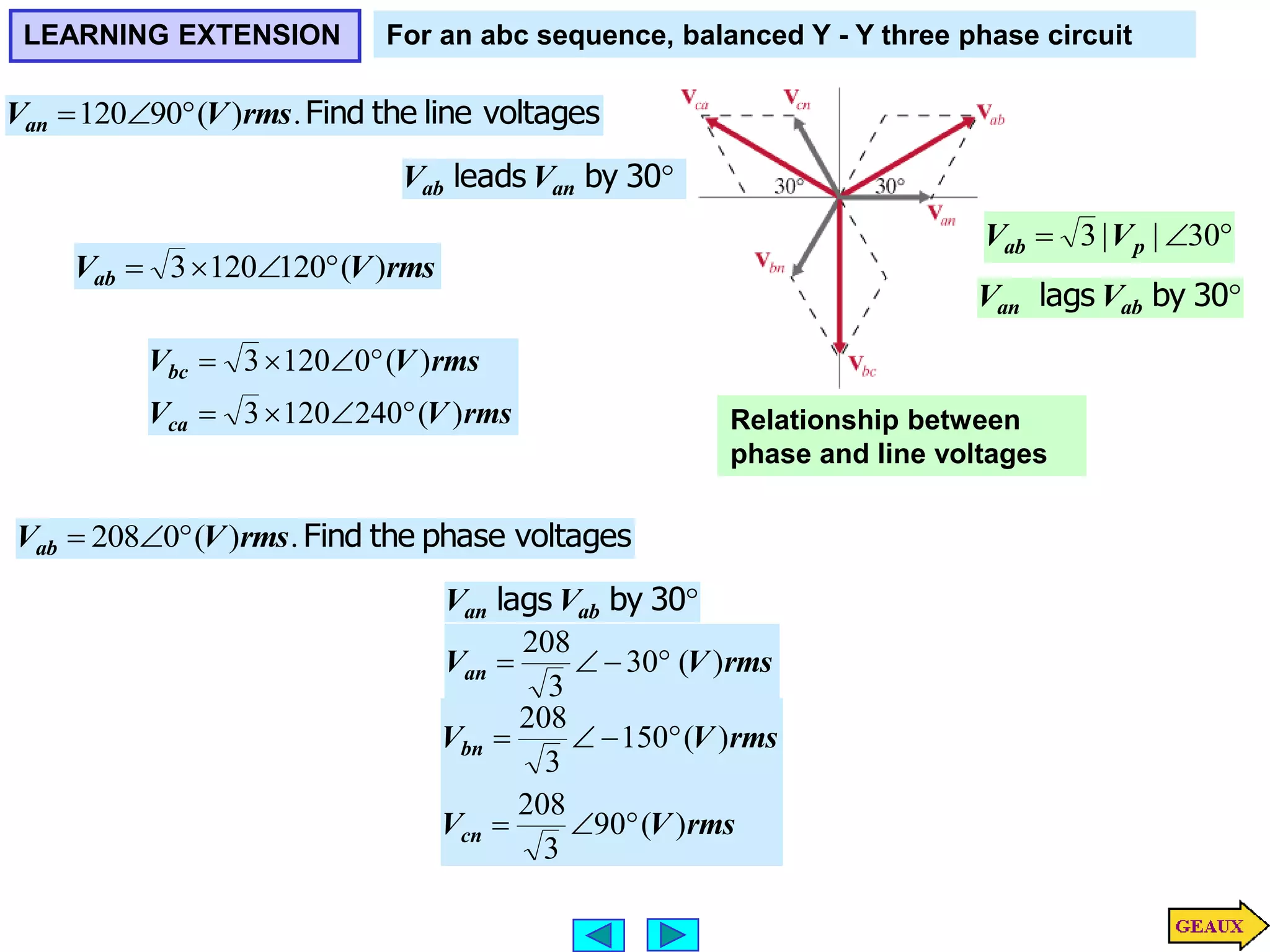
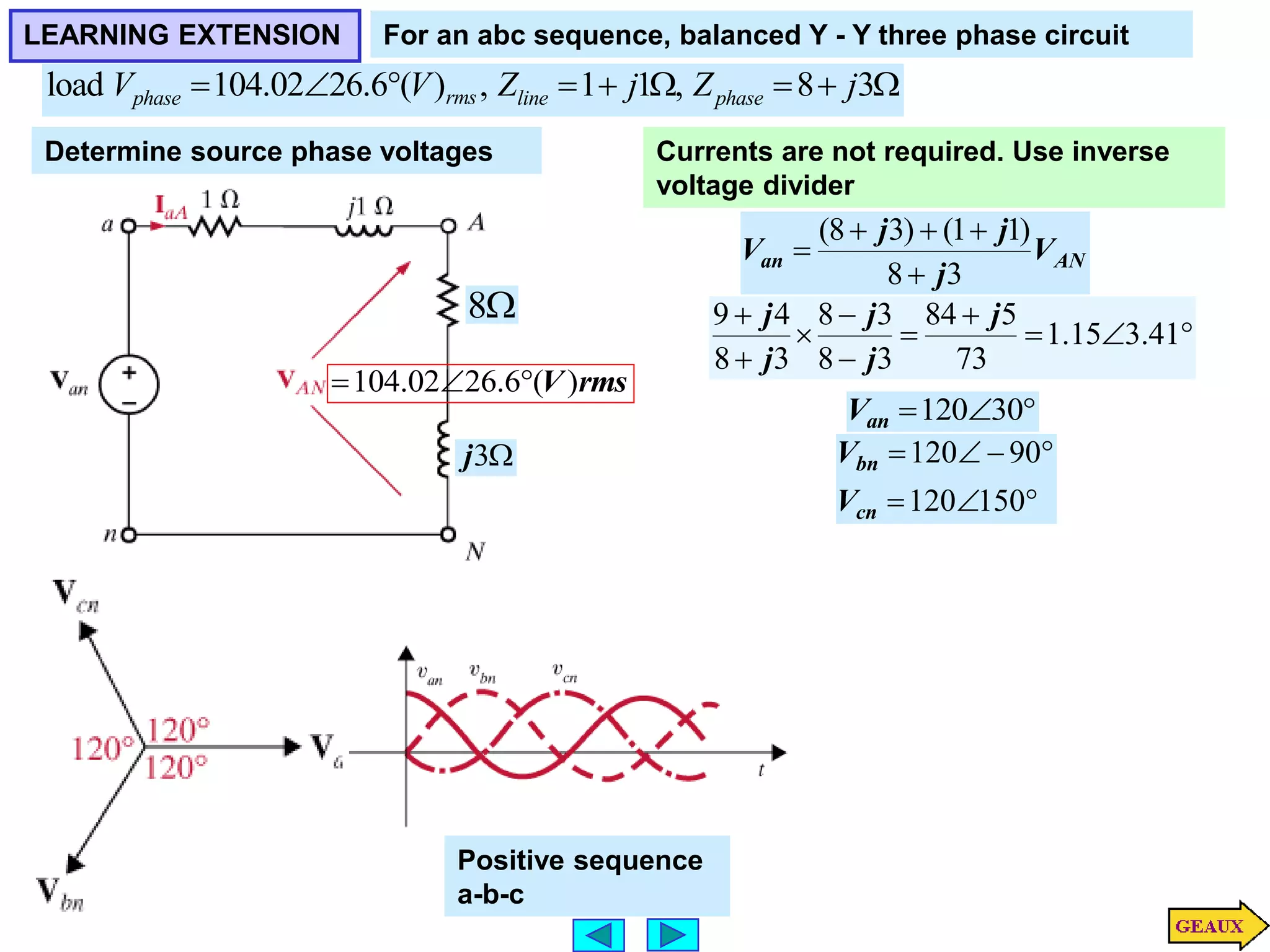
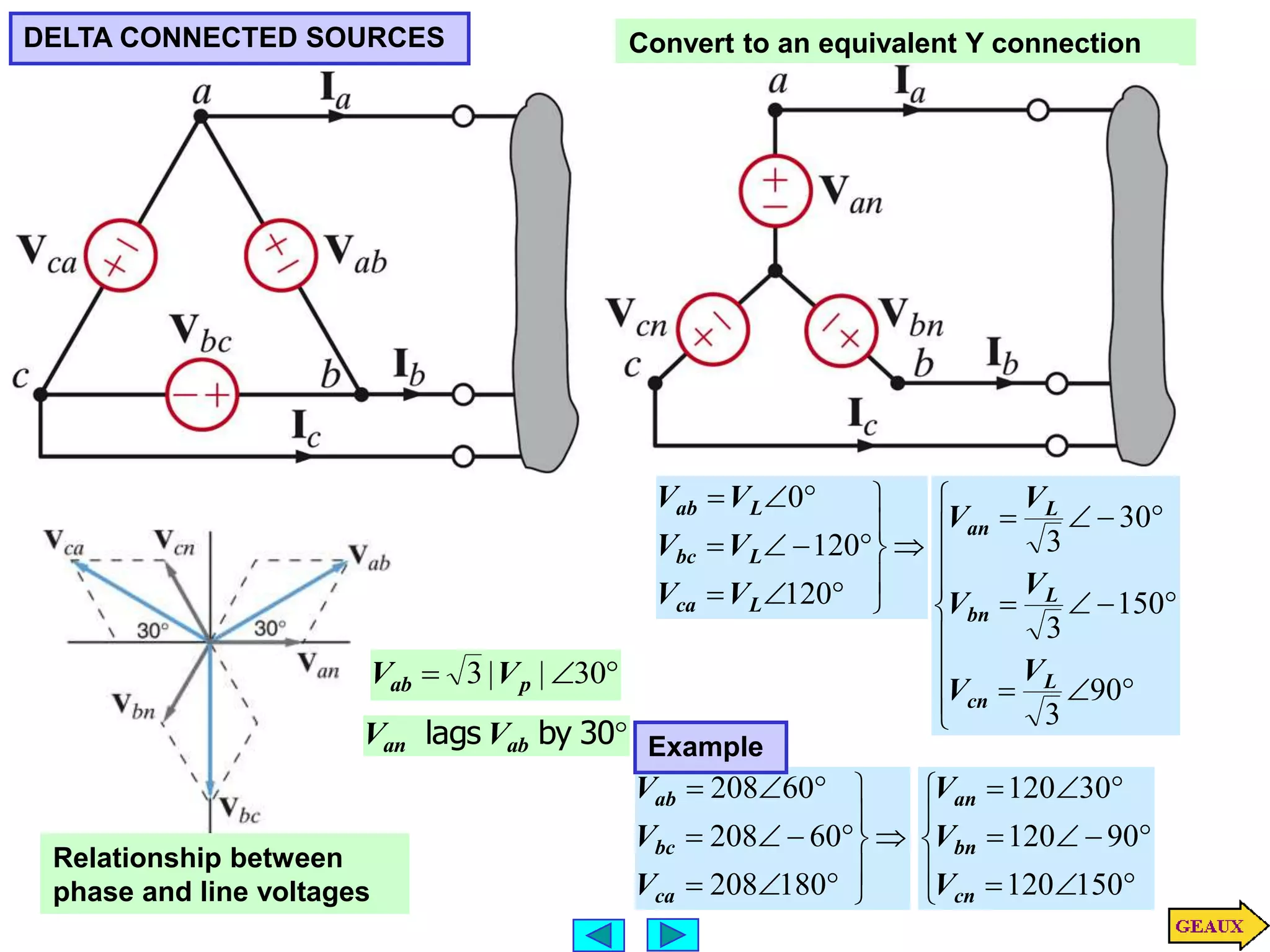
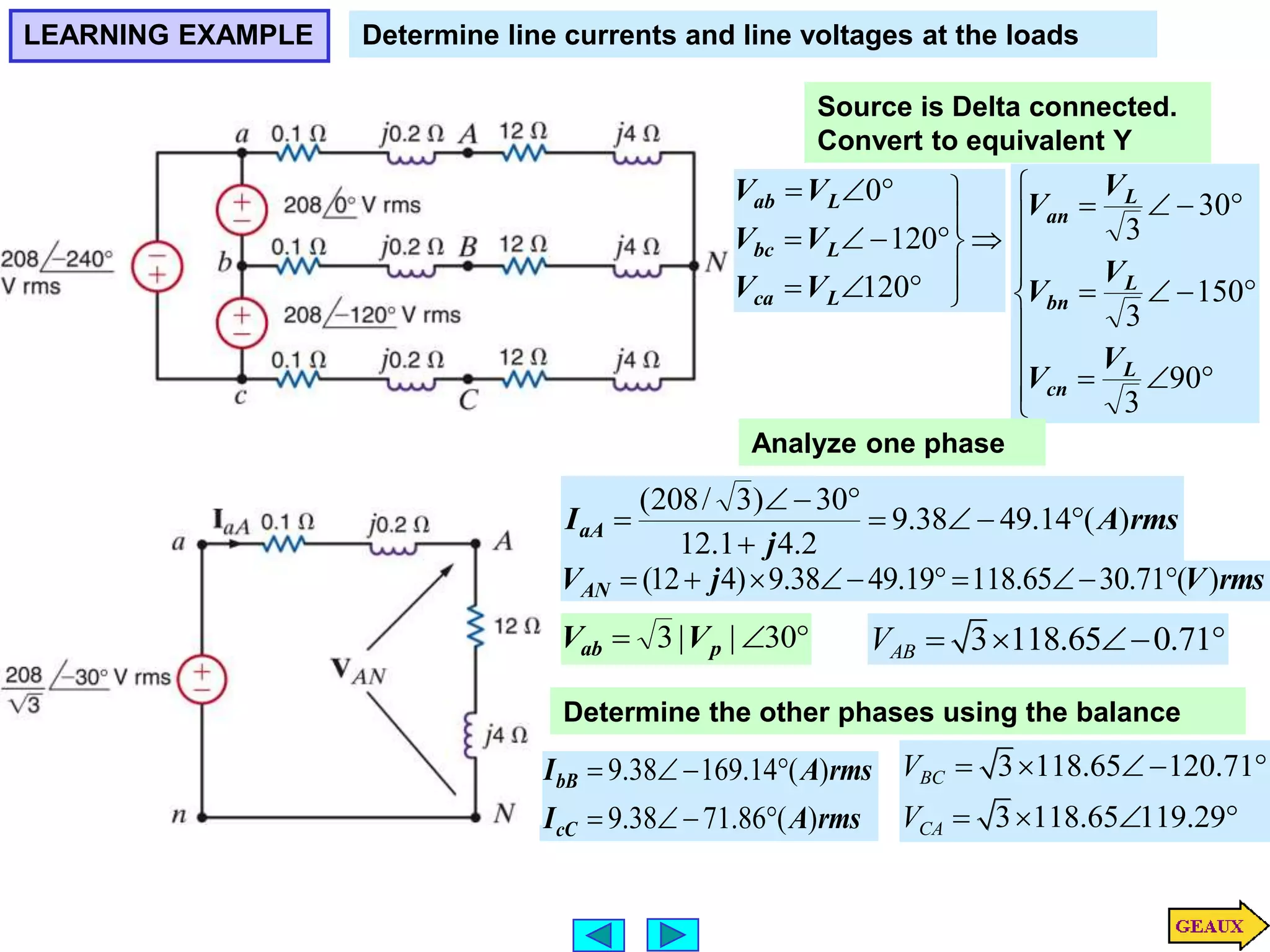
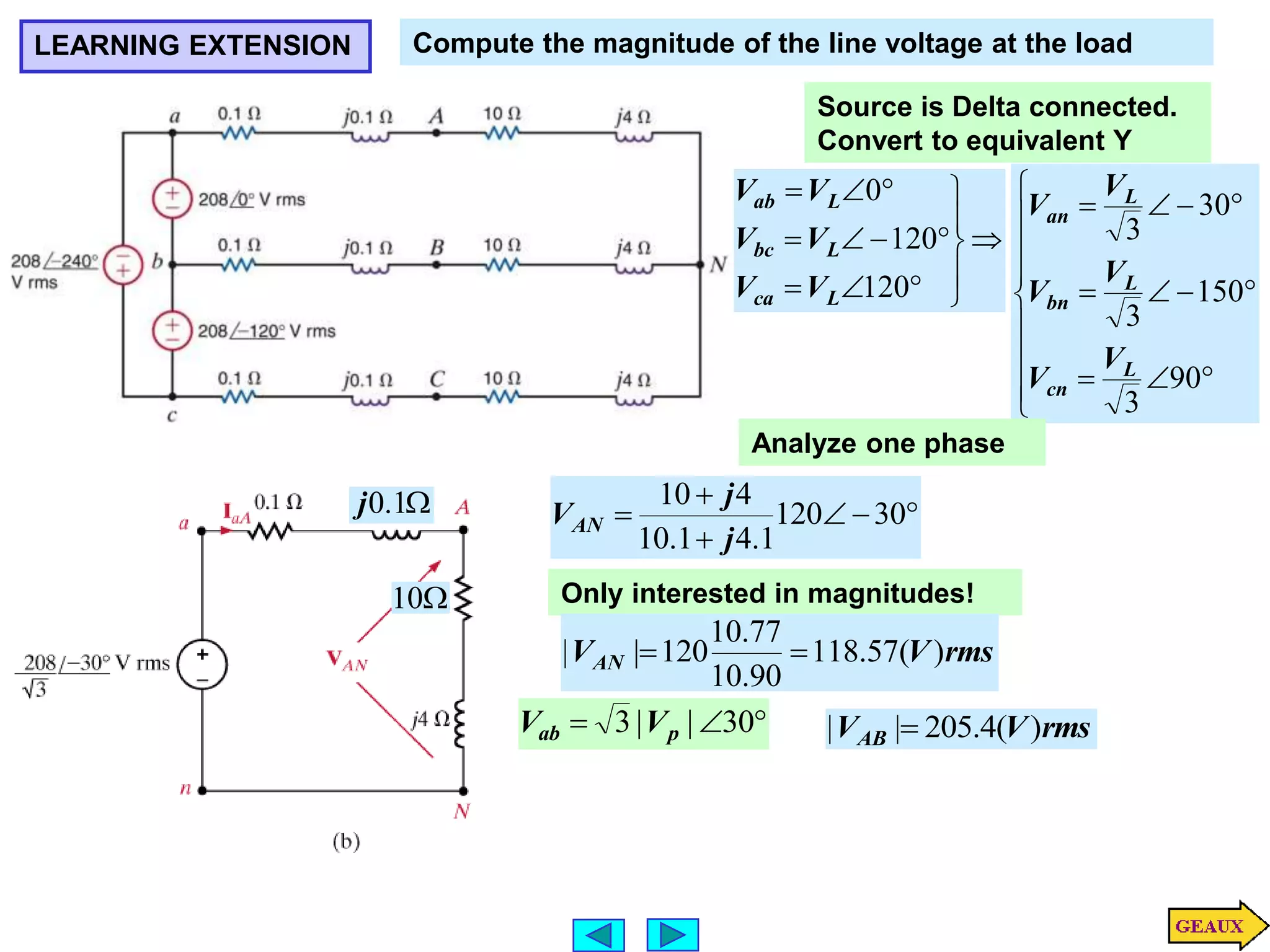
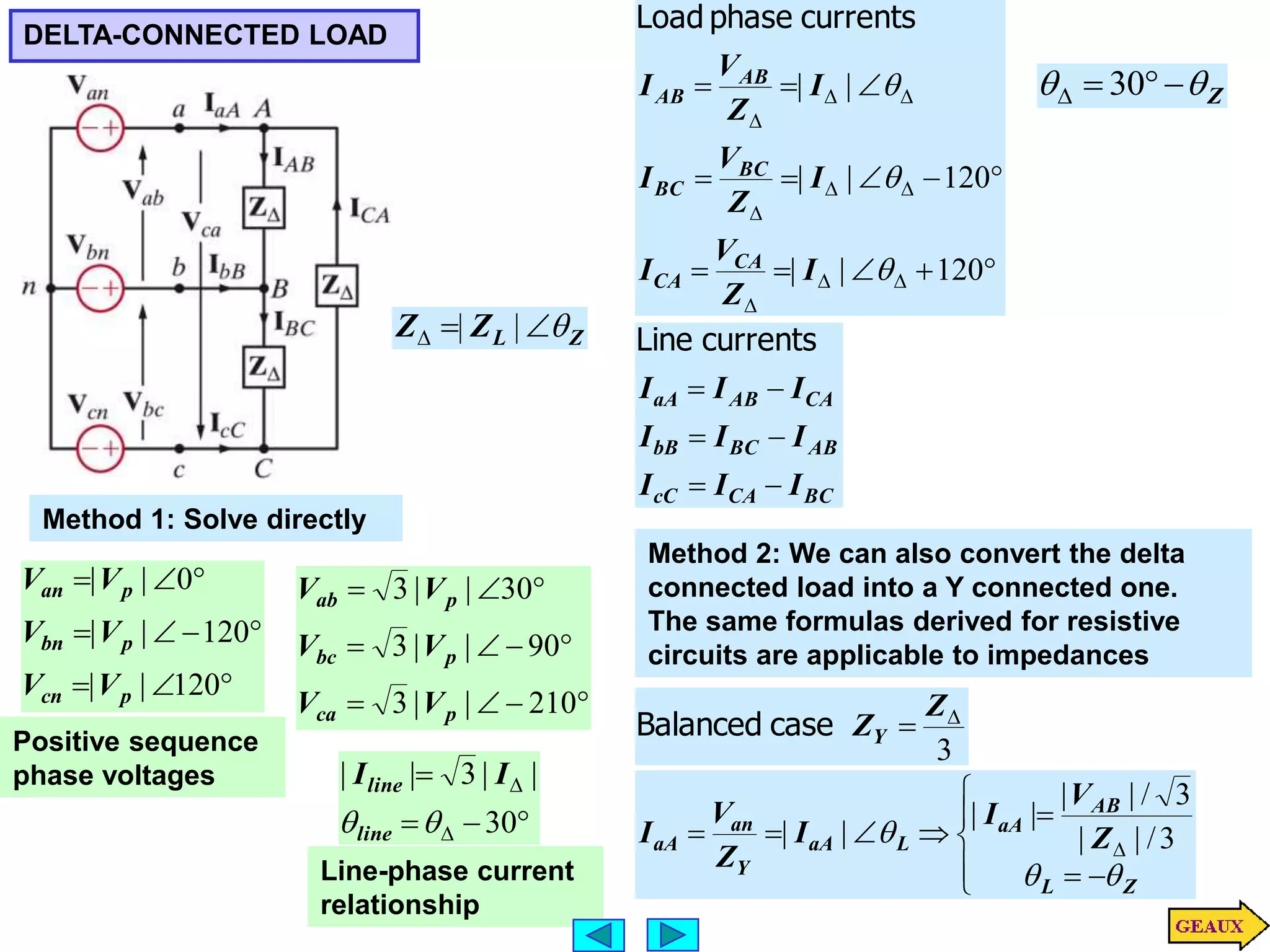
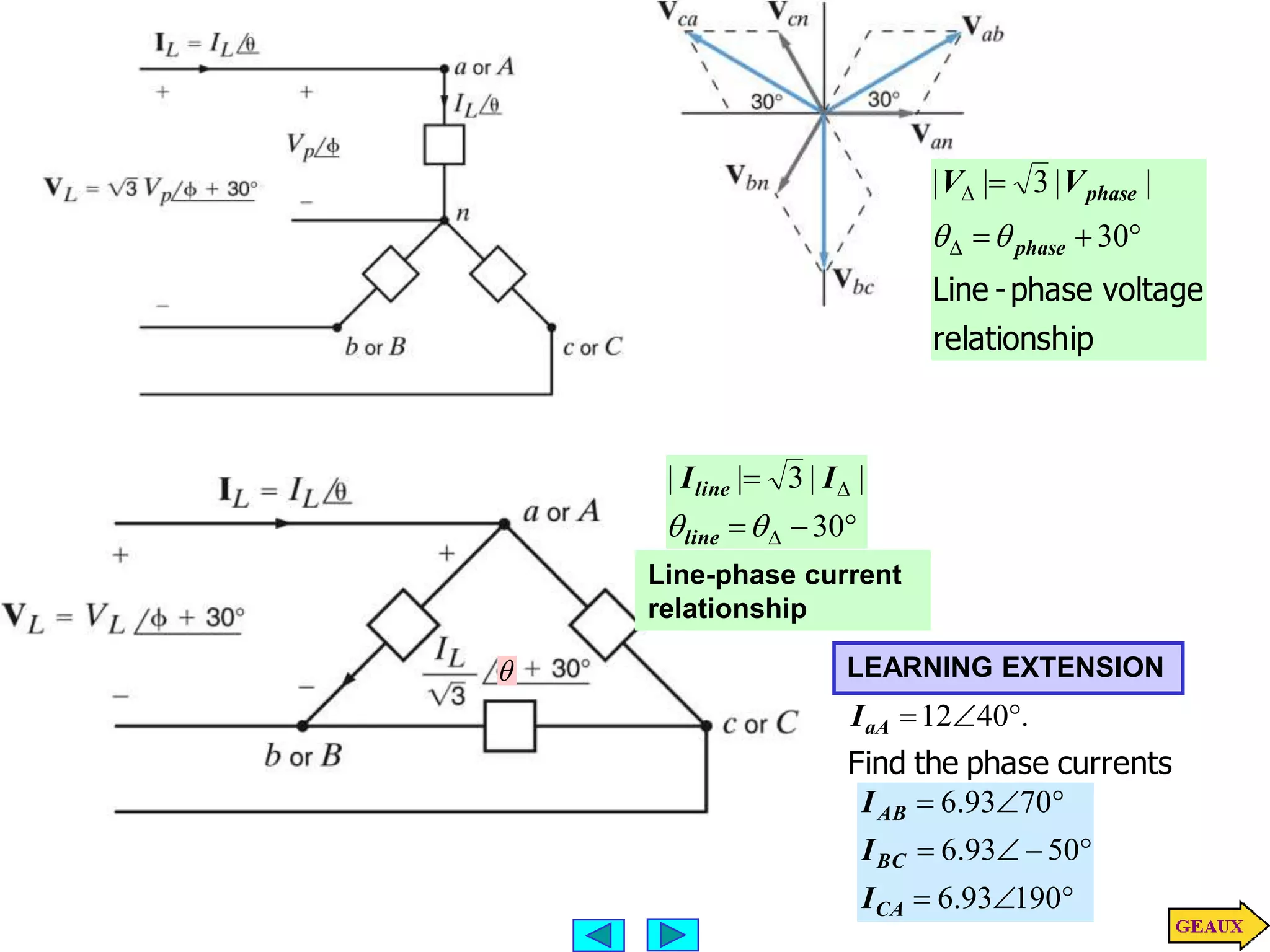
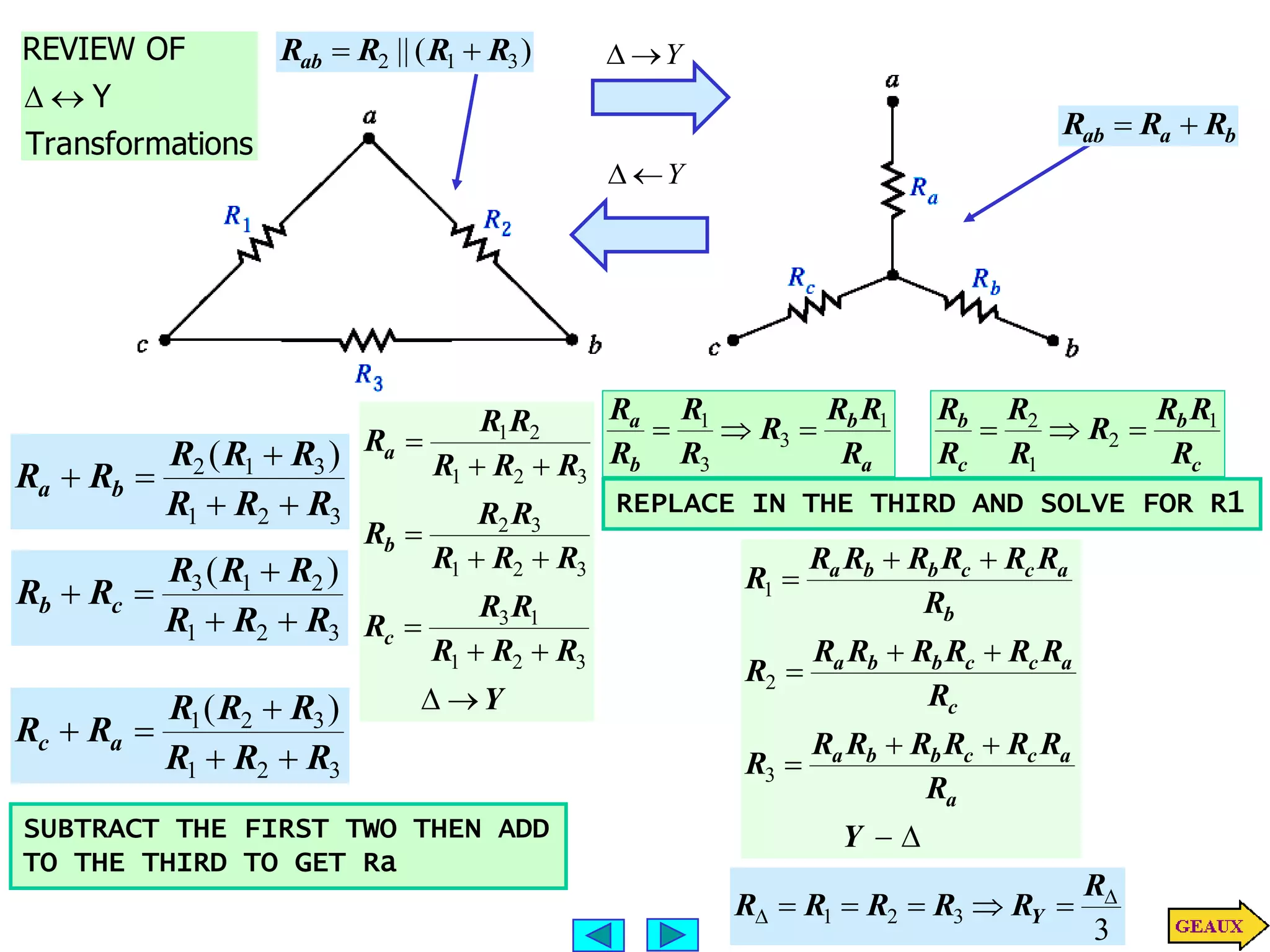
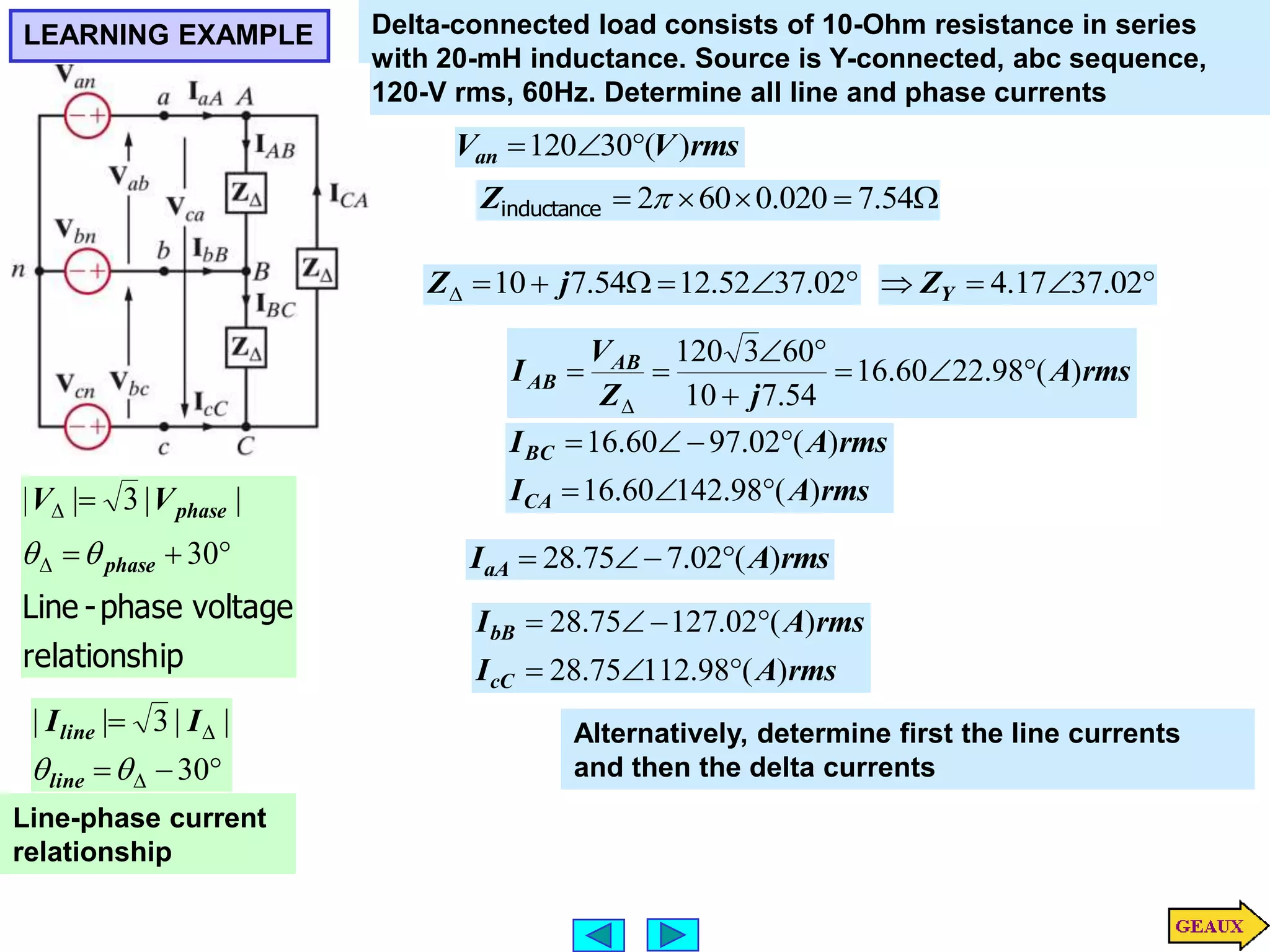
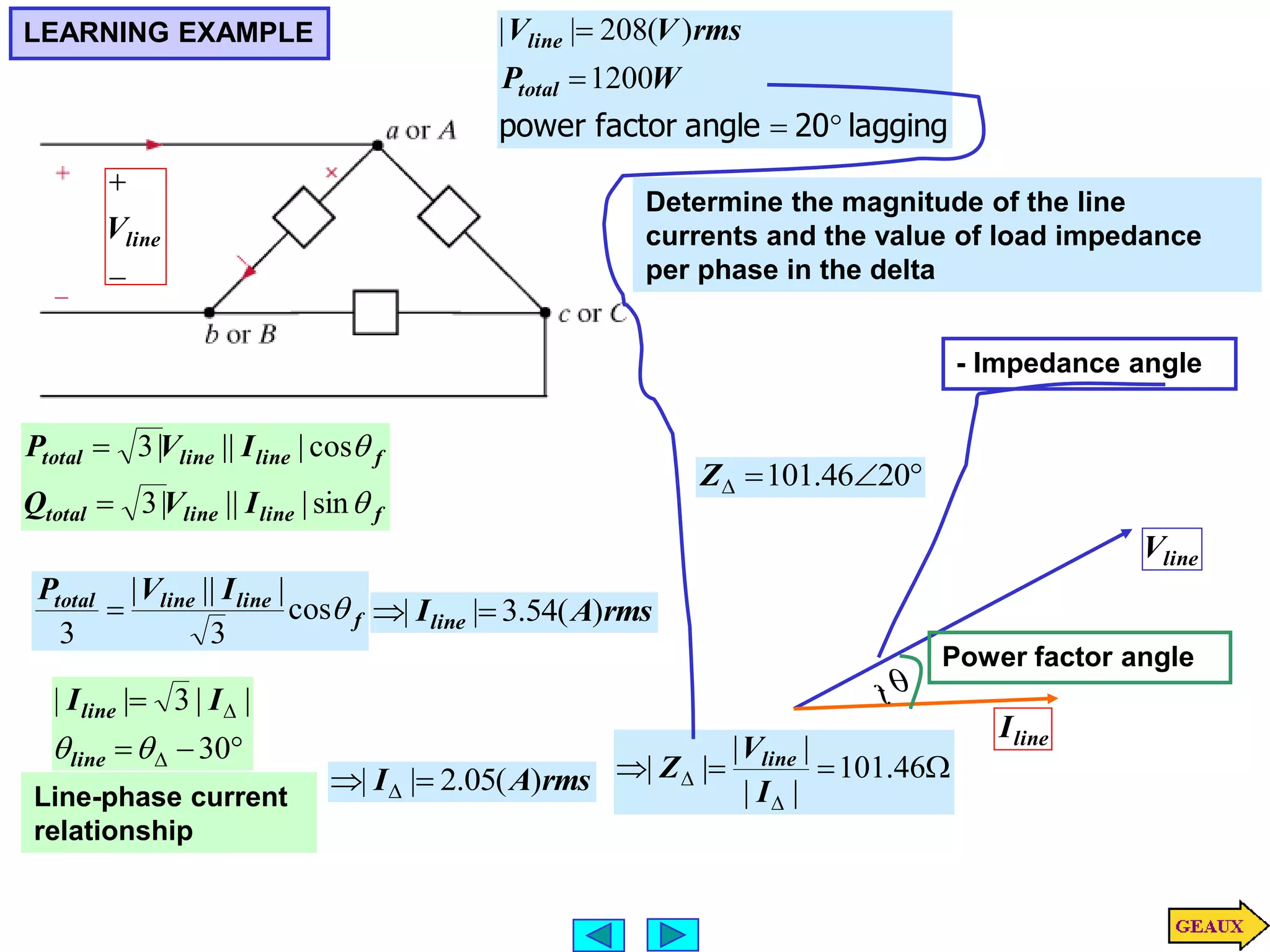
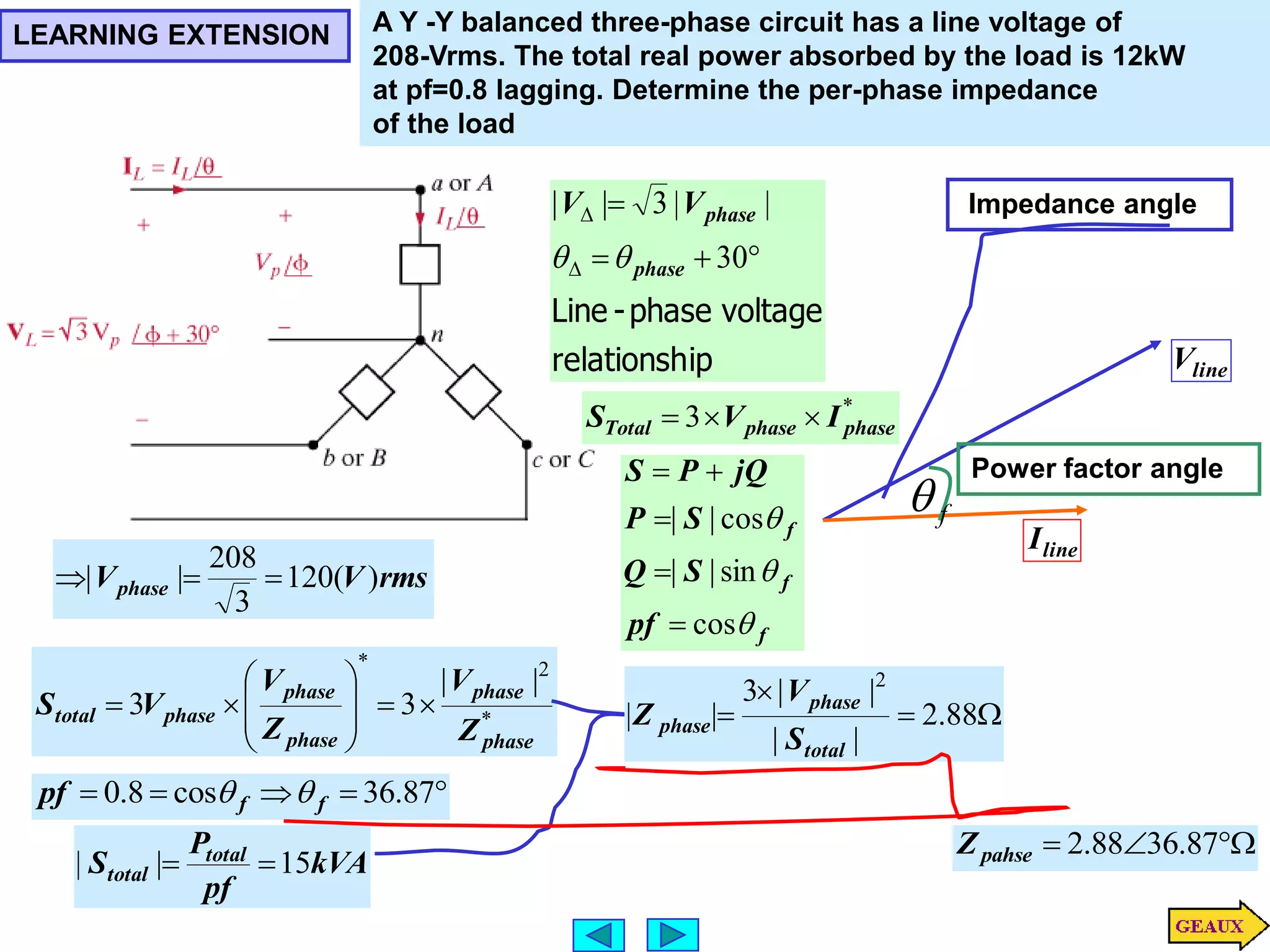
This document discusses three phase circuits. It covers the advantages of polyphase circuits, basic configurations including delta-wye connections, and power relationships in three phase circuits. Key concepts covered include instantaneous power in balanced three phase circuits remaining constant, voltage and current relationships in wye-wye and delta connections, and how to determine line currents and voltages from given phase information. Examples are provided to demonstrate calculating values for various three phase circuit connections.

1. POLYPHASE CIRCUITS
LEARNING GOALS
Three Phase Circuits
Advantages of polyphase circuits
Three Phase Connections
Basic configurations for three phase circuits
Source/Load Connections
Delta-Wye connections
Power Relationships
Study power delivered by three phase circuits

2. THREE PHASE CIRCUITS
)
)(
240
cos(
)
(
)
)(
120
cos(
)
(
)
)(
cos(
)
(
V
t
V
t
v
V
t
V
t
v
V
t
V
t
v
m
c
m
bn
m
an










Voltages
Phase
ous
Instantane
a
i
b
i
c
i
)
240
cos(
)
(
)
120
cos(
)
(
)
cos(
)
(
















t
I
t
i
t
I
t
i
t
I
t
i
m
c
m
b
m
a
Currents
Phase
Balanced
2
120

m
V
)
(
)
(
)
(
)
(
)
(
)
(
)
( t
i
t
v
t
i
t
v
t
i
t
v
t
p c
cn
b
bn
a
an 


power
ous
Instantane
Theorem
For a balanced three phase circuit the instantaneous power is constant
)
(
cos
2
3
)
( W
I
V
t
p m
m



3. Proof of Theorem
For a balanced three phase circuit the instantaneous power is constant
)
(
cos
2
3
)
( W
I
V
t
p m
m

























)
240
cos(
)
240
cos(
)
120
cos(
)
120
cos(
)
cos(
cos
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(









t
t
t
t
t
t
I
V
t
p
t
i
t
v
t
i
t
v
t
i
t
v
t
p
m
m
c
cn
b
bn
a
an
power
ous
Instantane
 
)
cos(
)
cos(
2
1
cos
cos 




 



3cos cos(2 )
( ) cos(2 240 )
2
cos(2 480 )
m m
t
V I
p t t
t
  
 
 
 
 
 
 
 
 
   
  
)
120
sin(
sin
)
120
cos(
cos
)
120
cos(
)
120
sin(
sin
)
120
cos(
cos
)
120
cos(
cos
cos
0
)
120
cos(
)
120
cos(
cos























Proof
Lemma
5
.
0
)
120
cos( 

0
)
120
cos(
)
120
cos(
cos 



 


)
120
cos(
)
480
cos(
)
120
cos(
)
240
cos(














 t

4. THREE-PHASE CONNECTIONS
Positive sequence
a-b-c
Y-connected
loads Delta connected loads

5. SOURCE/LOAD CONNECTIONS
BALANCED Y-Y CONNECTION










120
|
|
120
|
|
0
|
|
p
cn
p
bn
p
an
V
V
V
V
V
V
Positive sequence
phase voltages
ab
V
bc
V
ca
V
Line voltages
 

























30
|
|
3
2
3
2
1
|
|
|
|
)
120
sin
120
(cos
1
|
|
120
|
|
0
|
|
p
p
p
p
p
p
bn
an
ab
V
j
V
V
j
V
V
V
V
V
V








210
|
|
3
90
|
|
3
p
ca
p
bc
V
V
V
V
Voltage
Line

 |
|
3 p
L V
V
Y
cn
c
Y
bn
b
Y
an
a
Z
V
I
Z
V
I
Z
V
I 

 ;
;










 120
|
|
;
120
|
|
;
|
| 

 L
c
L
b
L
a I
I
I
I
I
I
0



 n
c
b
a I
I
I
I For this balanced circuit it is enough to analyze one phase

6. Relationship between
phase and line voltages
LEARNING EXAMPLE For an abc sequence, balanced Y - Y three phase circuit



 30
208
ab
V
Determine the phase voltages
Balanced Y - Y
Positive sequence
a-b-c


 30
|
|
3 p
ab V
V










120
|
|
120
|
|
0
|
|
p
cn
p
bn
p
an
V
V
V
V
V
V
Positive sequence
phase voltages
)
30
30
(
3
|
|






 ab
an
V
V

30
by
lags ab
an V
V



 30
208
ab
V











60
120
180
120
60
120
an
bn
an
V
V
V
The phasor diagram could be rotated by any angle

7. LEARNING EXAMPLE For an abc sequence, balanced Y - Y three phase circuit
source 120( ) , 1 1 , 20 10
rms
phase line phase
V V Z j Z j
      
Determine line currents and load voltages
Because circuit is balanced
data on any one phase is
sufficient

0
120
Chosen
as reference
120 0
120 120
120 120
an
bn
cn
V
V
V
  
  
  
Abc sequence
rms
A
j
V
I an
aA
)
(
65
.
27
06
.
5
65
.
27
71
.
23
0
120
11
21











rms
A
I
rms
A
I
cC
bB
)
(
65
.
27
120
06
.
5
)
(
65
.
27
120
06
.
5















 57
.
26
36
.
22
)
10
20
( aA
aA
AN I
j
I
V
rms
V
VAN )
(
08
.
1
15
.
113 



rms
V
V
rms
V
V
CN
BN
)
(
92
.
118
15
.
113
)
(
08
.
121
15
.
113








8. LEARNING EXTENSION For an abc sequence, balanced Y - Y three phase circuit
voltages
line
the
Find
.
)
(
90
120 rms
V
Van 


Relationship between
phase and line voltages


 30
|
|
3 p
ab V
V

30
by
lags ab
an V
V
30
by
leads 
an
ab V
V
rms
V
Vab )
(
120
120
3 



rms
V
V
rms
V
V
ca
bc
)
(
240
120
3
)
(
0
120
3








voltages
phase
the
Find
.
)
(
0
208 rms
V
Vab 



30
by
lags ab
an V
V
rms
V
Van )
(
30
3
208




rms
V
V
rms
V
V
cn
bn
)
(
90
3
208
)
(
150
3
208








9. LEARNING EXTENSION For an abc sequence, balanced Y - Y three phase circuit
load 104.02 26.6 ( ) , 1 1 , 8 3
rms
phase line phase
V V Z j Z j
        
Determine source phase voltages
rms
V)
(
6
.
26
02
.
104 



8

3
j
Currents are not required. Use inverse
voltage divider
AN
an V
j
j
j
V
3
8
)
1
1
(
)
3
8
(















41
.
3
15
.
1
73
5
84
3
8
3
8
3
8
4
9 j
j
j
j
j


 30
120
an
V
Positive sequence
a-b-c







150
120
90
120
cn
bn
V
V

10. DELTA CONNECTED SOURCES
Relationship between
phase and line voltages


 30
|
|
3 p
ab V
V

30
by
lags ab
an V
V
















120
120
0
L
ca
L
bc
L
ab
V
V
V
V
V
V




















90
3
150
3
30
3
L
cn
L
bn
L
an
V
V
V
V
V
V















150
120
90
120
30
120
cn
bn
an
V
V
V
















180
208
60
208
60
208
ca
bc
ab
V
V
V
Example
Convert to an equivalent Y connection

11. LEARNING EXAMPLE Determine line currents and line voltages at the loads
Source is Delta connected.
Convert to equivalent Y
















120
120
0
L
ca
L
bc
L
ab
V
V
V
V
V
V




















90
3
150
3
30
3
L
cn
L
bn
L
an
V
V
V
V
V
V
Analyze one phase
rms
A
j
IaA )
(
14
.
49
38
.
9
2
.
4
1
.
12
30
)
3
/
208
(









rms
V
j
VAN )
(
71
.
30
65
.
118
19
.
49
38
.
9
)
4
12
( 









Determine the other phases using the balance
rms
A
I
rms
A
I
cC
bB
)
(
86
.
71
38
.
9
)
(
14
.
169
38
.
9










 30
|
|
3 p
ab V
V 3 118.65 0.71
AB
V    
3 118.65 120.71
3 118.65 119.29
BC
CA
V
V
   
   

12. LEARNING EXTENSION Compute the magnitude of the line voltage at the load
Source is Delta connected.
Convert to equivalent Y
















120
120
0
L
ca
L
bc
L
ab
V
V
V
V
V
V




















90
3
150
3
30
3
L
cn
L
bn
L
an
V
V
V
V
V
V
Analyze one phase





 30
120
1
.
4
1
.
10
4
10
j
j
VAN

10

1
.
0
j
Only interested in magnitudes!
rms
V
VAN )
(
57
.
118
90
.
10
77
.
10
120
|
| 



 30
|
|
3 p
ab V
V rms
V
VAB )
(
4
.
205
|
| 

13. DELTA-CONNECTED LOAD
Method 1: Solve directly










120
|
|
120
|
|
0
|
|
p
cn
p
bn
p
an
V
V
V
V
V
V
Positive sequence
phase voltages











210
|
|
3
90
|
|
3
30
|
|
3
p
ca
p
bc
p
ab
V
V
V
V
V
V






















120
|
|
120
|
|
|
|



I
Z
V
I
I
Z
V
I
I
Z
V
I
CA
CA
BC
BC
AB
AB
currents
phase
Load
BC
CA
cC
AB
BC
bB
CA
AB
aA
I
I
I
I
I
I
I
I
I






currents
Line
Method 2: We can also convert the delta
connected load into a Y connected one.
The same formulas derived for resistive
circuits are applicable to impedances
3


Z
ZY
case
Balanced











 
Z
L
AB
aA
L
aA
Y
an
aA Z
V
I
I
Z
V
I


 3
/
|
|
3
/
|
|
|
|
|
|
Z
L
Z
Z 


 |
|
Z

 


 30






30
|
|
3
|
|

line
line I
I
Line-phase current
relationship

14. 






30
|
|
3
|
|

line
line I
I
Line-phase current
relationship
ip
relationsh
voltage
phase
-
Line






30
|
|
3
|
|
phase
phase
V
V


LEARNING EXTENSION
currents
phase
the
Find
.
40
12 


aA
I










190
93
.
6
50
93
.
6
70
93
.
6
CA
BC
AB
I
I
I

15. Y


b
a
ab R
R
R 

)
(
|| 3
1
2 R
R
R
Rab 

3
2
1
3
1
2 )
(
R
R
R
R
R
R
R
R b
a





3
2
1
2
1
3 )
(
R
R
R
R
R
R
R
R c
b





3
2
1
3
2
1 )
(
R
R
R
R
R
R
R
R a
c





SUBTRACT THE FIRST TWO THEN ADD
TO THE THIRD TO GET Ra
a
b
b
a
R
R
R
R
R
R
R
R 1
3
3
1



c
b
c
b
R
R
R
R
R
R
R
R 1
2
1
2



REPLACE IN THE THIRD AND SOLVE FOR R1
Y
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
c
b
a











3
2
1
1
3
3
2
1
3
2
3
2
1
2
1











Y
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
a
a
c
c
b
b
a
c
a
c
c
b
b
a
b
a
c
c
b
b
a
3
2
1
tions
Transforma
Y
OF
REVIEW


3
3
2
1

 




R
R
R
R
R
R Y
Y



16. LEARNING EXAMPLE






 02
.
37
52
.
12
54
.
7
10 j
Z
Delta-connected load consists of 10-Ohm resistance in series
with 20-mH inductance. Source is Y-connected, abc sequence,
120-V rms, 60Hz. Determine all line and phase currents
rms
V
Van )
(
30
120 






 54
.
7
020
.
0
60
2
inductance
Z
rms
A
j
Z
V
I AB
AB )
(
98
.
22
60
.
16
54
.
7
10
60
3
120















30
|
|
3
|
|

line
line I
I
Line-phase current
relationship
ip
relationsh
voltage
phase
-
Line






30
|
|
3
|
|
phase
phase
V
V

 rms
A
IaA )
(
02
.
7
75
.
28 



rms
A
I
rms
A
I
CA
BC
)
(
98
.
142
60
.
16
)
(
02
.
97
60
.
16







rms
A
I
rms
A
I
cC
bB
)
(
98
.
112
75
.
28
)
(
02
.
127
75
.
28










 02
.
37
17
.
4
Y
Z
Alternatively, determine first the line currents
and then the delta currents

17. POWER RELATIONSHIPS

ip
relationsh
voltage
phase
-
Line






30
|
|
3
|
|
phase
phase
V
V








30
|
|
3
|
|

line
line I
I
Line-phase current
relationship
*
3
Total phase line
S V I

*
3 line
line
Total I
V
S 
*
3 

 I
V
S line
total
*
3 line
line
Total I
V
S 
line
V
line
I
Power factor angle
f 
f
line
line
total
f
line
line
total
I
V
Q
I
V
P


sin
|
||
|
3
cos
|
||
|
3


- Impedance angle

18. LEARNING EXAMPLE
lagging
20
angle
factor
power 



W
P
rms
V
V
total
line
1200
)
(
208
|
|
Determine the magnitude of the line
currents and the value of load impedance
per phase in the delta
f
line
line
total
f
line
line
total
I
V
Q
I
V
P


sin
|
||
|
3
cos
|
||
|
3


f
line
line
total I
V
P

cos
3
|
||
|
3
 rms
A
Iline )
(
54
.
3
|
| 







30
|
|
3
|
|

line
line I
I
Line-phase current
relationship
rms
A
I )
(
05
.
2
|
| 
 





 46
.
101
|
|
|
|
|
|
I
V
Z line



 20
46
.
101
Z
line
V
line
I
Power factor angle
f 
- Impedance angle


line
V

19. LEARNING EXAMPLE For an abc sequence, balanced Y - Y three phase circuit






 10
20
,
1
1
,
)
(
120
|
| j
Z
j
Z
V
V phase
line
rms
phase
source
Because circuit is balanced
data on any one phase is
sufficient

0
120
Chosen
as reference










120
120
120
120
0
120
an
bn
an
V
V
V
Abc sequence
rms
A
j
V
I an
aA
)
(
65
.
27
06
.
5
65
.
27
71
.
23
0
120
11
21











Determine real and reactive power per phase at the load and total real, reactive and
complex power at the source






 57
.
26
36
.
22
)
10
20
( aA
aA
AN I
j
I
V
rms
V
VAN )
(
08
.
1
15
.
113 










 65
.
27
06
.
5
08
.
1
15
.
113
*
aA
AN
phase I
V
S
rms
VA
j
Sphase )
(
09
.
256
512
57
.
26
54
.
572 











 65
.
27
06
.
5
0
120
*
aA
an I
V
S phase
source
VA
j
S
78
.
281
86
.
537
65
.
27
2
.
607





phase
source
)
(
78
.
281
3
)
(
86
.
537
3
VA
Q
W
P




source
total
source
total
)
(
6
.
1821
|
|
)
(
2
.
845
6
.
1613
VA
S
VA
j
Q
P
S





source
total
source
total
source
total
source
total

20. LEARNING EXTENSION A Y -Y balanced three-phase circuit has a line voltage of
208-Vrms. The total real power absorbed by the load is 12kW
at pf=0.8 lagging. Determine the per-phase impedance
of the load
ip
relationsh
voltage
phase
-
Line






30
|
|
3
|
|
phase
phase
V
V


*
3 phase
phase
Total I
V
S 


rms
V
Vphase )
(
120
3
208
|
| 


*
2
*
|
|
3
3
phase
phase
phase
phase
phase
total
Z
V
Z
V
V
S 











line
V
line
I
Power factor angle
Impedance angle




 87
.
36
cos
8
.
0 f
f
pf 

f
f
f
pf
S
Q
S
P
jQ
P
S



cos
sin
|
|
cos
|
|





kVA
pf
P
S total
total 15
|
| 




 88
.
2
|
|
|
|
3
|
|
2
total
phase
phase
S
V
Z



 87
.
36
88
.
2
pahse
Z
f


21. 




 30
120
1
.
4
1
.
10
4
10
j
j
VAN
Source is Delta connected.
Convert to equivalent Y
Analyze one phase

10

1
.
0
j
rms
V
VAN )
(
57
.
118
90
.
10
77
.
10
120
|
| 

LEARNING EXTENSION Determine real, reactive and complex power at both load
and source
*
2
* |
|
3
3
phase
AN
aA
AN
load
Z
V
I
V
S 



*
2
* |
|
3
3
phase
total
an
aA
an
source
Z
V
I
V
S 



2
2
2
2
4
10
)
4
10
(
|
57
.
118
|
3
4
10
|
57
.
118
|
3







j
j
2
2
2
2
)
1
.
4
(
)
1
.
10
(
)
1
.
4
1
.
10
(
|
120
|
3
1
.
4
1
.
10
|
120
|
3







j
j
)
496
1
.
1224
(
3
)
8
.
484
0
.
212
,
1
(
3
j
S
j
S
source
load






Polyphase