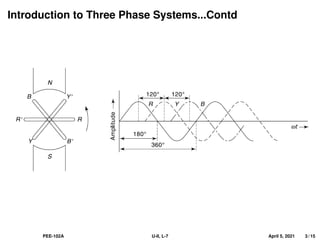
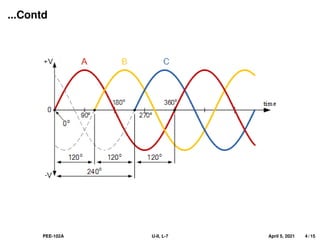
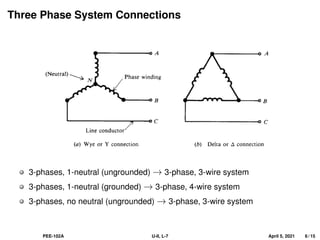
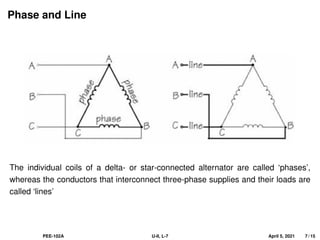
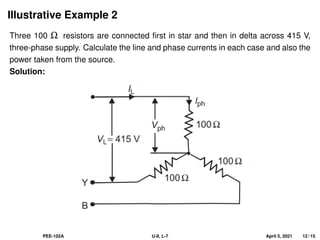
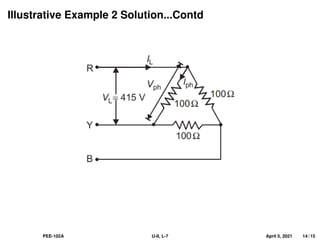
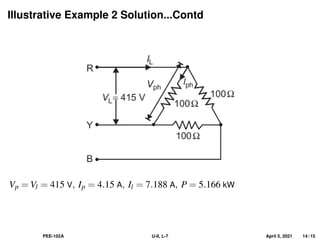
This document covers the fundamentals of three-phase electrical systems, highlighting the advantages over single-phase systems, such as reduced conductor material and improved machine efficiency. It explains key concepts including balanced systems, phase sequence, and the relationships between voltage, current, and power in three-phase systems. Additionally, it provides illustrative examples of calculations related to phase and line currents, as well as power drawn from the source.

1. PEE-102A
Fundamentals of Electrical Engineering
Lecture-7
Instructor:
Mohd. Umar Rehman
EES, University Polytechnic, AMU
April 5, 2021
PEE-102A U-II, L-7 April 5, 2021 1 / 15

2. Introduction to Three Phase Systems
A three-phase system may be considered as three separate single-phase sys-
tems displaced from each other by 120◦
A three-phase system is preferred over a single-phase system due to many
advantages like:
The amount of conductor material required is less for three-phase system.
Three phase machines have better performance and efficiency.
Three phase equipment has smaller size and weight.
A three phase AC voltage can be generated by rotating identical coils placed
with their axes at 120◦displaced from each other in a uniform magnetic field.
Such a system, and its associated wave forms are shown as follows
PEE-102A U-II, L-7 April 5, 2021 2 / 15

3. Introduction to Three Phase Systems...Contd
PEE-102A U-II, L-7 April 5, 2021 3 / 15

4. ...Contd
PEE-102A U-II, L-7 April 5, 2021 4 / 15

5. Remarks & Important Terms
The equations of three phase AC voltages can be written as:
vR = Vm sin(ωt)
vY = Vm sin(ωt −120◦
)
vB = Vm sin(ωt −240◦
)
= Vm sin(ωt +120◦
)
Balanced System: A balanced 3-phase supply system (star or delta con-
nected) is one in which the three phase voltages are equal in magnitude and
frequency but displaced 120° from one another. The above waveforms and
equations pertain to a balanced system.
Phase Sequence: The order in which the voltages in the three phases (or
coils) of an alternator reach their maximum positive values is called phase
sequence or phase order. The three phases or windings may be numbered as
(1, 2, 3) or lettered (a, b, c). However, it is a usual practice to name the three
phases after the three natural colours viz. red (R), yellow (Y) and blue (B). The
phase sequence is usually RYB.
PEE-102A U-II, L-7 April 5, 2021 5 / 15

6. Three Phase System Connections
3-phases, 1-neutral (ungrounded) → 3-phase, 3-wire system
3-phases, 1-neutral (grounded) → 3-phase, 4-wire system
3-phases, no neutral (ungrounded) → 3-phase, 3-wire system
PEE-102A U-II, L-7 April 5, 2021 6 / 15

7. Phase and Line
The individual coils of a delta- or star-connected alternator are called ‘phases’,
whereas the conductors that interconnect three-phase supplies and their loads are
called ‘lines’
PEE-102A U-II, L-7 April 5, 2021 7 / 15

8. Three Phase System Connections...Contd
Voltages between the phase and neutral are known as phase voltages.
These are denoted by van, vbn, vcn
In a balanced system, the magnitude of phase voltages is equal
|Van| = |Vbn| = |Vcn| = Vp
Voltages between the two phases or two lines are known as line voltages.
These are denoted by vab, vbc, vca
In a balanced system, the magnitude of line voltages is equal
|Vab| = |Vbc| = |Vca| = Vl
PEE-102A U-II, L-7 April 5, 2021 8 / 15

9. Voltage, Current & Power Relations in a 3-Phase System
In a balanced Y connected system, voltages and currents are related as fol-
lows:
Il = Ip, Vl =
√
3Vp
In a balanced ∆ connected system, voltages and currents are related as fol-
lows:
Vl = Vp, Il =
√
3Ip
Three phase Power in terms of line quantities:
P =
√
3VlIl cosφ
Three phase Power in terms of phase quantities:
P = 3VpIp cosφ
where, φ is the power factor angle between phase voltage and phase current.
PEE-102A U-II, L-7 April 5, 2021 9 / 15

10. Illustrative Example 1 (Refer to Lecture-6)
A single phase AC supply with peak value 282.8 V is supplying a current of 10 A to
an inductive load whose power factor is 0.8. Determine:
(a) RMS value of voltage
(b) Power factor angle
(c) Average Power delivered in Watts
PEE-102A U-II, L-7 April 5, 2021 10 / 15

11. Illustrative Example 1: Solution
(a) We know that
VRMS =
Vm
√
2
=
282.8
√
2
= 200 V
PEE-102A U-II, L-7 April 5, 2021 11 / 15

12. Illustrative Example 1: Solution
(a) We know that
VRMS =
Vm
√
2
=
282.8
√
2
= 200 V
(b) Power factor cosφ = 0.8 ⇒ φ = cos−1(0.8) = 37◦ (lagging)
(c) Average Power delivered in Watts
P = VI cosφ
= 200×10×0.8
= 1600 W = 1.6 kW
PEE-102A U-II, L-7 April 5, 2021 11 / 15

13. Illustrative Example 2
Three 100 Ω resistors are connected first in star and then in delta across 415 V,
three-phase supply. Calculate the line and phase currents in each case and also the
power taken from the source.
PEE-102A U-II, L-7 April 5, 2021 12 / 15

14. Illustrative Example 2
Three 100 Ω resistors are connected first in star and then in delta across 415 V,
three-phase supply. Calculate the line and phase currents in each case and also the
power taken from the source.
Solution:
PEE-102A U-II, L-7 April 5, 2021 12 / 15

15. Illustrative Example 2
Three 100 Ω resistors are connected first in star and then in delta across 415 V,
three-phase supply. Calculate the line and phase currents in each case and also the
power taken from the source.
Solution:
PEE-102A U-II, L-7 April 5, 2021 12 / 15

16. Illustrative Example 2 Solution...Contd
Phase voltage, Vp =
Vl
√
3
=
415
√
3
= 239.6 V
PEE-102A U-II, L-7 April 5, 2021 13 / 15

17. Illustrative Example 2 Solution...Contd
Phase voltage, Vp =
Vl
√
3
=
415
√
3
= 239.6 V
Phase current, Ip =
Vp
Rp
=
239.6
100
= 2.396 A
PEE-102A U-II, L-7 April 5, 2021 13 / 15

18. Illustrative Example 2 Solution...Contd
Phase voltage, Vp =
Vl
√
3
=
415
√
3
= 239.6 V
Phase current, Ip =
Vp
Rp
=
239.6
100
= 2.396 A
Line current, Il = Ip = 2.396 A
PEE-102A U-II, L-7 April 5, 2021 13 / 15

19. Illustrative Example 2 Solution...Contd
Phase voltage, Vp =
Vl
√
3
=
415
√
3
= 239.6 V
Phase current, Ip =
Vp
Rp
=
239.6
100
= 2.396 A
Line current, Il = Ip = 2.396 A
Power drawn, P = 3I2
pRp = 3×2.3962 ×100 = 1.722 kW
PEE-102A U-II, L-7 April 5, 2021 13 / 15

20. Illustrative Example 2 Solution...Contd
Phase voltage, Vp =
Vl
√
3
=
415
√
3
= 239.6 V
Phase current, Ip =
Vp
Rp
=
239.6
100
= 2.396 A
Line current, Il = Ip = 2.396 A
Power drawn, P = 3I2
pRp = 3×2.3962 ×100 = 1.722 kW
P = 3VpIp cosφ = 3×239.6×2.396 = 1.722 kW
PEE-102A U-II, L-7 April 5, 2021 13 / 15

21. Illustrative Example 2 Solution...Contd
Phase voltage, Vp =
Vl
√
3
=
415
√
3
= 239.6 V
Phase current, Ip =
Vp
Rp
=
239.6
100
= 2.396 A
Line current, Il = Ip = 2.396 A
Power drawn, P = 3I2
pRp = 3×2.3962 ×100 = 1.722 kW
P = 3VpIp cosφ = 3×239.6×2.396 = 1.722 kW
P =
√
3VlIl cosφ =
√
3×415×2.396 = 1.722 kW
PEE-102A U-II, L-7 April 5, 2021 13 / 15

22. Illustrative Example 2 Solution...Contd
PEE-102A U-II, L-7 April 5, 2021 14 / 15

23. Illustrative Example 2 Solution...Contd
Vp = Vl = 415 V, Ip = 4.15 A, Il = 7.188 A, P = 5.166 kW
PEE-102A U-II, L-7 April 5, 2021 14 / 15

24. Important Announcement
One mid-semester quiz will be conducted in online mode through Google Forms
next week i.e. 12th
April 2021, Monday.
Time: 1:00 PM - 1:30 PM, Max. Marks = 10
10 MCQs based on lectures 1-6.
Marks will be counted towards final assessment.
No requests for re-appearing or re-submission will be entertained.
Link to the quiz will be made available at 12:55 PM.
Response acceptance will be closed at 1:40 PM sharp.
PEE-102A U-II, L-7 April 5, 2021 15 / 15