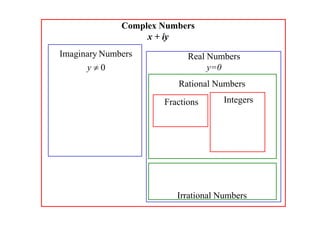
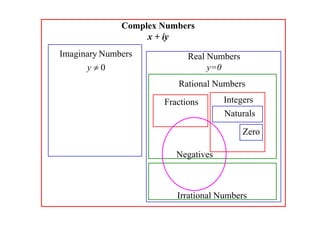
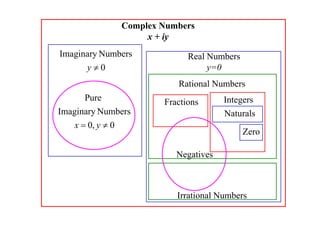
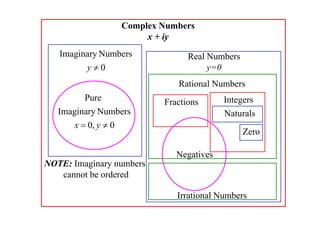
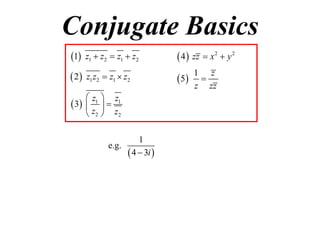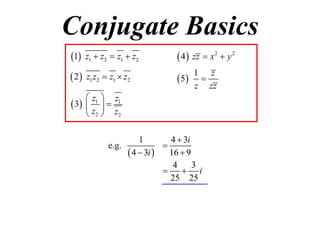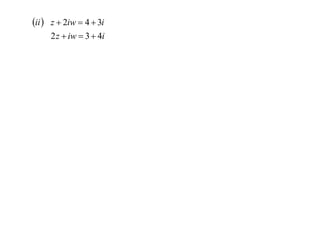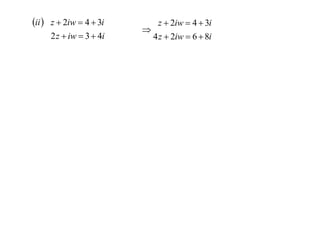The document discusses complex numbers. It begins by using an imaginary number, i, to solve the quadratic equation x2 + 1 = 0, which has no real solutions. It then defines i as the number that satisfies i2 = -1. All complex numbers can be written as z = x + iy, where x is the real part and iy is the imaginary part. Basic operations on complex numbers, such as addition, subtraction, multiplication and division, are discussed. The conjugate of a complex number z, denoted z*, is defined as z* = x - iy. Some key properties of conjugates are also outlined.

1. Complex Numbers
Solving Quadratics
x2 1  0

2. Complex Numbers
Solving Quadratics
x2 1  0
x 2  1
no real solutions

3. Complex Numbers
Solving Quadratics
x2 1  0
x 2  1
no real solutions
In order to solve this equation we define a new number

4. Complex Numbers
Solving Quadratics
x2 1  0
x 2  1
no real solutions
In order to solve this equation we define a new number
i  1
or
i 2  1
i is an imaginary number

5. Complex Numbers
Solving Quadratics
x2 1  0
x 2  1
no real solutions
In order to solve this equation we define a new number
i  1
or
i 2  1
i is an imaginary number
x 2  1
x   1
x  i

6. All complex numbers (z) can be written as; z = x + iy

7. All complex numbers (z) can be written as; z = x + iy
Definitions;
(1) All complex numbers contain a real and an imaginary part

8. All complex numbers (z) can be written as; z = x + iy
Definitions;
(1) All complex numbers contain a real and an imaginary part
Re z   x
Im z   y

9. All complex numbers (z) can be written as; z = x + iy
Definitions;
(1) All complex numbers contain a real and an imaginary part
Re z   x
Im z   y
e.g . z  3  5i

10. All complex numbers (z) can be written as; z = x + iy
Definitions;
(1) All complex numbers contain a real and an imaginary part
Re z   x
Im z   y
e.g . z  3  5i
Re z   3
Im z   5

11. All complex numbers (z) can be written as; z = x + iy
Definitions;
(1) All complex numbers contain a real and an imaginary part
Re z   x
Im z   y
e.g . z  3  5i
Re z   3
Im z   5
(2) If Re(z) = 0, then z is a pure imaginary number
e.g . 3i,6i

12. All complex numbers (z) can be written as; z = x + iy
Definitions;
(1) All complex numbers contain a real and an imaginary part
Re z   x
Im z   y
e.g . z  3  5i
Re z   3
Im z   5
(2) If Re(z) = 0, then z is a pure imaginary number
e.g . 3i,6i
(3) If Im(z) = 0, then z is a real number
3
e.g . ,  , e,4
4

13. All complex numbers (z) can be written as; z = x + iy
Definitions;
(1) All complex numbers contain a real and an imaginary part
Re z   x
Im z   y
e.g . z  3  5i
Re z   3
Im z   5
(2) If Re(z) = 0, then z is a pure imaginary number
e.g . 3i,6i
(3) If Im(z) = 0, then z is a real number
3
e.g . ,  , e,4
4
(4) Every complex number z = x + iy, has a complex conjugate
z  x  iy

14. All complex numbers (z) can be written as; z = x + iy
Definitions;
(1) All complex numbers contain a real and an imaginary part
Re z   x
Im z   y
e.g . z  3  5i
Re z   3
Im z   5
(2) If Re(z) = 0, then z is a pure imaginary number
e.g . 3i,6i
(3) If Im(z) = 0, then z is a real number
3
e.g . ,  , e,4
4
(4) Every complex number z = x + iy, has a complex conjugate
z  x  iy
z  2  7i
e.g . z  2  7i

15. Complex Numbers
x + iy

16. Complex Numbers
x + iy
Real Numbers
y=0

17. Complex Numbers
x + iy
Imaginary Numbers
y0
Real Numbers
y=0

18. Complex Numbers
x + iy
Imaginary Numbers
y0
Real Numbers
y=0
Rational Numbers
Irrational Numbers

19. Complex Numbers
x + iy
Imaginary Numbers
y0
Real Numbers
y=0
Rational Numbers
Fractions
Integers
Irrational Numbers

20. Complex Numbers
x + iy
Imaginary Numbers
y0
Real Numbers
y=0
Rational Numbers
Fractions
Integers
Naturals
Zero
Irrational Numbers

21. Complex Numbers
x + iy
Imaginary Numbers
y0
Real Numbers
y=0
Rational Numbers
Fractions
Integers
Naturals
Zero
Negatives
Irrational Numbers

22. Complex Numbers
x + iy
Imaginary Numbers
y0
Real Numbers
y=0
Rational Numbers
Pure
Imaginary Numbers
x  0, y  0
Fractions
Integers
Naturals
Zero
Negatives
Irrational Numbers

23. Complex Numbers
x + iy
Imaginary Numbers
y0
Real Numbers
y=0
Rational Numbers
Pure
Imaginary Numbers
x  0, y  0
Fractions
Integers
Naturals
Zero
Negatives
NOTE: Imaginary numbers
cannot be ordered
Irrational Numbers

24. Basic Operations
As i a surd, the operations with complex numbers are the same as surds

25. Basic Operations
As i a surd, the operations with complex numbers are the same as surds
Addition
4  3i    8  2i 
 4  i

26. Basic Operations
As i a surd, the operations with complex numbers are the same as surds
Addition
Subtraction
4  3i    8  2i 
4  3i    8  2i 
 4  i
 12  5i

27. Basic Operations
As i a surd, the operations with complex numbers are the same as surds
Addition
Subtraction
4  3i    8  2i 
4  3i    8  2i 
 4  i
 12  5i
Multiplication
4  3i  8  2i 

28. Basic Operations
As i a surd, the operations with complex numbers are the same as surds
Addition
Subtraction
4  3i    8  2i 
4  3i    8  2i 
 4  i
 12  5i
Multiplication
4  3i  8  2i 
 32  8i  24i  6i 2

29. Basic Operations
As i a surd, the operations with complex numbers are the same as surds
Addition
Subtraction
4  3i    8  2i 
4  3i    8  2i 
 4  i
 12  5i
Multiplication
4  3i  8  2i 
 32  8i  24i  6i 2
 32  32i  6
 26  32i

30. Basic Operations
As i a surd, the operations with complex numbers are the same as surds
Addition
Subtraction
4  3i    8  2i 
4  3i    8  2i 
 4  i
 12  5i
Multiplication
4  3i  8  2i 
 32  8i  24i  6i 2
 32  32i  6
 26  32i
Division (Realising The Denominator)
4  3i 
 8  2i 

31. Basic Operations
As i a surd, the operations with complex numbers are the same as surds
Addition
Subtraction
4  3i    8  2i 
4  3i    8  2i 
 4  i
 12  5i
Multiplication
4  3i  8  2i 
 32  8i  24i  6i 2
 32  32i  6
 26  32i
Division (Realising The Denominator)
4  3i 
 8  2i 

 8  2i   8  2i 
 32  8i  24i  6

64  4

32. Basic Operations
As i a surd, the operations with complex numbers are the same as surds
Addition
Subtraction
4  3i    8  2i 
4  3i    8  2i 
 4  i
 12  5i
Multiplication
4  3i  8  2i 
 32  8i  24i  6i 2
 32  32i  6
 26  32i
Division (Realising The Denominator)
4  3i 
 8  2i 

 8  2i   8  2i 
 32  8i  24i  6

64  4
 38  16i

68
 19 8

 i
34 34

33. Conjugate Basics
1
z1  z2  z1  z2

34. Conjugate Basics
1
z1  z2  z1  z2
 2
z1 z2  z1  z2
 z1  z1
 3   
 z2  z2

35. Conjugate Basics
1
z1  z2  z1  z2
 2
z1 z2  z1  z2
 z1  z1
 3   
 z2  z2
 4  zz  x 2  y 2

36. Conjugate Basics
1
z1  z2  z1  z2
 4  zz  x 2  y 2
 2
z1 z2  z1  z2
1 z
 5 
z zz
 z1  z1
 3   
 z2  z2

37. Conjugate Basics
1
z1  z2  z1  z2
 4  zz  x 2  y 2
 2
z1 z2  z1  z2
1 z
 5 
z zz
 z1  z1
 3   
 z2  z2
1
e.g.
 4  3i 

38. Conjugate Basics
1
z1  z2  z1  z2
 4  zz  x 2  y 2
 2
z1 z2  z1  z2
1 z
 5 
z zz
 z1  z1
 3   
 z2  z2
1
4  3i

e.g.
 4  3i  16  9
4
3

 i
25 25

39. Complex Equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal
i.e. If a1  b1i  a2  b2i
then
a1  a2
b1  b2

40. Complex Equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal
i.e. If a1  b1i  a2  b2i
then
a1  a2
b1  b2

41. Complex Equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal
i.e. If a1  b1i  a2  b2i
then
a1  a2
b1  b2
e.g . (i)
 2  3i  x  iy    4  2i 

42. Complex Equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal
i.e. If a1  b1i  a2  b2i
then
a1  a2
b1  b2
e.g . (i)
 2  3i  x  iy    4  2i 
2 x  2iy  3ix  3 y  4  2i

43. Complex Equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal
i.e. If a1  b1i  a2  b2i
then
a1  a2
b1  b2
e.g . (i)
 2  3i  x  iy    4  2i 
2 x  2iy  3ix  3 y  4  2i
 2 x  3 y  4 and 3 x  2 y  2

44. Complex Equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal
i.e. If a1  b1i  a2  b2i
then
a1  a2
b1  b2
e.g . (i)
 2  3i  x  iy    4  2i 
2 x  2iy  3ix  3 y  4  2i
 2 x  3 y  4 and 3 x  2 y  2
4x  6 y  8

9 x  6 y  6

45. Complex Equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal
i.e. If a1  b1i  a2  b2i
then
a1  a2
b1  b2
e.g . (i)
 2  3i  x  iy    4  2i 
2 x  2iy  3ix  3 y  4  2i
 2 x  3 y  4 and 3 x  2 y  2
4x  6 y  8

9 x  6 y  6
5x
 14
14
x
5

46. Complex Equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal
i.e. If a1  b1i  a2  b2i
then
a1  a2
b1  b2
e.g . (i)
 2  3i  x  iy    4  2i 
2 x  2iy  3ix  3 y  4  2i
 2 x  3 y  4 and 3 x  2 y  2
14
16
, y
x  
5
5
4x  6 y  8

9 x  6 y  6
5x
 14
14
x
5

47. ii  z  2iw  4  3i
2 z  iw  3  4i

48. ii  z  2iw  4  3i
2 z  iw  3  4i

z  2iw  4  3i
4 z  2iw  6  8i

49. ii  z  2iw  4  3i
2 z  iw  3  4i

z  2iw  4  3i
4 z  2iw  6  8i
 2  5i
3z
2 5
z  i
3 3

50. ii  z  2iw  4  3i
2 z  iw  3  4i
2 5
  i  2iw  4  3i
3 3
10 4
2iw   i
3 3
10 4
w 
6i 6
2 5
  i
3 3

z  2iw  4  3i
4 z  2iw  6  8i
 2  5i
3z
2 5
z  i
3 3

51. ii  z  2iw  4  3i
2 z  iw  3  4i

2 5
  i  2iw  4  3i
3 3
10 4
2iw   i
3 3
10 4
w 
6i 6
2 5
  i
3 3
2 5
2 5
w  i , z  i
3 3
3 3
z  2iw  4  3i
4 z  2iw  6  8i
 2  5i
3z
2 5
z  i
3 3

52. Cambridge: Exercise 1A; 1 to 10 ace etc, 11bd, 13 to 20
Patel: Exercise 4A; 28 ac