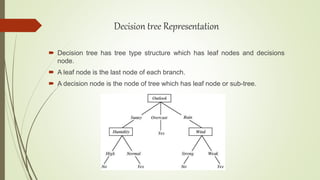
The document discusses decision tree induction, which is a popular tool for classification and prediction. It describes how decision trees work by having internal decision nodes that split the data into branches, which end at leaf nodes that provide a class label or prediction. It also covers different algorithms for building decision trees like ID3, C4.5, and CART. The key steps in decision tree induction include selecting attributes to split on using metrics like information gain or Gini index, and pruning the fully grown tree to avoid overfitting.

1. Made by: -
Deopura karan 130410107014
Submitted to: -
Mitali sonar

3. Decision tree Induction
 Training dataset should be class-labelled for learning of decision.
 A decision-tree represent rules and it is very popular tool for classification
and prediction
 Rules are easy to understand and can be directly used in SQL to retrieve
records
 There are many algorithm to build decision tree:
o ID3(Iterative Dichotomiser 3)
o C4.5
o CART(Classification and Regression Tree)
o CHAID(Chi-squared Automatic Interaction Detector)

4.  Decision tree has tree type structure which has leaf nodes and decisions
node.
 A leaf node is the last node of each branch.
 A decision node is the node of tree which has leaf node or sub-tree.
Decision tree Representation

5.  Attribute for decision tree are selected by one of the following method:
1. Gini index(IBM IntelligentMiner)
2. Information Gain(ID3/C4.5)
3. Gain ratio
 Attribute are categories into two part:
1. Attribute whose domain is numerical are called numerical attribute
2. Attribute whose domain is non-numerical are called categorical attribute.
Attribute Selection

6.  It can be adapted for categorical attributes
 Uses in CART, SPRINT and IBM’s Intelligent miner System
 Formula for Gini index is
 For a valued attribute, the attribute providing the smallest gini is chosen to
split the node.
Gini index

7.  It can be adapted for continuous-valued attribute as well as categorical
data.
 Attribute which has highest information gain is selected for split.
 If Si contain pi examples of P and ni examples of N, the entropy to classify
object is
Information gain

8.  Expected amount of information needed to assign a class to a randomly
drawn object in S
 Calculate information gain i.e. gain(A) : Measure reduction in entropy
achieved because of split.
𝑮𝒂𝒊𝒏 𝑨 = 𝑰 𝒑, 𝒏 − 𝑬(𝑨)
Entropy

10.  Decision trees are able to generate understandable rules
 Perform classification without requiring much computation
 Handle categorical as well as continuous variable
 Provide clear induction of which fields are most important
Strength of decision tree
Weakness of decision tree
 Not suitable for prediction of continuous attribute
 Computationally expensive to train

11.  Two types
1. Prepruning
 Start pruning in the beginning while building the tree itself
 Stop the tree construction in early stage
 Avoid splitting node by checking the threshold
2. Postpruning
 Build the tree then start pruning
 Use different set of data than training dataset to get best pruned tree
Tree Pruning

12. A Training set
Age Car Type Risk
23 Family High
17 Sports High
43 Sports High
68 Family Low
32 Truck Low
20 Family High

13. Decision Tree
Age < 25
Car Type in {sports}
High
High Low