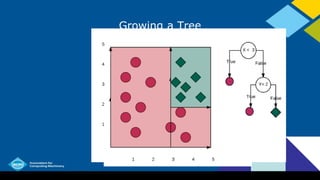
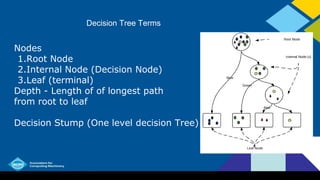
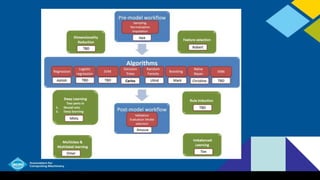
This document discusses decision trees, including: - Decision trees are tree-like graphs used for decision support modeling. There are classification trees for categorical variables and regression trees for continuous variables. - Nodes in a decision tree include the root node, internal decision nodes, and leaf nodes. The depth is the longest path from root to leaf. - Common algorithms for building decision trees include ID3, C4.5, C5.0, and CART. They use criteria like information gain, Gini index, and classification error to determine the best attributes to split on. - Decision trees can be prone to overfitting without pruning. Strategies like prepruning and postpruning are used to prevent over

1. Advanced Machine Learning with Python
Session 9 :Decision Trees
SIGKDD
Carlos Santillan
Bentley Systems Inc
csantill@gmail.com

4. Decision Trees
A tree-like graph decision support model

5. Growing a Tree

6. Types of Decision Trees
There are two main Types
• Classification Tree (Categorical Value Decision Tree)
• Regression Tree (Continuous Variable Decision Tree)
CART (Classification and Regression Tree) Used to refer to both
The type of a Decision tree is based on the type of the target Variable

7. Nodes
1.Root Node
2.Internal Node (Decision Node)
3.Leaf (terminal)
Depth - Length of of longest path
from root to leaf
Decision Stump (One level decision Tree)
Decision Tree Terms

8. Decision Tree Algorithm
The basic greedy algorithm is as follows:
Start at Node find “best attribute” to split at
Repartition N into N1, N2, … according to best split
Repeat for each Node N until “stop condition” is met
Growing an optimal Decision Tree is an NP-complete
Problem
Fortunately greedy algorithms have good accuracy and
performance

9. What is the “Best Attribute” to split
There are different criteria that can be used to determine what
is the best attribute to split.
• Information Gain
• Gini Index
• Classification Error
• Gain Ratio (Normalized Information Gain)
• Variance Reduction

10. Purity

11. Entropy
Def: Measure of Impurity in our sample
• Entropy =0 (All elements are same class)
• Entropy =1 (All elements evenly split between classes)

12. Information Gain
Information Gain = Entropy (Parent) - [ Weighted Average]
Entropy (Children)
If we Split X < 4
• Entropy < 4 = 0.86
• Entropy > 4 = 0
Information Gain = 0.95 - 14/16 (0.86) - (2/16) (0)
Information Gain = 0.19

13. Information Gain
IG = Entropy (Parent) - [ Weighted Average] Entropy (Children)
If we Split X < 3
• Entropy < 3 = 0
• Entropy > 3 = 0.811
Information Gain = 0.95 - 8/16 (0) - (2/16) (0.811)
Information Gain = 0.8486

14. GINI Index
Definition : Expected error rate
• GINI =0 (All elements are same class)
• GINI =0.5 (All elements evenly split between classes)

15. GINI Gain
If we Split X < 4
• Gini < 4 = 0.4081
• Gini > 4 = 0
Gini Gain = 0.4687 - 10/16 (0.4081) - (0/16) (0)
Gini Gain = 0.2136

16. GINI Gain
If we Split X < 3
• Gini< 3 = 0
• Gini > 3 = 0.375
Gini Gain = 0.4687 - 8/16 (0) - (2/16) (0.375)
Gini Gain = 0.421825

17. When to use which?
● Gini for continuous attributes
● Entropy for categorical.
● Entropy is slower to calculate than GINI
● Gini may fail with very small probability
● Difference between the two is theoretically around 2%

18. When to stop growing?
• All data points at leaf are pure
• When tree a reaches depth k
• Number of cases in node less that minimum number of cases
• Splitting criteria less than certain threshold

19. Pruning
Prevent over fitting
Smaller trees may be more accurate
Strategies:
• Prepruning : Stop growing when information becomes
unreliable
• Postpruning : fully grow a tree and remove unreliable parts
Note: Pruning currently not supported by scikit

20. Algorithms
ID3 (Iterative Dichotomiser 3) Greedy algorithm, categorical
(entropy)
C4.5 Improves on ID3 support categorical and continuous
(entropy)
C5.0 (See5)
CART similar to C4.5 (Gini Impurity)

21. Pros
• Easy to Understand (white box)
• Supports both Numerical and Categorical data
• Fast (greedy) algorithms
• Performs well with large datasets
• Accurate
• Feature importance

22. Cons
• Without pruning/Cross-validation Prone to overfitting
• Information gain biased toward features with a lot of classes
• Sensitive to changes in the data

23. DEMO

24. Resources
• https://github.com/csantill/AustinSIGKDD-DecisionTrees
• Decision Forests for Classification, Regression, Density
Estimation, Manifold Learning and Semi-Supervised Learning
• Classification and Regression Trees
• A Visual Introduction to Machine Learning
• A Complete Tutorial on Tree Based Modeling from Scratch
• Theoretical Comparison between the Gini Index and
Information Gain Criteria

25. Thank You
Carlos Santillan