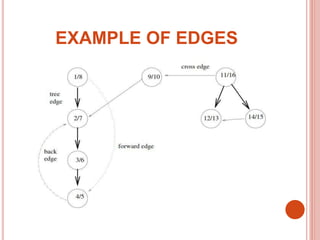
Depth-first search (DFS) is an algorithm that explores all the vertices reachable from a starting vertex by traversing edges in a depth-first manner. DFS uses a stack data structure to keep track of vertices to visit. It colors vertices white, gray, and black to indicate their status. DFS runs in O(V+E) time and can be used for applications like topological sorting and finding strongly connected components. The edges discovered during DFS can be classified as tree, back, forward, or cross edges based on the order in which vertices are discovered.

1. DEPTH FIRST
SEARCH [DFS]
By,
K.B.Snega,M.sc(cs).,

2. INTRODUCTION
 A depth-first search (DFS) explores a path all the
way to a leaf before backtracking and exploring
another path.
 For example, after searching A, then B, then D, the
search backtracks and tries another path from B.
 Node are explored in the order A B D E H L M N I O
P C F G J K Q. L M N O P N will be found before
J.

3. INTRO….
 To keep track of progress DFS colors each vertex
white, gray or black. Initially all the vertices are
colored white. Then they are colored gray when
discovered. Finally colored black when finished.
 Besides creating depth first forest DFS also
timestamps each vertex. Each vertex goes through
two time stamps:
 Discover time d[u]: when u is first discovered
Finish time f[u]: when backtrack from u or finished
u
f[u] > d[u]

4. DFS: ALGORITHM
DFS: Algorithm
DFS(G)
1. for each vertex u in G
2. color[u]=white
3. ᴨ[u]=NIL
4. time=0
5. for each vertex u in G
6. if (color[u]==white)
7. DFS-VISIT(G,u)

5. ALGO(CONT…)
DFS-VISIT(u)
1. time = time + 1
2. d[u] = time
3. color[u]=gray
4. for each v € Adj(u) in G do
5. if (color[v] = =white)
6. ᴨ [v] = u;
7. DFS-VISIT(G,v);
8. color[u] = black
9. time = time + 1;
10. f[u]= time;

6. DFS: COMPLEXITY ANALYSIS
 Initialization complexity is O(V)
 DFS_VISIT is called exactly once for each vertex
 And DFS_VISIT scans all the edges which causes
cost of O(E)
 Thus overall complexity is O(V + E)

7. DFS: APPLICATION
 Topological Sort
 Strongly Connected Component

8. CLASSIFICATION OF EDGES
 Tree edge: Edge (u,v) is a tree edge if v was first
discovered by exploring edge (u,v). White color
indicates tree edge.
 Back edge: Edge (u,v) is a back edge if it
connects a vertex u to a ancestor v in a depth
first tree. Gray color indicates back edge.
 Forward edge: Edge (u,v) is a forward edge if it
is non-tree edge and it connects a vertex u to a
descendant v in a depth first tree. Black color
indicates forward edge.
 Cross edge: rest all other edges are called the
cross edge. Black color indicates forward edge.

9. EXAMPLE OF EDGES

10. THEOREM DERIVED FROM DFS
 Theorem 1: In a depth first search of an undirected
graph G, every edge of G is either a tree edge or
back edge.
 Theorem 2: A directed graph G is acyclic if and
only if a depth-first search of G yields no back
edges.