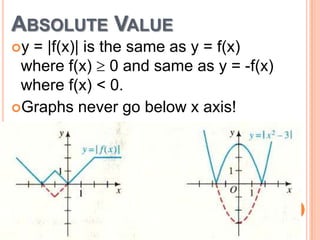
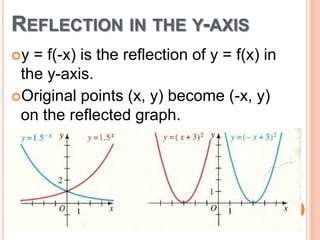
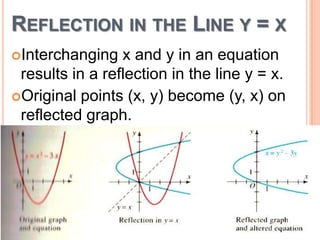
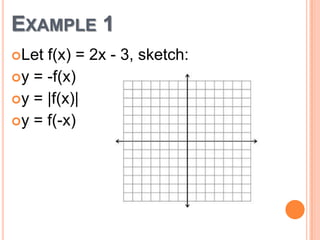
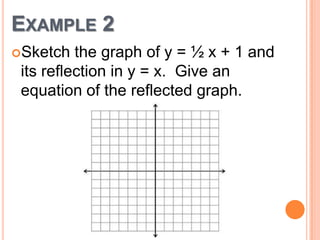
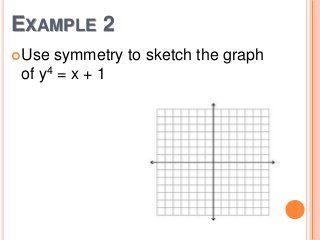
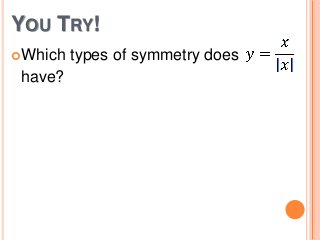This document discusses reflecting graphs and using symmetry to sketch graphs. It defines reflecting graphs across the x-axis, y-axis, and line y=x. Absolute value graphs are discussed. Even and odd functions are classified. Examples are provided of reflecting simple functions and using symmetry to sketch more complex graphs like cubics and quartics. Methods for determining if a function has symmetry across the x-axis, y-axis, line y=x, or origin are outlined.

1. 4-3 REFLECTING GRAPHS/
SYMMETRY
Objectives:
1. Reflect graphs
2. Use symmetry to sketch graphs
3. Classify even and odd functions

2. REFLECTION IN THE X-AXIS
y
= -f(x) is the reflection of y = f(x) in
the x-axis.
Original points (x, y) become (x, -y)
on the reflected graph.

3. ABSOLUTE VALUE
y
= |f(x)| is the same as y = f(x)
where f(x) 0 and same as y = -f(x)
where f(x) < 0.
Graphs never go below x axis!

4. REFLECTION IN THE Y-AXIS
y
= f(-x) is the reflection of y = f(x) in
the y-axis.
Original points (x, y) become (-x, y)
on the reflected graph.

5. REFLECTION IN THE LINE Y = X
Interchanging
x and y in an equation
results in a reflection in the line y = x.
Original points (x, y) become (y, x) on
reflected graph.

6. EXAMPLE 1
Let
f(x) = 2x - 3, sketch:
y = -f(x)
y = |f(x)|
y = f(-x)

7. EXAMPLE 2
Sketch
the graph of y = ½ x + 1 and
its reflection in y = x. Give an
equation of the reflected graph.

8. SYMMETRY
of symmetry – a line that divides
a graph such that it is a perpendicular
bisector of segments joining paired
points
Axis

9. POINT OF SYMMETRY
A
point O is a point of symmetry if it is
the midpoint of the segments joining
each pair of points on the graph.

10. QUADRATICS AND CUBICS
Parabolas
Axis
(y = ax2 + bx + c)
of symmetry at
Cubics
Point
(y = ax3 + bx2 + cx + d)
of symmetry at

11. X-AXIS SYMMETRY
(x,
-y) is on graph whenever (x, y) is.
Test:
Substitute –y for y.
If new equation = original, it has x-axis
symmetry.

12. Y-AXIS SYMMETRY
(-x,
y) is on graph whenever (x, y) is.
Test:
Substitute –x for x.
If new equation = original, it has y-axis
symmetry.

13. Y = X SYMMETRY
(y,
x) is on graph whenever (x, y) is.
Test:
Interchange x and y.
If new equation = original, it has y = x
symmetry.

14. ORIGIN SYMMETRY
(-x,
-y) is on graph whenever (x, y) is.
Test:
Substitute –x for x and –y for y.
If new equation = original, it has origin
symmetry.

15. EXAMPLE 1
Test
the equation to see which
kind(s) of symmetry it has.
x2 + xy = 4
|x|
+ |y| = 1

16. YOU TRY!
Which
have?
types of symmetry does

17. EXAMPLE 2
Use symmetry
of y4 = x + 1
to sketch the graph

18. EXAMPLE 3
Find
the point of symmetry of the
graph of f(x) = -x3 + 15x2 – 48x + 45
The
function has a local min at (2, 1).
Where does a local max occur?