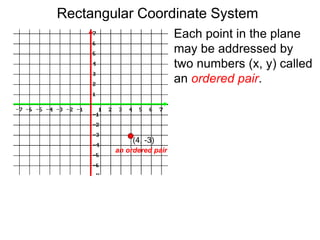
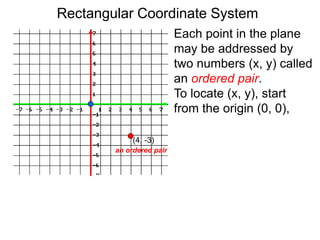
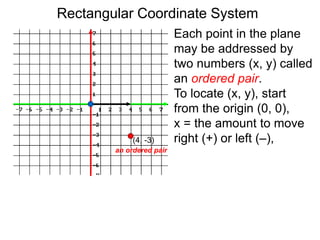
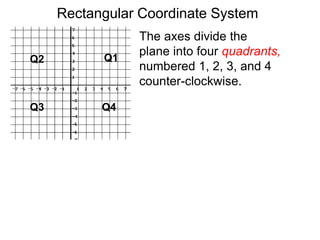
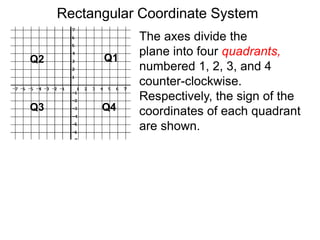
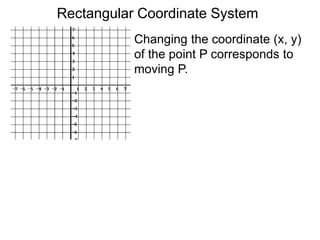
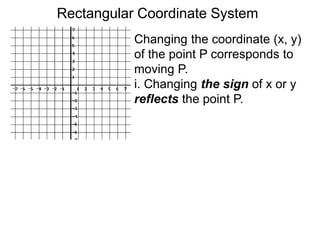
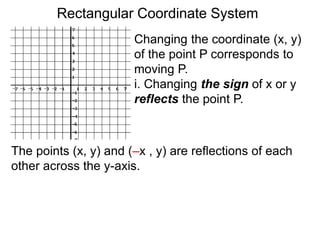
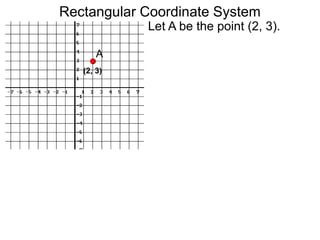
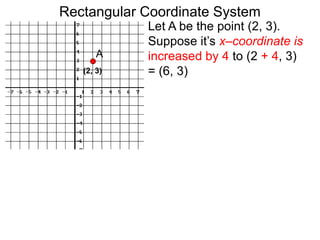
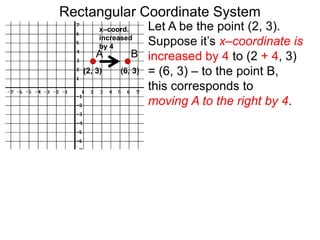
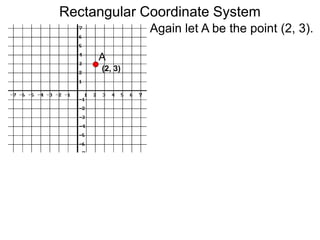
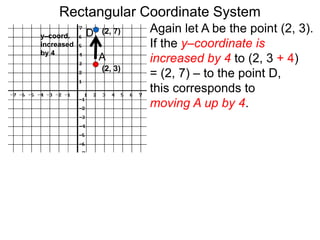
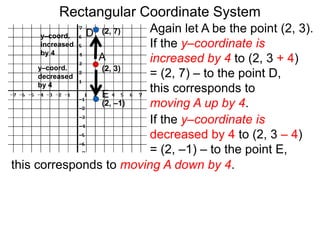
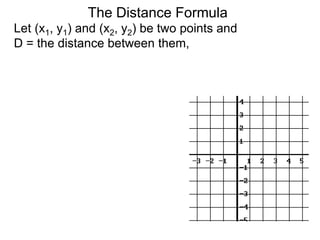
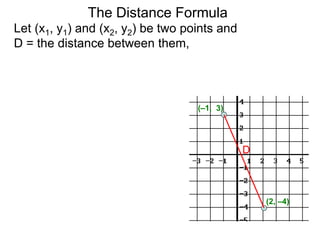
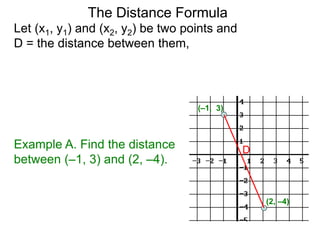
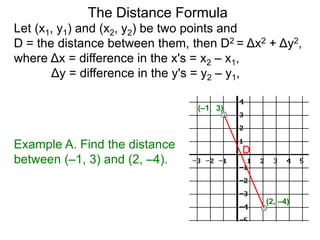
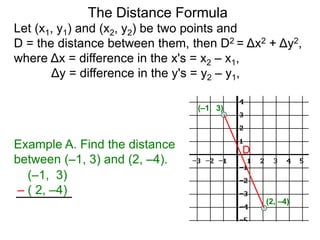
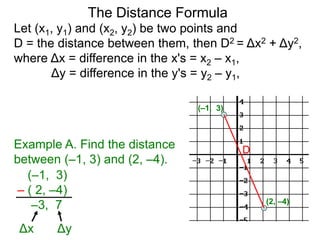
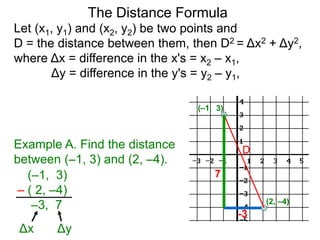
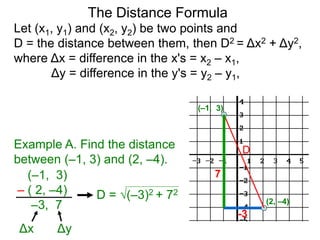
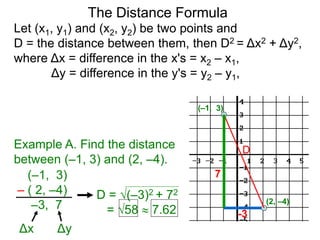
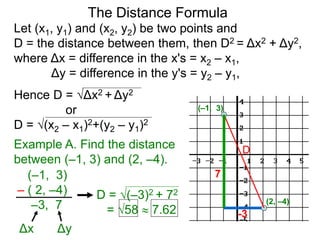
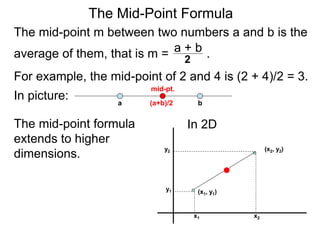
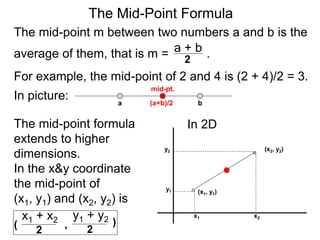
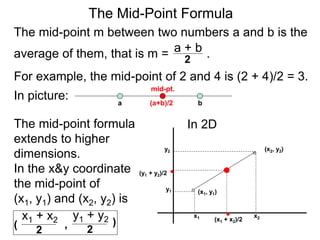
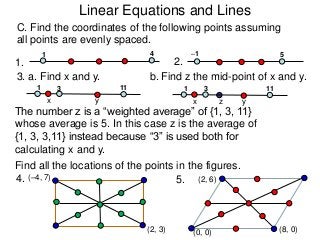
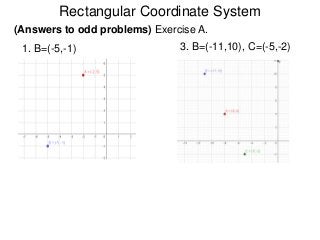
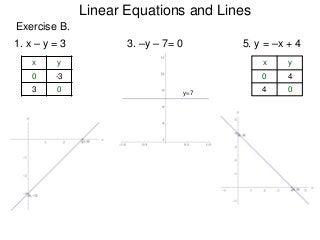
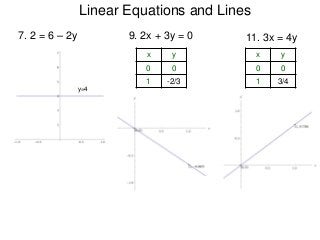
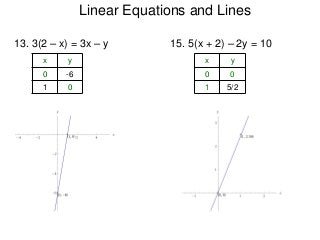
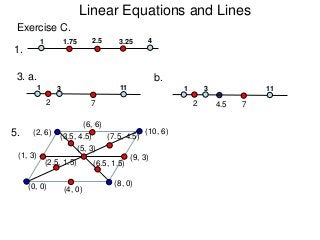
The document describes the rectangular coordinate system. Each point in the plane can be located using an ordered pair (x, y) representing horizontal and vertical distances from the origin. The x-axis represents horizontal distance and the y-axis represents vertical distance. Changing the x-value moves a point right or left, and changing the y-value moves a point up or down. The four quadrants are defined by the positive and negative x and y axes. Reflecting a point across an axis results in another point with the same distances but opposite sign for the axis coordinate.

1. Rectangular Coordinate System

2. Rectangular Coordinate System
Each point in the plane
may be addressed by
two numbers (x, y) called
an ordered pair.

3. Rectangular Coordinate System
Each point in the plane
may be addressed by
two numbers (x, y) called
an ordered pair.
(4, -3)
an ordered pair

4. Rectangular Coordinate System
Each point in the plane
may be addressed by
two numbers (x, y) called
an ordered pair.
To locate (x, y), start
from the origin (0, 0),
(4, -3)
an ordered pair

5. Rectangular Coordinate System
Each point in the plane
may be addressed by
two numbers (x, y) called
an ordered pair.
To locate (x, y), start
from the origin (0, 0),
x = the amount to move
right (+) or left (–),(4, -3)
an ordered pair

6. Rectangular Coordinate System
Each point in the plane
may be addressed by
two numbers (x, y) called
an ordered pair.
To locate (x, y), start
from the origin (0, 0),
x = the amount to move
right (+) or left (–),
y = the amount to move
up (+) or down (–).
(4, -3)
an ordered pair

7. For example, the point corresponding to (4, -3) is
4 right, and 3 down from the origin.
Rectangular Coordinate System
Each point in the plane
may be addressed by
two numbers (x, y) called
an ordered pair.
To locate (x, y), start
from the origin (0, 0),
x = the amount to move
right (+) or left (–),
y = the amount to move
up (+) or down (–).
(4, -3)
4 right
3 down
an ordered pair

8. For example, the point corresponding to (4, -3) is
4 right, and 3 down from the origin.
Rectangular Coordinate System
Each point in the plane
may be addressed by
two numbers (x, y) called
an ordered pair.
To locate (x, y), start
from the origin (0, 0),
x = the amount to move
right (+) or left (–),
y = the amount to move
up (+) or down (–).
Points on the x-axis have the form (#, 0)
(#, 0)
(4, -3)
4 right
3 down
an ordered pair

9. For example, the point corresponding to (4, -3) is
4 right, and 3 down from the origin.
Rectangular Coordinate System
Each point in the plane
may be addressed by
two numbers (x, y) called
an ordered pair.
To locate (x, y), start
from the origin (0, 0),
x = the amount to move
right (+) or left (–),
y = the amount to move
up (+) or down (–).
Points on the x-axis have the form (#, 0) and
points on the y-axis have the form (0, #).
(#, 0)
(0, #)
(4, -3)
4 right
3 down
an ordered pair

10. The axes divide the
plane into four quadrants,
numbered 1, 2, 3, and 4
counter-clockwise.
Rectangular Coordinate System

11. The axes divide the
plane into four quadrants,
numbered 1, 2, 3, and 4
counter-clockwise.
Q1Q2
Q3 Q4
Rectangular Coordinate System

12. The axes divide the
plane into four quadrants,
numbered 1, 2, 3, and 4
counter-clockwise.
Respectively, the sign of the
coordinates of each quadrant
are shown.
Q1Q2
Q3 Q4
Rectangular Coordinate System

13. The axes divide the
plane into four quadrants,
numbered 1, 2, 3, and 4
counter-clockwise.
Respectively, the sign of the
coordinates of each quadrant
are shown.
Q1Q2
Q3 Q4
(+,+)
Rectangular Coordinate System

14. The axes divide the
plane into four quadrants,
numbered 1, 2, 3, and 4
counter-clockwise.
Respectively, the sign of the
coordinates of each quadrant
are shown.
Q1Q2
Q3 Q4
(+,+)(–,+)
Rectangular Coordinate System

15. The axes divide the
plane into four quadrants,
numbered 1, 2, 3, and 4
counter-clockwise.
Respectively, the sign of the
coordinates of each quadrant
are shown.
Q1Q2
Q3 Q4
(+,+)(–,+)
(–,–) (+,–)
Rectangular Coordinate System

16. Changing the coordinate (x, y)
of the point P corresponds to
moving P.
Rectangular Coordinate System

17. Changing the coordinate (x, y)
of the point P corresponds to
moving P.
i. Changing the sign of x or y
reflects the point P.
Rectangular Coordinate System

18. Changing the coordinate (x, y)
of the point P corresponds to
moving P.
i. Changing the sign of x or y
reflects the point P.
Rectangular Coordinate System
The points (x, y) and (–x , y) are reflections of each
other across the y-axis.

19. Rectangular Coordinate System
The points (x, y) and (–x , y) are reflections of each
other across the y-axis.
(5,4)(–5,4) Changing the coordinate (x, y)
of the point P corresponds to
moving P.
i. Changing the sign of x or y
reflects the point P.

20. Rectangular Coordinate System
The points (x, y) and (–x , y) are reflections of each
other across the y-axis.
The points (x, y) and (x , –y) are reflections of each
other across the x-axis.
(5,4)(–5,4) Changing the coordinate (x, y)
of the point P corresponds to
moving P.
i. Changing the sign of x or y
reflects the point P.

21. Rectangular Coordinate System
The points (x, y) and (–x , y) are reflections of each
other across the y-axis.
The points (x, y) and (x , –y) are reflections of each
other across the x-axis.
(5,4)(–5,4)
(5, –4)
Changing the coordinate (x, y)
of the point P corresponds to
moving P.
i. Changing the sign of x or y
reflects the point P.

22. Rectangular Coordinate System
The points (x, y) and (–x , y) are reflections of each
other across the y-axis.
The points (x, y) and (x , –y) are reflections of each
other across the x-axis.
The points (x, y) and (–x , –y) are reflections of each
other across the origin.
(5,4)(–5,4)
(5, –4)
Changing the coordinate (x, y)
of the point P corresponds to
moving P.
i. Changing the sign of x or y
reflects the point P.

23. Rectangular Coordinate System
The points (x, y) and (–x , y) are reflections of each
other across the y-axis.
The points (x, y) and (x , –y) are reflections of each
other across the x-axis.
The points (x, y) and (–x , –y) are reflections of
each other across the origin.
(5,4)(–5,4)
(5, –4)(–5, –4)
Changing the coordinate (x, y)
of the point P corresponds to
moving P.
i. Changing the sign of x or y
reflects the point P.

24. Rectangular Coordinate System
The points (x, y) and (–x , y) are reflections of each
other across the y-axis.
The points (x, y) and (x , –y) are reflections of each
other across the x-axis.
The points (x, y) and (–x , –y) are reflections of
each other across the origin.
(5,4)(–5,4)
(5, –4)(–5, –4)
Changing the coordinate (x, y)
of the point P corresponds to
moving P.
i. Changing the sign of x or y
reflects the point P.
ii. Changing the value of x or y
moves P right/left/up/down.

25. Let A be the point (2, 3).
Rectangular Coordinate System
A
(2, 3)

26. Let A be the point (2, 3).
Suppose its x–coordinate is
increased by 4 to (2 + 4, 3)
= (6, 3)
Rectangular Coordinate System
A
(2, 3)

27. Let A be the point (2, 3).
Suppose its x–coordinate is
increased by 4 to (2 + 4, 3)
= (6, 3) – to the point B,
this corresponds to
moving A to the right by 4.
Rectangular Coordinate System
A B
x–coord.
increased
by 4
(2, 3) (6, 3)

28. Let A be the point (2, 3).
Suppose its x–coordinate is
increased by 4 to (2 + 4, 3)
= (6, 3) – to the point B,
this corresponds to
moving A to the right by 4.
Rectangular Coordinate System
A B
Similarly if the x–coordinate is
decreased by 4 to (2 – 4, 3)
= (–2, 3) – to the point C,
C
x–coord.
increased
by 4
x–coord.
decreased
by 4
(2, 3) (6, 3)(–2, 3)
this corresponds to moving A to the left by 4.

29. Let A be the point (2, 3).
Suppose its x–coordinate is
increased by 4 to (2 + 4, 3)
= (6, 3) – to the point B,
this corresponds to
moving A to the right by 4.
Rectangular Coordinate System
A B
Similarly if the x–coordinate is
decreased by 4 to (2 – 4, 3)
= (–2, 3) – to the point C,
Hence we conclude that changes in the x–coordinates
correspond to moving the point right and left.
C
x–coord.
increased
by 4
x–coord.
decreased
by 4
(2, 3) (6, 3)(–2, 3)
this corresponds to moving A to the left by 4.

30. Let A be the point (2, 3).
Suppose its x–coordinate is
increased by 4 to (2 + 4, 3)
= (6, 3) – to the point B,
this corresponds to
moving A to the right by 4.
Rectangular Coordinate System
A B
Similarly if the x–coordinate is
decreased by 4 to (2 – 4, 3)
= (–2, 3) – to the point C,
Hence we conclude that changes in the x–coordinates
correspond to moving the point right and left.
If the x–change is +, the point moves to the right.
If the x–change is – , the point moves to the left.
C
x–coord.
increased
by 4
x–coord.
decreased
by 4
(2, 3) (6, 3)(–2, 3)
this corresponds to moving A to the left by 4.

31. Again let A be the point (2, 3).
Rectangular Coordinate System
A
(2, 3)

32. Again let A be the point (2, 3).
If the y–coordinate is
increased by 4 to (2, 3 + 4)
= (2, 7) – to the point D,
this corresponds to
moving A up by 4.
Rectangular Coordinate System
A
Dy–coord.
increased
by 4
(2, 3)
(2, 7)

33. Again let A be the point (2, 3).
If the y–coordinate is
increased by 4 to (2, 3 + 4)
= (2, 7) – to the point D,
this corresponds to
moving A up by 4.
Rectangular Coordinate System
A
D
If the y–coordinate is
decreased by 4 to (2, 3 – 4)
= (2, –1) – to the point E,
E
y–coord.
increased
by 4
y–coord.
decreased
by 4
(2, 3)
(2, 7)
(2, –1)
this corresponds to moving A down by 4.

34. Again let A be the point (2, 3).
If the y–coordinate is
increased by 4 to (2, 3 + 4)
= (2, 7) – to the point D,
this corresponds to
moving A up by 4.
Rectangular Coordinate System
A
D
If the y–coordinate is
decreased by 4 to (2, 3 – 4)
= (2, –1) – to the point E,
Hence we conclude that changes in the y–coordinates
correspond to moving the point up and down.
E
y–coord.
increased
by 4
y–coord.
decreased
by 4
(2, 3)
(2, 7)
(2, –1)
this corresponds to moving A down by 4.

35. Again let A be the point (2, 3).
If the y–coordinate is
increased by 4 to (2, 3 + 4)
= (2, 7) – to the point D,
this corresponds to
moving A up by 4.
Rectangular Coordinate System
A
D
If the y–coordinate is
decreased by 4 to (2, 3 – 4)
= (2, –1) – to the point E,
Hence we conclude that changes in the y–coordinates
correspond to moving the point up and down.
If the y–change is +, the point moves up.
If the y–change is – , the point moves down.
E
y–coord.
increased
by 4
y–coord.
decreased
by 4
(2, 3)
(2, 7)
(2, –1)
this corresponds to moving A down by 4.

36. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them,
The Distance Formula

37. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them,
DD
The Distance Formula
(2, –4)
(–1, 3)

38. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them,
Example A. Find the distance
between (–1, 3) and (2, –4).
DD
The Distance Formula
(2, –4)
(–1, 3)

39. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them, then D2 = Δx2 + Δy2,
where Δx = difference in the x's = x2 – x1,
Δy = difference in the y's = y2 – y1,
Example A. Find the distance
between (–1, 3) and (2, –4).
DD
The Distance Formula
(2, –4)
(–1, 3)

40. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them, then D2 = Δx2 + Δy2,
where Δx = difference in the x's = x2 – x1,
Δy = difference in the y's = y2 – y1,
Example A. Find the distance
between (–1, 3) and (2, –4).
(–1, 3)
– ( 2, –4)
DD
The Distance Formula
(2, –4)
(–1, 3)

41. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them, then D2 = Δx2 + Δy2,
where Δx = difference in the x's = x2 – x1,
Δy = difference in the y's = y2 – y1,
Example A. Find the distance
between (–1, 3) and (2, –4).
(–1, 3)
– ( 2, –4)
–3, 7
DD
The Distance Formula
(2, –4)
(–1, 3)
Δx Δy

42. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them, then D2 = Δx2 + Δy2,
where Δx = difference in the x's = x2 – x1,
Δy = difference in the y's = y2 – y1,
Example A. Find the distance
between (–1, 3) and (2, –4).
(–1, 3)
– ( 2, –4)
–3, 7
DD
7
-3
The Distance Formula
(2, –4)
(–1, 3)
Δx Δy

43. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them, then D2 = Δx2 + Δy2,
where Δx = difference in the x's = x2 – x1,
Δy = difference in the y's = y2 – y1,
Example A. Find the distance
between (–1, 3) and (2, –4).
(–1, 3)
– ( 2, –4)
–3, 7
D = (–3)2 + 72
DD
7
-3
The Distance Formula
(2, –4)
(–1, 3)
Δx Δy

44. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them, then D2 = Δx2 + Δy2,
where Δx = difference in the x's = x2 – x1,
Δy = difference in the y's = y2 – y1,
Example A. Find the distance
between (–1, 3) and (2, –4).
(–1, 3)
– ( 2, –4)
–3, 7
D = (–3)2 + 72
= 58  7.62
DD
7
-3
The Distance Formula
(2, –4)
(–1, 3)
Δx Δy

45. Let (x1, y1) and (x2, y2) be two points and
D = the distance between them, then D2 = Δx2 + Δy2,
where Δx = difference in the x's = x2 – x1,
Δy = difference in the y's = y2 – y1,
Hence D = Δx2 + Δy2
or
D = (x2 – x1)2+(y2 – y1)2
Example A. Find the distance
between (–1, 3) and (2, –4).
(–1, 3)
– ( 2, –4)
–3, 7
D = (–3)2 + 72
= 58  7.62
DD
7
-3
The Distance Formula
(2, –4)
(–1, 3)
Δx Δy

46. The Mid-Point Formula
The mid-point m between two numbers a and b is the
average of them, that is m = .a + b
2

47. The Mid-Point Formula
The mid-point m between two numbers a and b is the
average of them, that is m = .a + b
2
For example, the mid-point of 2 and 4 is (2 + 4)/2 = 3.

48. The Mid-Point Formula
The mid-point m between two numbers a and b is the
average of them, that is m = .a + b
2
For example, the mid-point of 2 and 4 is (2 + 4)/2 = 3.
In picture: a b(a+b)/2
mid-pt.

49. The Mid-Point Formula
The mid-point m between two numbers a and b is the
average of them, that is m = .a + b
2
For example, the mid-point of 2 and 4 is (2 + 4)/2 = 3.
In picture: a b(a+b)/2
mid-pt.
The mid-point formula
extends to higher
dimensions.

50. The Mid-Point Formula
The mid-point m between two numbers a and b is the
average of them, that is m = .a + b
2
For example, the mid-point of 2 and 4 is (2 + 4)/2 = 3.
In picture: a b(a+b)/2
mid-pt.
The mid-point formula
extends to higher
dimensions.
In 2D
(x1, y1)
(x2, y2)
x1
y1
y2
x2

51. The Mid-Point Formula
The mid-point m between two numbers a and b is the
average of them, that is m = .a + b
2
For example, the mid-point of 2 and 4 is (2 + 4)/2 = 3.
In picture: a b(a+b)/2
mid-pt.
The mid-point formula
extends to higher
dimensions.
In the x&y coordinate
the mid-point of
(x1, y1) and (x2, y2) is
x1 + x2
2 ,(
y1 + y2
2
)
In 2D
(x1, y1)
(x2, y2)
x1
y1
y2
x2

52. The Mid-Point Formula
The mid-point m between two numbers a and b is the
average of them, that is m = .a + b
2
For example, the mid-point of 2 and 4 is (2 + 4)/2 = 3.
In picture: a b(a+b)/2
mid-pt.
The mid-point formula
extends to higher
dimensions.
In the x&y coordinate
the mid-point of
(x1, y1) and (x2, y2) is
x1 + x2
2 ,(
y1 + y2
2
)
In 2D
(x1, y1)
(x2, y2)
x1
y1
y2
x2
(x1 + x2)/2
(y1 + y2)/2

53. A. Find the coordinates of the following points.
Sketch both points for each problem.
Rectangular Coordinate System
1. Point A that is 3 units to the left and 6 units down
from (–2, 5).
2. Point A that is 1 unit to the right and 5 units up
from (–3, 1).
3. a. Point B is 3 units to the left and 6 units up from
point A(–8, 4). Find the coordinate of point B.
b. Point A(–8, 4) is 3 units to the left and 6 units up from
point C, find the coordinate of point C
4. a. Point A is 37 units to the right and 63 units down from
point B(–38, 49), find the coordinate of point A.
b. Point A(–38, 49) is 37 units to the right and 63 units down
from point C, find the coordinate of point C.

54. 1. x – y = 3 2. 2x = 6 3. –y – 7= 0
4. y = 8 – 2x 5. y = –x + 4 6. 2x – 3 = 6
7. 2 = 6 – 2y 8. 4y – 12 = 3x 9. 2x + 3y = 0
10. –6 = 3x – 2y 11.
B. Graph the following equations by doing the following steps:
i. graph the horizontal lines (x = #) and
vertical lines (y = #) by inspection.
ii. identify which tilted lines may be graphed
using the x&y intercepts by completing the table:
iii. graph the other tilted lines passing
thru the origin using the following table:
3x = 4y 12. 5x + 2y = –10
Linear Equations and Lines
13. 3(2 – x) = 3x – y 14. 3(y – x) + y = 4y + 1
15. 5(x + 2) – 2y = 10

55. Linear Equations and Lines
C. Find the coordinates of the following points assuming
all points are evenly spaced.
1.
1 4
2.
–1 5
1 3 11
3. a. Find x and y.
x zy
The number z is a “weighted average” of {1, 3, 11}
whose average is 5. In this case z is the average of
{1, 3, 3,11} instead because “3” is used both for
calculating x and y.
1 3 11
b. Find z the mid-point of x and y.
x y
Find all the locations of the points in the figures.
(–4, 7)
(2, 3) (0, 0) (8, 0)
(2, 6)4. 5.

56. (Answers to odd problems) Exercise A.
1. B=(-5,-1) 3. B=(-11,10), C=(-5,-2)
Rectangular Coordinate System

57. 1. x – y = 3 3. –y – 7= 0 5. y = –x + 4
Exercise B.
x y
0 -3
3 0
x y
0 4
4 0y=7
Linear Equations and Lines

58. 7. 2 = 6 – 2y 9. 2x + 3y = 0 11. 3x = 4y
x y
0 0
1 -2/3
x y
0 0
1 3/4
y=4
Linear Equations and Lines

59. x y
0 -6
1 0
x y
0 0
1 5/2
13. 3(2 – x) = 3x – y 15. 5(x + 2) – 2y = 10
Linear Equations and Lines

60. Exercise C.
1.
1 4
1 3 11
3. a.
2 4.57
1 3 11
b.
2 7
1.75 2.5 3.25
(0, 0) (8, 0)
(2, 6)5.
(4, 0)
(1, 3)
(6, 6)
(10, 6)
(9, 3)
(5, 3)
(3.5, 4.5) (7.5, 4.5)
(6.5, 1.5)(2.5, 1.5)
Linear Equations and Lines