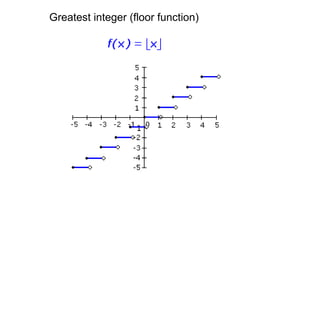
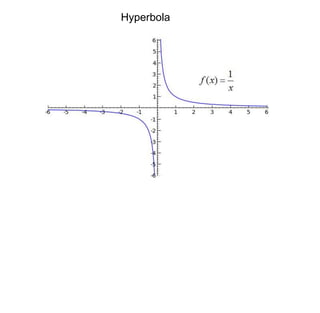
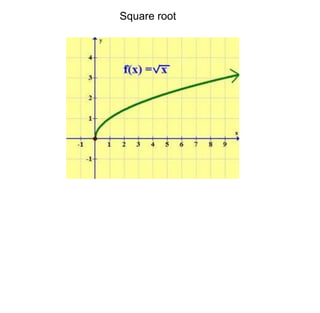
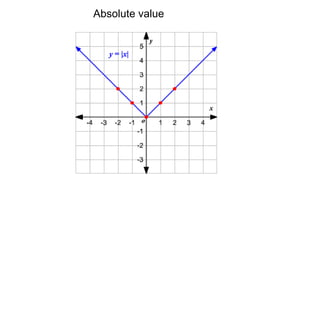
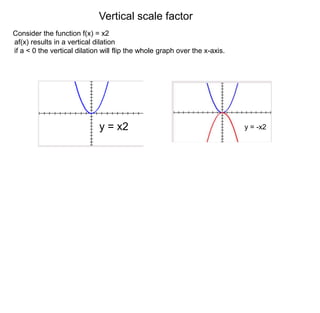
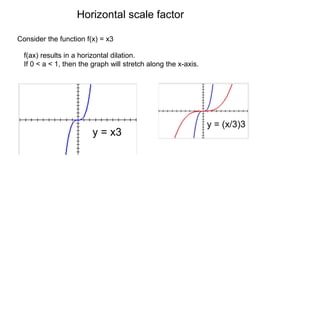
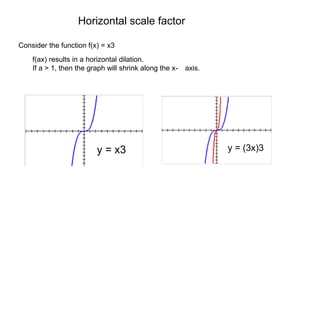
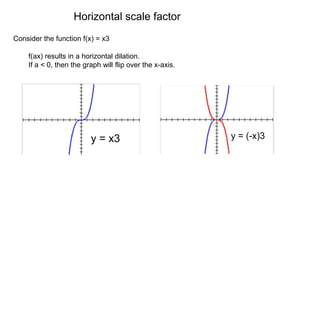
This document summarizes key concepts about transformations and graphs in statistics:
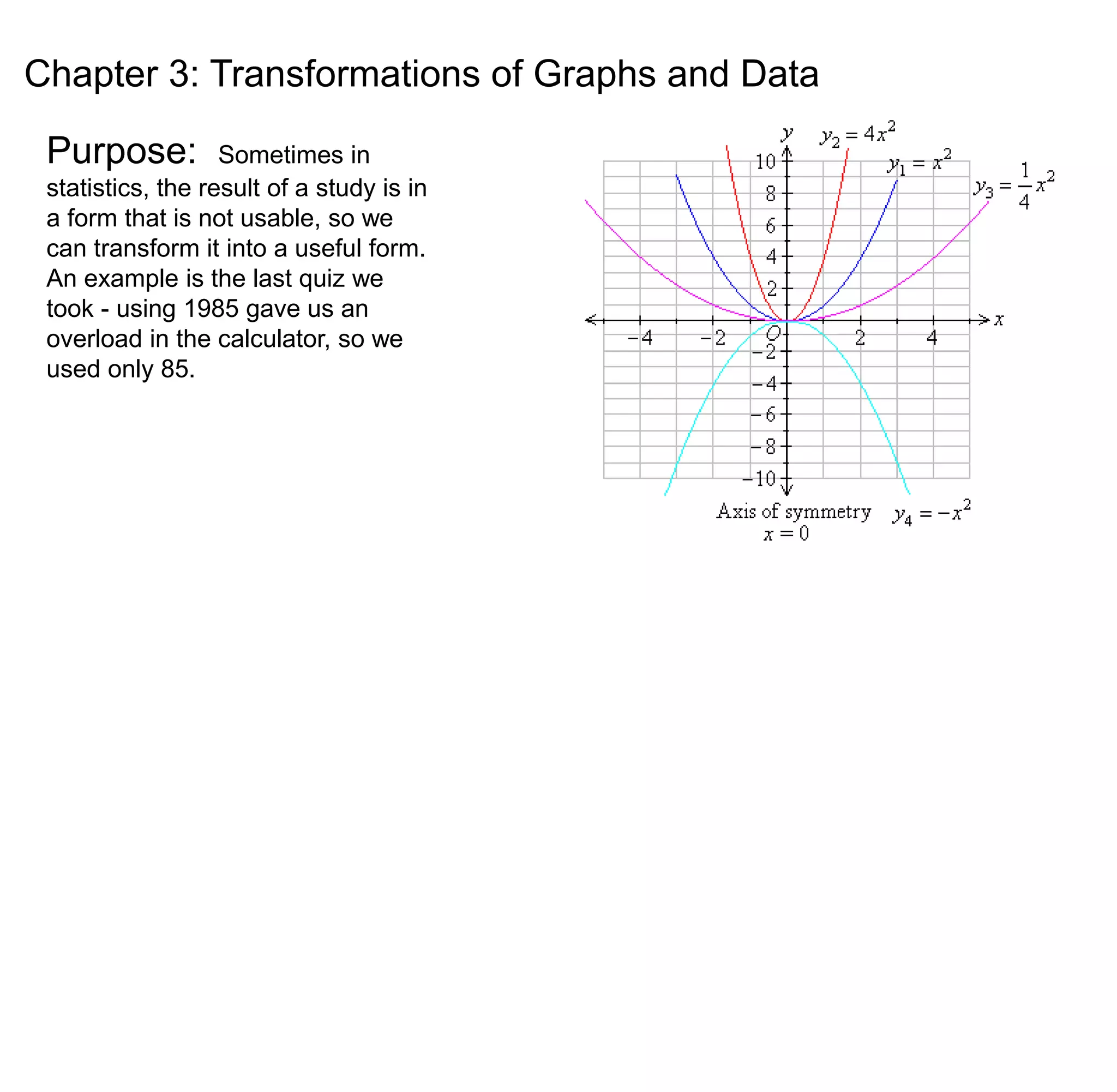
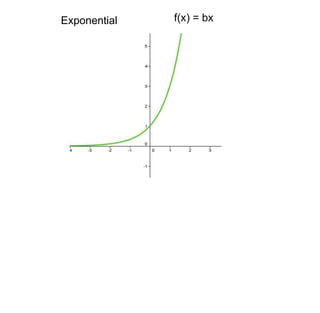
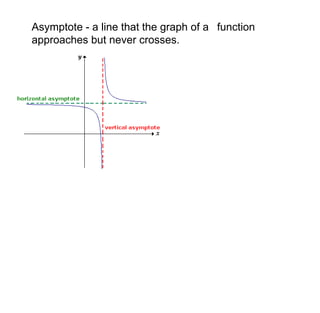
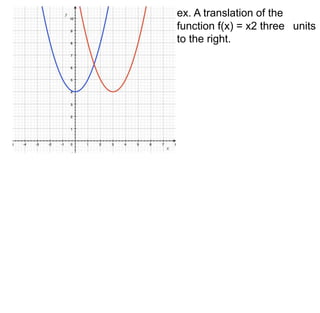
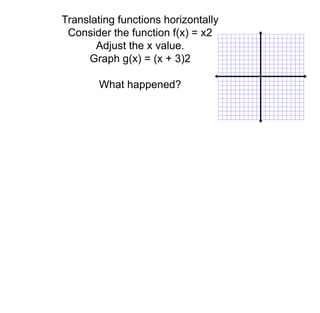
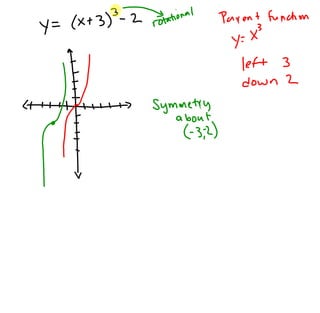
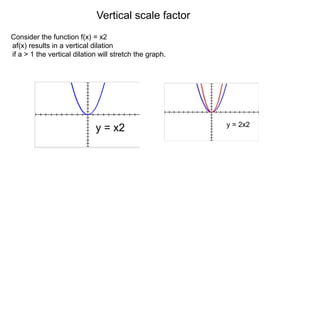
1) Transformations like translations, scale changes, and symmetries can be used to adjust graphs into more useful forms for analysis. Translations move a graph along the x- or y-axis, while scale changes dilate a graph vertically or horizontally.
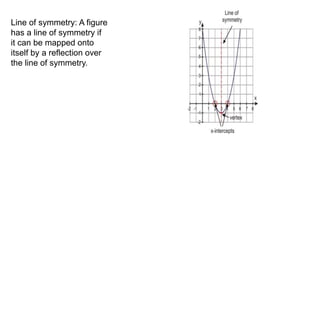
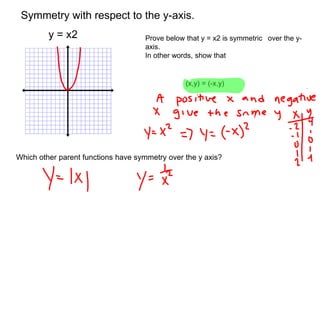
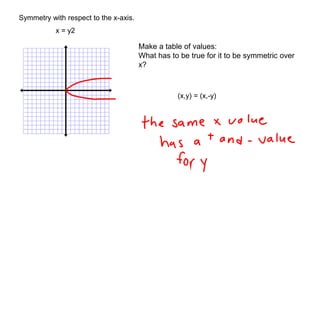
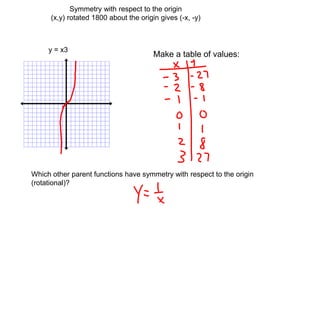
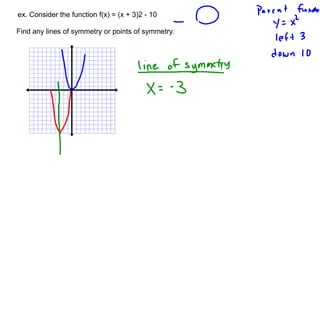
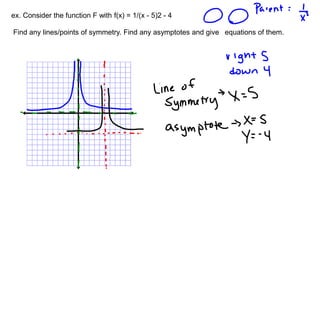
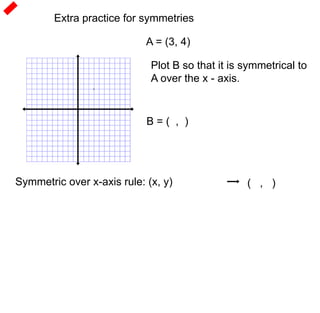
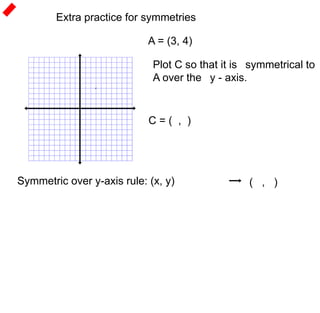
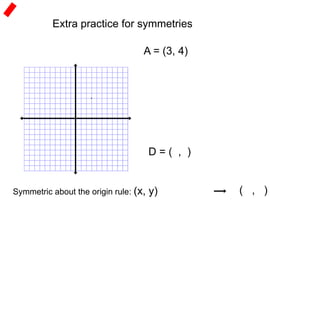
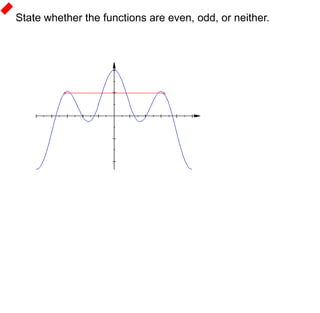
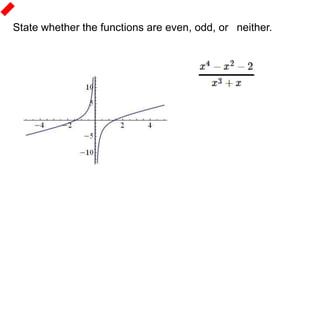
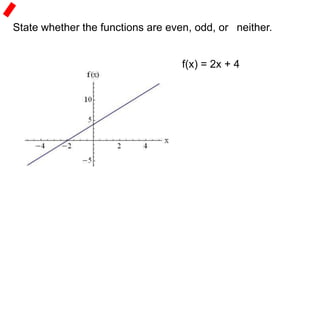
2) Symmetries include reflections like lines of symmetry and rotational symmetry about the origin. Even functions are symmetrical about the y-axis, while odd functions are symmetrical about the origin.
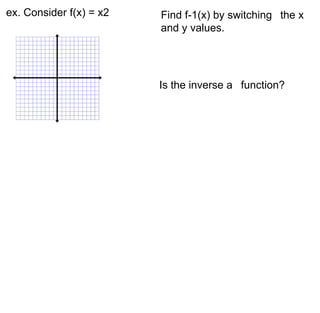
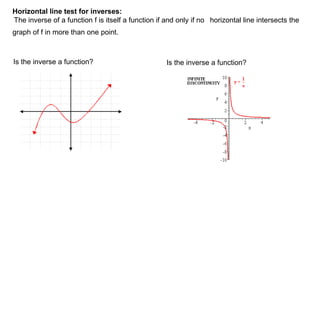
3) Inverse functions can be found by reflecting a function across the line y=x. The inverse of a function is a function itself if no horizontal line intersects the original function in more than