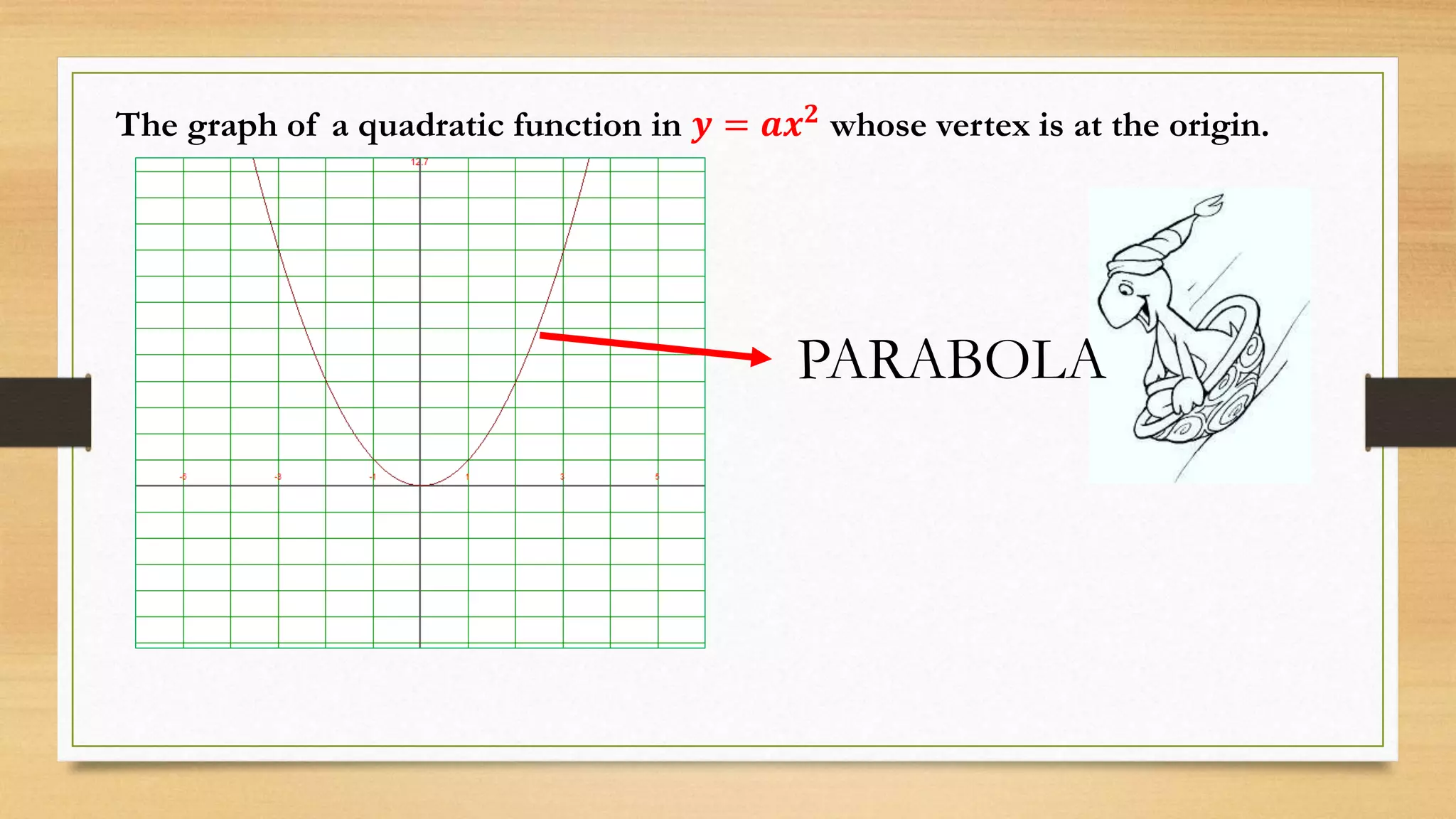
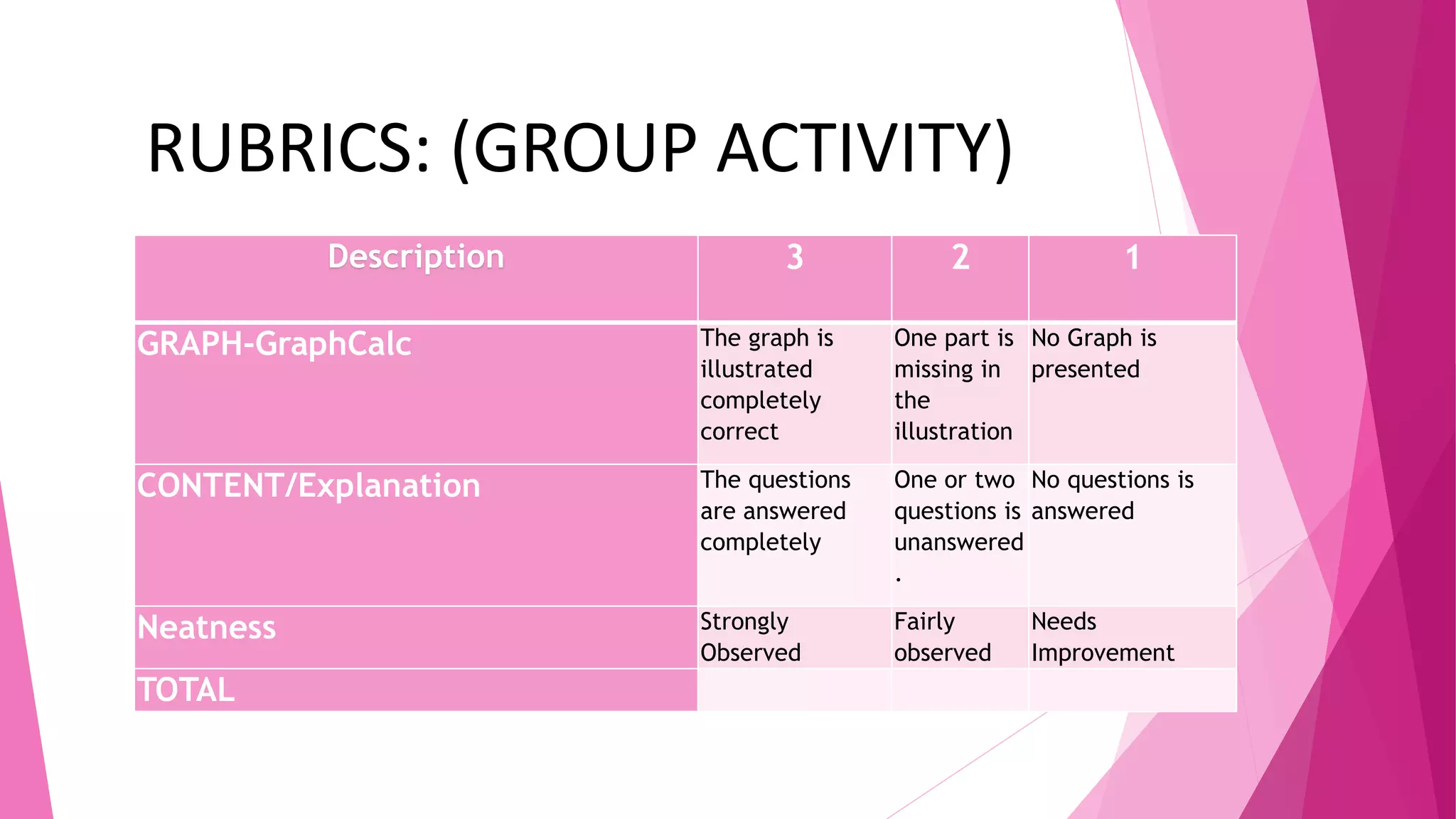
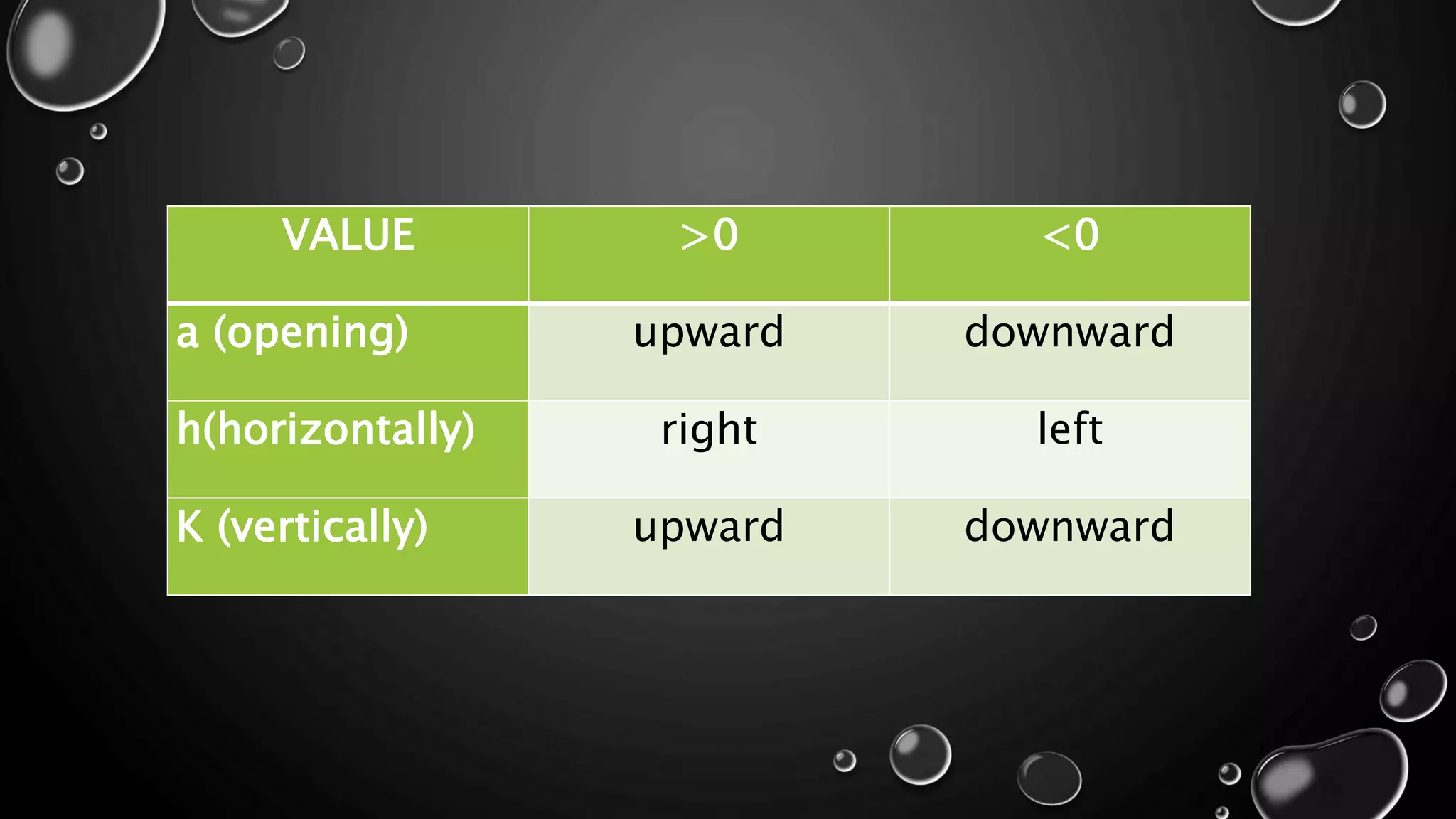
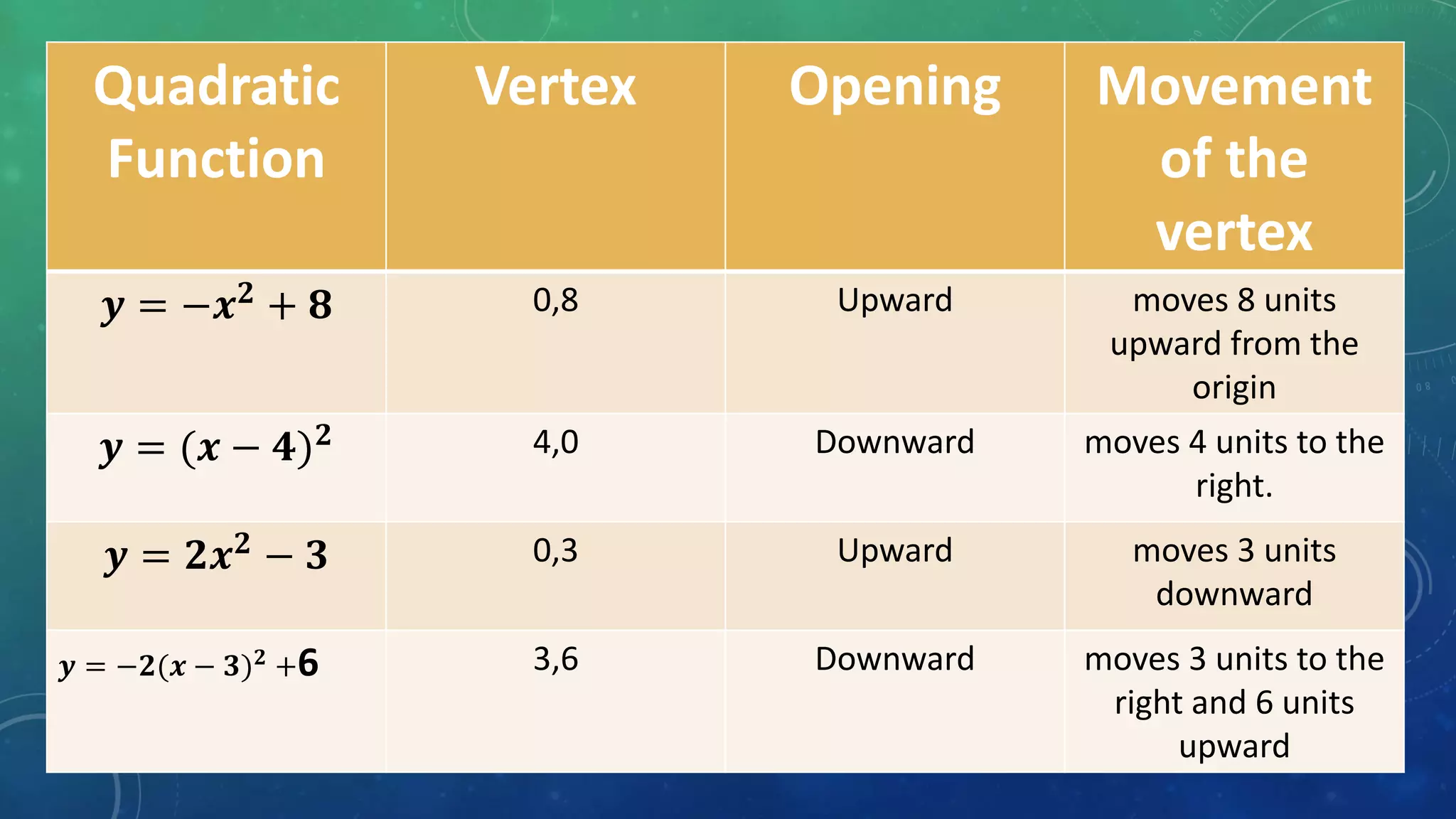
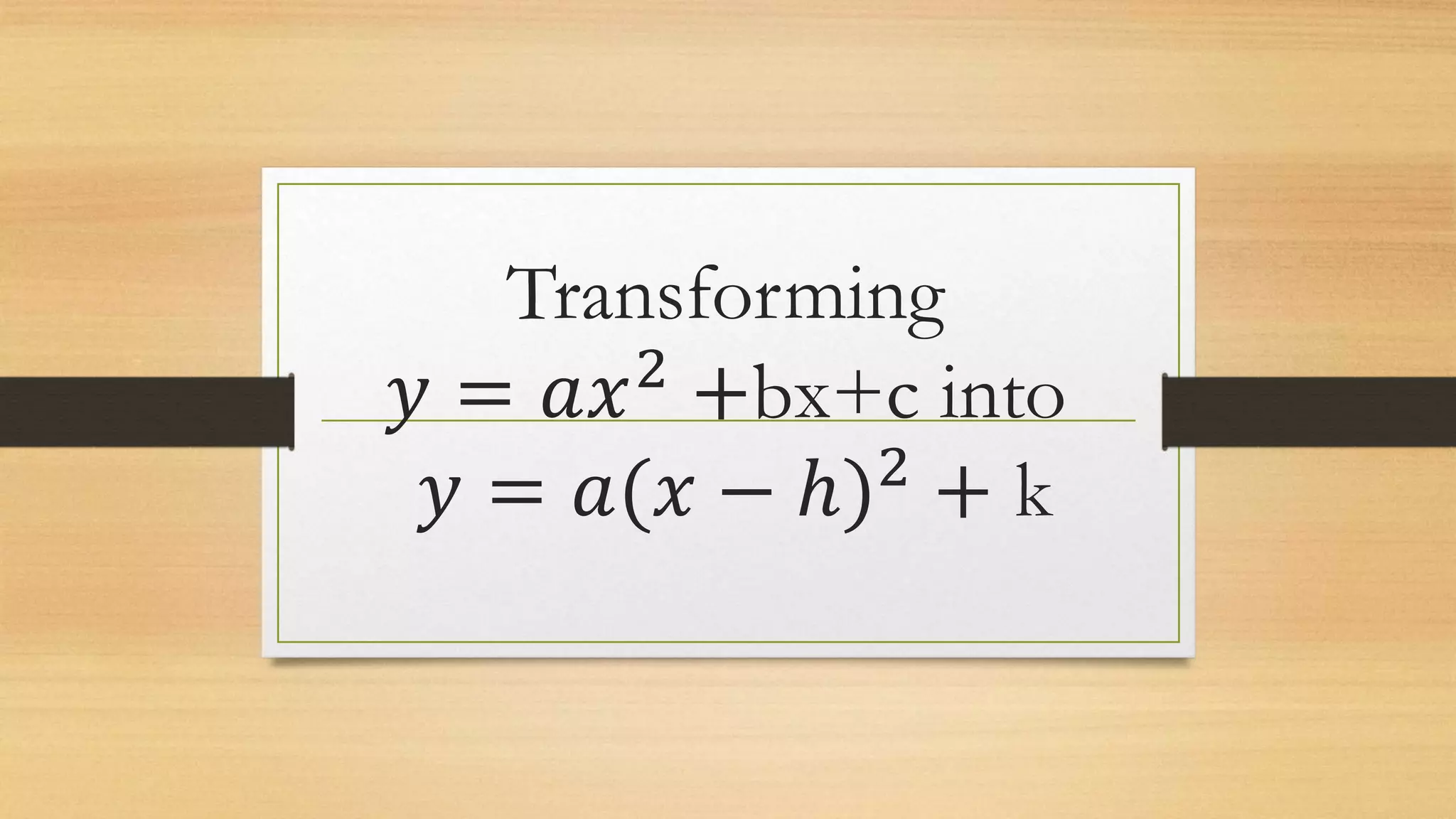The document discusses transforming quadratic functions into vertex form and describes how changing the values of a, h, and k affects the graph of the function. It then has students work in groups to graph and describe quadratic functions based on given equations in order to understand how the vertex, opening direction, and any shifts in the vertex position are represented algebraically.

1. Let’s
PRAY…

2. Transforming
𝑦 = 𝑎𝑥2
+bx+c into
𝑦 = 𝑎(𝑥 − ℎ)2
+ k

3. From 𝑦 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐,
We can transform them by means of
Completing the square or by h, k formula.
We arrived at 𝑦 = 𝑎(𝑥 − ℎ)2
+ 𝑘
Where h,k is the vertex.

4. Supposed that our vertex is at the Origin (0,0),
what would be our equation?
𝑦 = 𝑎(𝑥 − ℎ)2
+ 𝑘(h.k) = (0,0)
𝑦 = 𝑎(𝑥 − 0)2 + 0
𝑦 = 𝑎𝑥2

5. The graph of a quadratic function in 𝒚 = 𝒂𝒙 𝟐 whose vertex is at the origin.
PARABOLA

6. GROUP ACTIVITY

7. Using the Graph Calc.
Follow the direction given to
your group, and answer the
guide questions.

8. Description 3 2 1
GRAPH-GraphCalc The graph is
illustrated
completely
correct
One part is
missing in
the
illustration
No Graph is
presented
CONTENT/Explanation The questions
are answered
completely
One or two
questions is
unanswered
.
No questions is
answered
Neatness Strongly
Observed
Fairly
observed
Needs
Improvement
TOTAL
RUBRICS: (GROUP ACTIVITY)

9. How would you describe the opening of the
graph of a quadratic function as the value of
“a” becomes larger/smaller?
How do the value of “a”
affects the opening of the
graph?
How would you compare the
movement of the vertex of the
graph of y=ax2 to y=a(x-h)2 and
y=ax2+k?

10. As the value of “a” becomes larger the
opening of the graph becomes narrower,
and as the value of “a” becomes smaller its
opening becomes wider.If the value of a>0, it opens upward and if
a<0 it opens downward.
The graph of y=a(x-h)2, whose vertex is (h,0) if
h>0 the vertex slides h units to the right, and if
h <0, it slides h units to the left.The graph of y=ax2+k, whose vertex is
(0,k) if k>0 the vertex slides k units to the
upward, and if k<0, it slides k units to the
downward.The graph of y=(a-h)2+k,slide the graph of
y=ax2 moves h units horizontally and
vertically k units.

11. VALUE >0 <0
a (opening) upward downward
h(horizontally) right left
K (vertically) upward downward

12. Graph me..
Describe me…

13. QUADRATIC FUNCTION 1
QUADRATIC FUNCTION 2
QUADRATIC FUNCTION 3
QUADRATIC FUNCTION 4

14. Given the following quadratic functions. Describe its graph.
In terms of the following: Vertex, Opening and the
movement of the vertex.
QUADRATIC FUNCTION VERTEX OPENING MOVEMENT OF THE
VERTEX
𝒚 = −𝒙 𝟐 + 𝟖
𝒚 = (𝒙 − 𝟒) 𝟐
𝒚 = 𝟐𝒙 𝟐 − 𝟑
𝒚 = −𝟐(𝒙 − 𝟑) 𝟐
+6

15. Quadratic
Function
Vertex Opening Movement
of the
vertex
𝒚 = −𝒙 𝟐 + 𝟖 0,8 Upward moves 8 units
upward from the
origin
𝒚 = (𝒙 − 𝟒) 𝟐 4,0 Downward moves 4 units to the
right.
𝒚 = 𝟐𝒙 𝟐
− 𝟑 0,3 Upward moves 3 units
downward
𝒚 = −𝟐(𝒙 − 𝟑) 𝟐 +6 3,6 Downward moves 3 units to the
right and 6 units
upward

16. ASSIGNMENT:
(Notebook)
Given the graph of a quadratic
function, how would you
determine the equation?
Ref: LM in Math 9 page 156-168

19. DANCE