Embed presentation
Downloaded 312 times

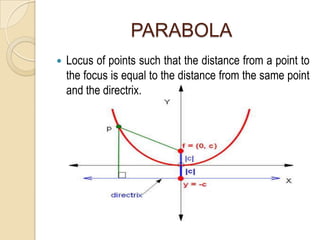

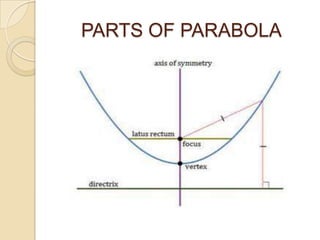
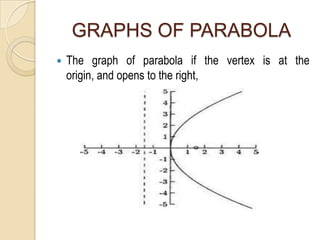
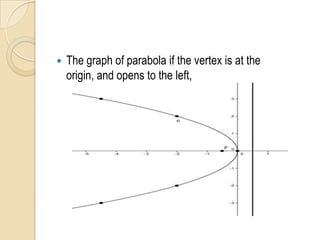
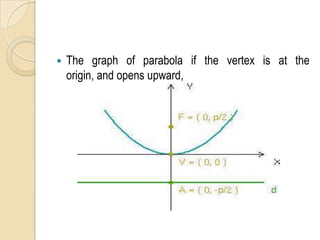
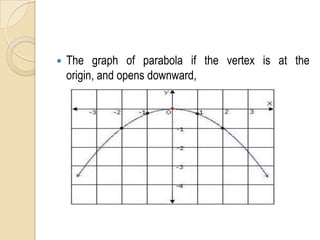

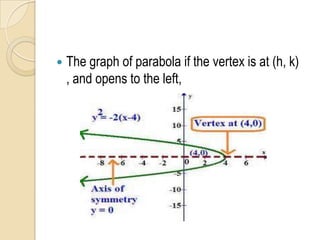
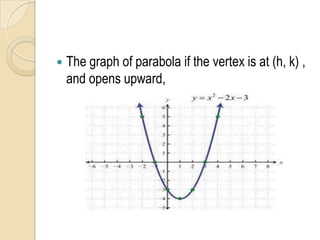
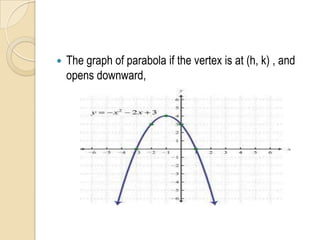

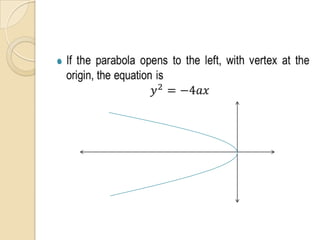
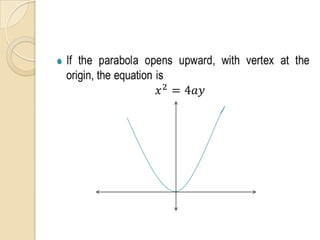
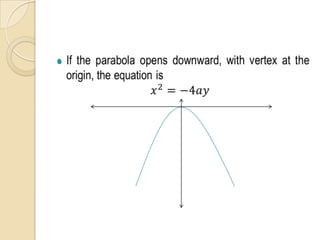
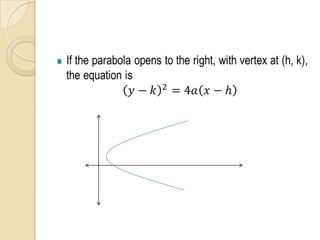
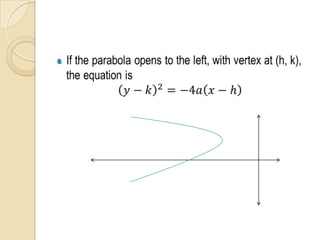
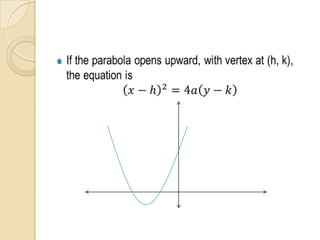
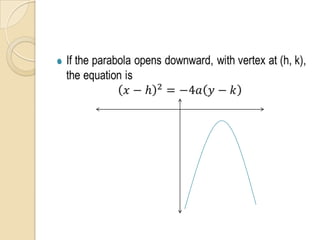





The document discusses parabolas including their parts, graphs, and equations. It defines a parabola as the locus of points where the distance to the focus is equal to the distance to the directrix. The parts of a parabola include the vertex, focus, directrix, axis of symmetry, and latus rectum. The document outlines the graphs of parabolas with the vertex at the origin or at a point (h,k), and opening in different directions. It notes equations will be provided for parabolas with the vertex at the origin or (h,k), but does not show the actual equations.























