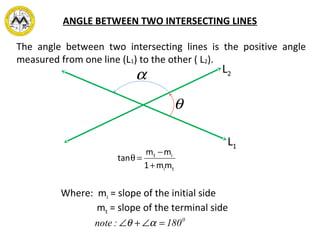
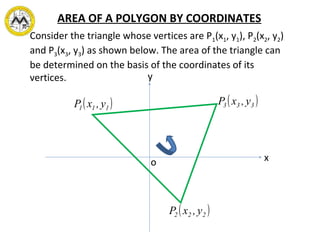
The document covers fundamental concepts of analytic geometry, including coordinate systems, distance formulas, and methods for solving problems involving lines, polygons, and equations of loci. It details various lessons on the properties of lines, slopes, divisions of line segments, and the equations representing geometric figures. Sample problems accompanying each lesson illustrate the application of these concepts in practical scenarios.

1. CALCULUS I( with Analytic Geometry)
MATH 21-1

2. CO2
Discuss comprehensively the fundamental
concepts in Analytic Geometry and use them to
solve application problems and problems
involving lines.

3. FUNDAMENTAL CONCEPTS OF ANALYTIC
GEOMETRY

4. Lesson 1: Rectangular Coordinate System,
Directed Distance, Distance Formula

5. OBJECTIVE:
At the end of the lesson, the students should be able to
illustrate properly and solve application problems involving
distance formula.

6. • Analytic Geometry – is the branch of mathematics, which
deals with the properties, behaviours, and solution of points,
lines, curves, angles, surfaces and solids by means of algebraic
methods in relation to a coordinate system(Quirino and
Mijares) .
• It is a unified algebra and geometry dealing with the study of
relationships between different geometric figures and
equations by means of the geometric properties and
processes of algebra in relation to a coordinate system
( Marquez, et al).
DEFINITION:
FUNDAMENTAL CONCEPTS

7. Two Parts of Analytic Geometry
1. Plane Analytic Geometry – deals with figures on a
plane surface (two-dimensional geometry, 2D).
2. Solid Analytic Geometry – deals with solid figures
( three-dimensional geometry, 3D).

8. Directed Line – a line in which one direction is chosen as
positive and the opposite direction as negative.
Directed Line Segment – portion of a line from one point
to another.
Directed Distance – the distance from one point to
another; may be positive or negative depending upon
which direction is denoted positive.
DEFINITION:

9. RECTANGULAR COORDINATES
A pair of number (x, y) in which x is the first and y the
second number is called an ordered pair. It defines the
position of a point on a plane by defining the directed
distances of the point from a vertical line and from a
horizontal line that meet at a point called the origin, O.
The x-coordinate of a point , known also as its abscissa, is
the directed distance of the point from the vertical axis, y-
axis; while the y-coordinate, also known as the ordinate, is
its directed distance from the horizontal axis, the x-axis.

10. DISTANCE BETWEEN TWO POINTS
The horizontal distance between any two points is the
difference between the abscissa (x-coordinate) of the
point on the right minus the abscissa (x-coordinate) of
the point on the left; that is,
Horizontal Distance Between Points
Distance, d= xright − xleft

11. Vertical Distance Between Any Two Points
The vertical distance between any two points is the
difference between the ordinate (y-coordinate) of the
upper point minus the ordinate (y-coordinate) of the
lower point; that is,
Distance d = yupper − ylower

12. Distance Between Any Two Points on a Plane
The distance between any two points on a plane
is the square root of the sum of the squares of
the difference of the abscissas and of the
difference of the ordinates of the points. That is,
if
distance d = x2 − x1( )
2
+ y2 − y1( )
2
P1 x1, y1( ) and P2 x2, y2( ) are the points, then

13. SAMPLE PROBLEMS
• By addition of line segments verify whether the points A ( - 3, 0 ) ,
B(-1, -1) and C(5, -4) lie on a straight line.
• The vertices of the base of an isosceles triangle are at (1, 2) and
(4, -1). Find the ordinate of the third vertex if its abscissa is 6.
3. Find the radius of a circle with center at (4, 1), if a chord of length 4
is bisected at (7, 4).
1. Show that the points A(-2, 6), B(5, 3), C(-1, -11) and D(-8, -8) are the
vertices of a rectangle.
2. The ordinate of a point P is twice the abscissa. This point is
equidistant from (-3, 1) and (8, -2). Find the coordinates of P.
6. Find the point on the y-axis that is equidistant from (6, 1) and (-2,
-3).

14. Lesson 2: DIVISION OF A LINE SEGMENT

15. OBJECTIVE:
At the end of the lesson, the students should be able to
illustrate properly and solve problems involving division of
line segments.

16. Let us consider a line segment bounded by the points
. This line segment can be subdivided
in some ratio and the point of division can be determined. It
is also possible to determine terminal point(s) whenever the
given line segment is extended beyond any of the given
endpoints or beyond both endpoints . If we consider the
point of division/ terminal point to be P (x, y ) and define
the ratio, r, to be
then the coordinates of point P are given by:
P1 x1, y1( ) and P2 x2, y2( )
r =
P1P
→
P1P2
→
x = x1 + r x2 − x1( )
y = y1 + r y2 − y1( )

17. If the line segment is divided into two equal parts, then the
point of division is called the midpoint. The ratio, r, is equal
to ½ and the coordinates of point P are given by:
or simply by:
x = x1 +
1
2
x2 − x1( )
y = y1 +
1
2
y2 − y1( )
x =
1
2
x1 + x2( )
y =
1
2
y1 + y2( )

18. SAMPLE PROBLEMS
•Find the midpoint of the segment joining (7, -2) and (-3, 5).
•The line segment joining (-5, -3) and (3, 4) is to be divided into five equal
parts. Find all points of division.
•The line segment from (1, 4) to (2, 1) is extended a distance equal to twice
its length. Find the terminal point.
•On the line joining (4, -5) to (-4, -2), find the point which is three-seventh the
distance from the first to the second point.
•Find the trisection points of the line joining (-6, 2) and (3, 8).
•What are the lengths of the segments into which the y-axis divided the
segment joining ( -6, -6) and (3, 6)?
•The line segment joining a vertex of a triangle and the midpoint of the
opposite side is called the median of the triangle. Given a triangle whose
vertices are A(4,-4), B(10, 4) and C(2, 6), find the point on each median that is
two-thirds of the distance from the vertex to the midpoint of the opposite
side.

19. Lesson 3: INCLINATION AND SLOPE A LINE

20. OBJECTIVES:
At the end of the lesson, the students should be able
to use the concept of angle of inclination and slope of a line
to solve application problems.

21. INCLINATION AND SLOPE OF A LINE
The angle of inclination of the line L or simply
inclination , denoted by , is defined as the smallest
positive angle measured from the positive direction of
the x-axis to the line.
The slope of the line, denoted by m , is defined
as the tangent of the angle of inclination; that is,
And if two points are points on
the line L then the slope m can be defined as
α
m = tanα
m = tanα =
y2 − y1
x2 − x1
P1 x1, y1( ) and P2 x2, y2( )

22. PARALLEL AND PERPENDICULAR LINES
If two lines are parallel their slope are
equal. If two lines are perpendicular, the slope of
one line is the negative reciprocal of the slope of
the other line.
If m1 is the slope of L1 and m2 is the slope
of L2 then , or
Sign Conventions:
Slope is positive (+), if the line is leaning to the right.
Slope is negative (-), if the line is leaning to the left.
Slope is zero (0), if the line is horizontal.
Slope is undefined , if the line is vertical.
m1m2 = −1.

23. x
y y
x
α1 α2
α2α1

24. SAMPLE PROBLEMS
1. Find the slope, m, and the angle of inclination of the
line through the points (8, -4) and (5, 9).
2. The line segment drawn from (x, 3) to (4, 1) is
perpendicular to the segment drawn from (-5, -6) to (4,
1). Find the value of x.
3. Find y if the slope of the line segment joining (3,
-2) to (4, y) is -3.

25. ANGLE BETWEEN TWO INTERSECTING LINES
θ
α
L1
L2
ti
it
mm1
mm
tan
+
−
=θ
Where: mi = slope of the initial side
mt = slope of the terminal side
The angle between two intersecting lines is the positive angle
measured from one line (L1) to the other ( L2).
0
180:note =∠+∠ αθ

26. Sample Problems
1.Find the angle from the line through the points (-1, 6)
and (5, -2) to the line through (4, -4) and (1, 7).
2.The angle from the line through (x, -1) and (-3, -5) to
the line through (2, -5) and (4, 1) is 450
. Find x
3.Two lines passing through (2, 3) make an angle of 450
with one another. If the slope of one of the lines is 2,
find the slope of the other.

27. AREA OF A POLYGON BY COORDINATES
Consider the triangle whose vertices are P1(x1, y1), P2(x2, y2)
and P3(x3, y3) as shown below. The area of the triangle can
be determined on the basis of the coordinates of its
vertices.
o
y
x
( )111 y,xP
( )222 y,xP
( )333 y,xP

28. Label the vertices counterclockwise and evaluate the area
of the triangle by:
1yx
1yx
1yx
2
1
A
33
22
11
=
The area is a directed area. Obtaining a negative value
will simply mean that the vertices were not named
counterclockwise. In general, the area of an n-sided
polygon can be determined by the formula :
1n54321
1n54321
yy..yyyyy
xx..xxxxx
2
1
A =

29. SAMPLE PROBLEMS
1. Find the area of the triangle whose vertices are (-
6, -4), (-1, 3) and (5, -3).
2.Find the area of a polygon whose vertices are (6,
-3), (3, 4), (-6, -2), (0, 5) and (-8, 1).

30. Lesson 4: EQUATION OF A LOCUS

31. OBJECTIVE:
At the end of the lesson, the students should be able to
determine the equation of a locus defining line, circle and
conics and other geometries defined by the given condition.

32. EQUATION OF A LOCUS
An equation involving the variables x and y is usually
satisfied by an infinite number of pairs of values of x and y,
and each pair of values corresponds to a point. These points
follow a pattern according to the given equation and form a
geometric figure called the locus of the equation.
Since an equation of a curve is a relationship satisfied
by the x and y coordinates of each point on the curve (but
by no other point), we need merely to consider an arbitrary
point (x,y) on the curve and give a description of the curve
in terms of x and y satisfying a given condition.

33. Sample Problems
Find an equation for the set of all points (x, y) satisfying
the given conditions.
1. It is equidistant from (5, 8) and (-2, 4).
2.The sum of its distances from (0, 4) and (0, -4) is 10.
3.It is equidistant from (-2, 4) and the y-axis

34. Lesson 5: STRAIGHT LINES / FIRST DEGREE
EQUATIONS

35. OBJECTIVE:
At the end of the lesson, the students is
should be able to write the equation of a line in the
general form or in any of the standard forms; as
well as, illustrate properly and solve application
problems concerning the normal form of the line.

36. STRAIGHT LINE
A straight line is the locus of a point that
moves in a plane in a constant slope.
Equation of Vertical/ Horizontal Line
If a straight line is parallel to the y-axis
( vertical line ), its equation is x = k, where k is
the directed distance of the line from the y-axis.
Similarly, if a line is parallel to the x-axis
( horizontal line ), its equation is y = k, where k is
the directed distance of the line from the x-axis.

37. General Equation of a Line
A line which is neither vertical nor horizontal
is defined by the general linear equation
Ax + By + C=0,
where A and B are nonzeroes.
The line has y-intercept of and slope of .−
C
B
−
A
B

38. DIFFERENT STANDARD FORMS OF THE
EQUATION OF A STRAIGHT LINE
A. POINT-SLOPE FORM:
If the line passes through the points ( x , y) and (x1, y1), then the
slope of the line is .
Rewriting the equation we have
which is the standard equation of the point-slope form.
1
1
xx
yy
m
−
−
=
( )11 xxmyy −=−

39. B. TWO-POINT FORM:
If a line passes through the points (x1, y1) and (x2, y2), then the
slope of the line is .
Substituting it in the point-slope formula will result to
the standard equation of the two-point form.
12
12
xx
yy
m
−
−
=
( )1
12
12
1 xx
xx
yy
yy −





−
−
=−

40. C. SLOPE-INTERCEPT FORM:
Consider a line containing the point P( x, y) and not parallel to
either of the coordinate axes. Let the slope of the line be m
and the y-intercept ( the intersection point with the y-axis) at
point (0, b), then the slope of the line is .
Rewriting the equation, we obtain
the standard equation of the slope-intercept form.
0x
by
m
−
−
=
bmxy +=

41. D. INTERCEPT FORM:
Let the intercepts of a line be the points (a, 0), the x-
intercept, and (0, b), the y-intercept. Then the slope of
the line is defined by .
Using the Point-slope form, the equation is written as
or simply as
the standard equation of the Intercept Form.
a
b
m −=
( )0x
a
b
by −−=−
1
b
y
a
x
=+

42. E. NORMAL FORM:
Suppose a line L, whose equation is to be found, has its
distance from the origin to be equal to p. Let the angle of
inclination of p be .
Since p is perpendicular to L, then the slope of p is equal to the
negative reciprocal of the slope of L,
Substituting in the slope-intercept form y = mx + b , we obtain
or
the normal form of the straight line
θ
θ
θ
θ
θ sin
cos
mor,cot
tan
1
m −=−=−=
θθ
θ
sin
p
x
sin
cos
y +−=
py sincosx =+ θθ

43. Reduction of the General Form to the Normal Form
The slope of the line Ax+By+C=0 is . The slope of p which is
perpendicular to the line is therefore ; thus, .
From Trigonometry, we obtain the values
and .
If we divide the general equation of the straight line by
, we have
or
This form is comparable to the normal form .
Note: The radical takes on the sign of B.
B
A
−
A
B
A
B
tan =θ
22
BA
B
sin
+±
=θ
22
BA
A
cos
+±
=θ
22
BA +± 0
BA
C
y
BA
B
x
BA
A
222222
=
+±
+
+±
+
+±
BA
C
y
BA
B
x
BA
A
222222
+±
−
=
+±
+
+±
py sincosx =+ θθ

44. PARALLEL AND PERPENDICULAR LINES
Given a line L whose equation is Ax + By + C = 0.
The line Ax + By + K = 0 , for any constant K not
equal to C, is parallel to L;
and the Bx – Ay + K = 0 is perpendicular to L.

45. DIRECTED DISTANCE FROM A LINE TO A POINT
The directed distance of the point P(x1, y1) from the
line Ax + By + C = 0 is ,
where the radical takes on the sign of B.
22
11
BA
CByAx
d
+±
++
=

46. y
x
•
•
( )111 y,xP
( )222 y,xP
0CByAx 11 =++
0d1 >
0d2 <
linethebelowis
pointthe0,dif
linetheaboveis
pointthe0,dif
:note
<•
>•

47. Sample Problems
1. Determine the equation of the line passing through (2, -3) and
parallel to the line through (4,1) and (-2,2).
2. Find the equation of the line passing through point (-2,3) and
perpendicular to the line 2x – 3y + 6 = 0
3. Find the equation of the line, which is the perpendicular bisector
of the segment connecting points (-1,-2) and (7,4).
4. Find the equation of the line whose slope is 4 and passing through
the point of intersection of lines x + 6y – 4 = 0 and 3x – 4y + 2 = 0.
5. The points A(0, 0), B(6, 0) and C(4, 4) are vertices of triangles. Find:
a. the equations of the medians and their intersection point

48. 6. Find the distance from the line 5x = 2y + 6 to the point (3, -5).
7. Find the equation of the bisector of the acute angles and also the
bisector of the obtuse angles formed by the lines x + 2y – 3 = 0 and 2x + y –
4 = 0.
8. Determine the distance between the lines: 2x + 5y -10 =0 ; 4x + 10y + 25
= 0.
9. Write the equation of the line a) parallel to b) perpendicular to 4x + 3y
-10 = 0 and is 3 units from the point ( 2, -1).

49. CLASSWORK 1
1. The abscissa and ordinate of a point units from (3, 3) are
numerically equal but of opposite signs. Find the point.
2.Given two points A(8, 6) and B(–7, 9), determine a third point P(x,
y) such that the slopes of AP and BP are ½ and –2/3 respectively.
3.A line through (–6,–7) and (x, 7) is perpendicular to a line through
(1,–4) and (–5, 2). Find x.
4.A line passes through (6,–4) and makes an angle of 1350
with the
x-axis. Find the equation of the line.
5.The angle from the line through (–1, y) and (4,–7) to the line
through (4, 2) and (–1,–9) is 1350
. Find y.
6.Find the equation of the bisector of the obtuse angle between
the lines x + 2y – 3 = 0 and 2x + y – 4 = 0.
52

50. REFERENCES
Analytic Geometry, 6th
Edition, by Douglas F. Riddle
Analytic Geometry, 7th
Edition, by Gordon Fuller/Dalton Tarwater
Analytic Geometry, by Quirino and Mijares
Fundamentals of Analytic Geometry by Marquez, et al.
Algebra and Trigonometry, 7th
ed by Aufmann, et al.