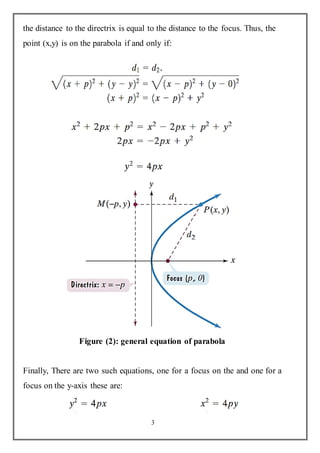
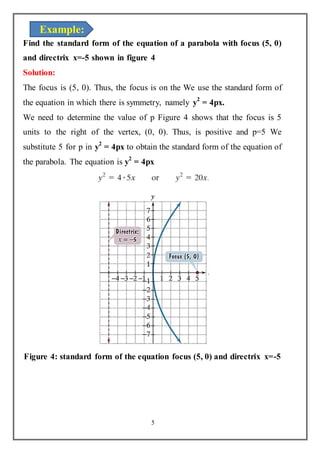
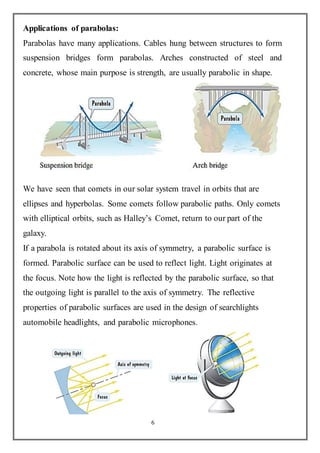
This document discusses parabolas and their key properties and applications. It begins by introducing parabolas as sets of points equidistant from a fixed line called the directrix and a fixed point called the focus. The standard form of a parabola equation is presented. Properties of parabolas including the vertex, axis of symmetry, focus, and directrix are described. Applications where parabolic shapes are used such as suspension bridges, vehicle headlights, and satellite dishes are also mentioned. Parabolas are widely used to model projectile motion and in optical systems where their reflective properties help focus or direct light.

1. PARABOLA

2. 1
Parabola
Introduction:
At first glance, this image looks like columns of smoke rising from a fire
into a starry sky. Those are, indeed, stars in the background, but you are
not looking at ordinary smoke columns. These stand almost 6 trillion miles
high and are 7000 light-years from Earth—more than 400 million times as
far away as the sun.
This NASA photograph is one of a series of stunning images captured
from the ends of the universe by the Hubble Space Telescope. The image
shows infant star systems the size of our solar system emerging from the
gas and dust that shrouded their creation. Using a parabolic mirror that is
94.5 inches in diameter, the Hubble has provided answers to many of the
profound mysteries of the cosmos: How big and how old is the universe?
How did the galaxies come to exist? Do other Earth-like planets orbit other
sun-like stars? In this section, we study parabolas and their applications,
including parabolic shapes that gather distant rays of light and focus them
into spectacular images.

3. 2
Parabola definition:
A parabola is the set of all points in a plane that are equidistant from a
fixed line, the directrix, and a fixed point, the focus, that is not on the line
(seeFigure1).
Parabolas can be given a geometric definition that enables us to include
graphs that open to the left or to the right, as well as those that open
obliquely. The definitions of ellipses and hyperbolas involved two fixed
points, the foci. By contrast, the definition of a parabola is based on one
point and a line.
Figure (1): Parabola
Standard Form of the Equation of a Parabola:
The rectangular coordinate system enables us to translate a parabola’s
geometric definition into an algebraic equation. Figure 2 is our starting
point for obtaining an equation. We place the focus on the at the point The
directrix has an equation given by The vertex, located midway between the
focus and the directrix, is at the origin. What does the definition of a
parabola tell us about the point in Figure 2 for any point on the parabola,

4. 3
the distance to the directrix is equal to the distance to the focus. Thus, the
point (x,y) is on the parabola if and only if:
Figure (2): general equation of parabola
Finally, There are two such equations, one for a focus on the and one for a
focus on the y-axis these are:

5. 4
Finding the Focus and Directrix of a Parabola:
Find the focus and directrix of the parabola given by y2
= 12x Then
graph the parabola.
Solution:
The given equation y2
= 12x, is in the standard form y2
=4px, so 4p=12
We can find both the focus and the directrix by finding p.
Because p is positive, the parabola, with its x-axis symmetry, opens to the
right. The focus is 3 units to the right of the vertex, (0, 0).
The focus, (3, 0), and directrix, x=-3 are shown in Figure 3.
To graph the parabola, we will use two points on the graph that lie directly
above and below the focus. Because the focus is at (3, 0), substitute 3 for
in the parabola’s equation, y2
= 12x
The points on the parabola above and
below the focus are (3, 6) and (3,-6).
Figure3: graph of equation y2
= 12x
Example:

6. 5
Find the standard form of the equation of a parabola with focus (5, 0)
and directrix x=-5 shown in figure 4
Solution:
The focus is (5, 0). Thus, the focus is on the We use the standard form of
the equation in which there is symmetry, namely y2
= 4px.
We need to determine the value of p Figure 4 shows that the focus is 5
units to the right of the vertex, (0, 0). Thus, is positive and p=5 We
substitute 5 for p in y2
= 4px to obtain the standard form of the equation of
the parabola. The equation is y2
= 4px
Figure 4: standard form of the equation focus (5, 0) and directrix x=-5
Example:

7. 6
Applications of parabolas:
Parabolas have many applications. Cables hung between structures to form
suspension bridges form parabolas. Arches constructed of steel and
concrete, whose main purpose is strength, are usually parabolic in shape.
We have seen that comets in our solar system travel in orbits that are
ellipses and hyperbolas. Some comets follow parabolic paths. Only comets
with elliptical orbits, such as Halley’s Comet, return to our part of the
galaxy.
If a parabola is rotated about its axis of symmetry, a parabolic surface is
formed. Parabolic surface can be used to reflect light. Light originates at
the focus. Note how the light is reflected by the parabolic surface, so that
the outgoing light is parallel to the axis of symmetry. The reflective
properties of parabolic surfaces are used in the design of searchlights
automobile headlights, and parabolic microphones.

8. 7
Summary:
A parabola is a curve in mathematics that is shaped like an open bowl or
U. It is a type of conic section, formed by the intersection of a right
circular cone and a plane parallel to one of the cone's sides. The key
defining feature of a parabola is that it is symmetrical.
The standard form of a parabola equation is (y = ax2
+ bx + c), where (a),
(b), and (c) are constants, and (x) and (y) are variables. The sign of (a)
determines whether the parabola opens upwards (a > 0) or downwards
(a < 0). The vertex of the parabola, the point where it changes direction, is
given by the coordinates -b/2a, f(-b/2a)
Parabolas have several important properties:
1- Vertex: The vertex is the minimum or maximum point on the
parabola, depending on whether it opens upwards or downwards.
2- Axis of Symmetry: The line passing through the vertex and dividing
the parabola into two symmetrical halves is called the axis of
symmetry.
3- Focus and Directrix: A parabola can be defined geometrically using a
focus and directrix. All points on the parabola are equidistant from
the focus and the directrix.
4- Focal Length: The distance between the vertex and the focus (or the
vertex and the directrix) is called the focal length.
5- Standard Formulas:
- The distance between the vertex and the focus ((|FP|)) or the vertex
and the directrix (|PV|) is given by (|FP| = |PV| = 1 (4|a)
- The equation of the axis of symmetry is (x = -b/(2a)

9. 8
Parabolas are prevalent in various fields, including physics, engineering,
and computer science. They are commonly used to model the trajectories
of projectiles, such as the path of a thrown object. Additionally, parabolic
shapes are found in optical systems, satellite dishes, and other applications
where focusing or reflecting is essential.