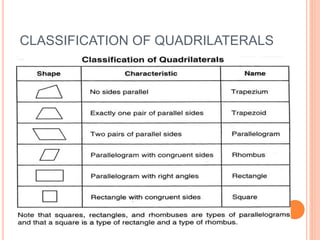
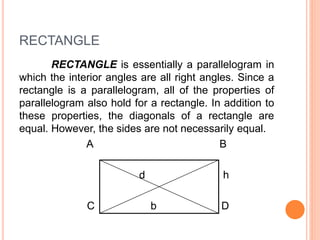
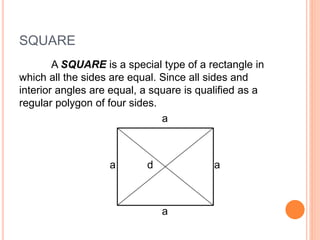
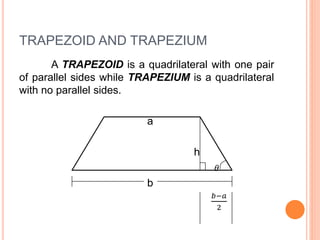
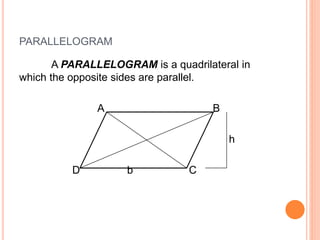
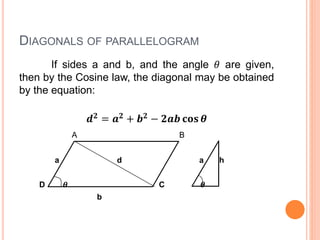
This document defines and describes the six types of quadrilaterals: square, rectangle, parallelogram, rhombus, trapezoid, and trapezium. It provides the key properties and formulas to calculate the perimeter, area, and diagonals of each shape. The main properties discussed include opposite sides being parallel, equal or congruent, interior angles being right angles or supplementary, and using formulas like the Pythagorean theorem, area equals base times height, and perimeter equals the sum of all sides.

1. QUADRILATERALS

2. QUADRILATERALS
QUADRILATERALS, known as TETRAGON
or QUADRANGLE, is a general term for a four-sided
polygon. There are six types of quadrilaterals: square,
rectangle, parallelogram, rhombus, trapezoid and
trapezium. Each type of quadrilateral has unique
properties that make it distinct from the other types.

3. PARTS OF A QUADRILATERAL
SIDE is a line segment which joins any two adjacent
vertices
INTERIOR ANGLE is the angle formed between two
adjacent sides
HEIGHT OR ALTITUDE is the distance between two
parallel sides of a quadrilateral
BASE is the side that is perpendicular to the altitude
DIAGONAL is the line segment joining any two non-
adjacent vertices

4. CLASSIFICATION OF QUADRILATERALS

5. RECTANGLE
RECTANGLE is essentially a parallelogram in
which the interior angles are all right angles. Since a
rectangle is a parallelogram, all of the properties of
parallelogram also hold for a rectangle. In addition to
these properties, the diagonals of a rectangle are
equal. However, the sides are not necessarily equal.
A B
d h
C b D

6. DIAGONALS OF A RECTANGLE
A diagonal of a rectangle cuts the rectangle into
two congruent right triangles. Since the diagonal of the
rectangle forms right triangles that include the diagonal
and two sides of the rectangle, one can always compute
for the third side with the use of the PYTHAGOREAN
THEOREM. Thus,
𝒅 = 𝒃 𝟐 + 𝒉 𝟐
Where d is the diagonal of the rectangle
b is the base of the rectangle
h is the height or the altitude of the rectangle

7. PERIMETER AND AREA OF A RECTANGLE
The perimeter is the sum of the four sides.
Thus,
𝑷 = 𝟐𝒃 + 𝟐𝒉 = 𝟐(𝒃 + 𝒉)
The formula to solve the area of the rectangle
is given by
𝑨 = 𝒃𝒉

8. SQUARE
A SQUARE is a special type of a rectangle in
which all the sides are equal. Since all sides and
interior angles are equal, a square is qualified as a
regular polygon of four sides.
a
a d a
a

9. DIAGONAL, PERIMETER AND AREA OF
A SQUARE
To find the diagonal, use
𝒅 = 𝒂 𝟐 + 𝒂 𝟐 = 𝟐𝒂 𝟐 = 𝒂 𝟐
To find the perimeter, use
𝑷 = 𝟒𝒂
To find the area, use
𝑨 = 𝒂 𝟐

10. RHOMBUS
A RHOMBUS is a parallelogram in which all
sides are equal. It is also defined as an equilateral
parallelogram. The terms “rhomb” or “diamond” are
sometimes used instead of rhombus. A rhombus with
an interior angle of 45 degrees is sometimes called a
“lozenge”.
𝒅 𝟏 𝒅 𝟐
𝜽
𝟐
h
𝜽
𝟐
b

11. DIAGONALS OF A RHOMBUS
The diagonals of the rhombus are angle bisectors
of the vertices. By the Cosine law, the diagonals may be
obtained in a similar manner like that of parallelogram.
Thus,
𝒅 𝟏
𝟐
= 𝟐𝒃 𝟐
𝟏 − 𝐜𝐨𝐬 𝜽
𝒅 𝟐
𝟐
= 𝟐𝒃 𝟐 𝟏 + 𝒄𝒐𝒔 𝜽
One can also verify that the angle opposite the
shorter diagonal 𝑑1, may be obtained by the formula
𝜽 = 𝟐 𝐭𝐚𝐧−𝟏
𝒅 𝟏
𝒅 𝟐

12. PERIMETER OF A RHOMBUS
If b is the measure of one side of a rhombus,
then the perimeter is given by
𝑷 = 𝟒𝒃

13. AREA OF A RHOMBUS
The area of a rhombus may be determined by
any of the following ways:
The area is one-half the product of its two diagonals,
thus, 𝑨 =
𝟏
𝟐
𝒅 𝟏 𝒅 𝟐
The area is also the product of the base and the
height, thus 𝑨 = 𝒃𝒉
The area is twice the area of one of the two
congruent triangles formed by one of its diagonals.
Thus, 𝑨 = 𝒃 𝟐 𝒔𝒊𝒏 𝜽

14. TRAPEZOID AND TRAPEZIUM
A TRAPEZOID is a quadrilateral with one pair
of parallel sides while TRAPEZIUM is a quadrilateral
with no parallel sides.
a
h
𝜃
b
𝑏−𝑎
2

15. AREA OF A TRAPEZOID
The area of a trapezoid is equal to the product
of the mean of the bases and the height. In symbols,
the are is given by the formula,
𝑨 =
𝟏
𝟐
𝒂 + 𝒃 𝒉
Hence, in finding the area of a trapezium, you
may use any of the three formulas for the area of a
quadrilateral.

16. PARALLELOGRAM
A PARALLELOGRAM is a quadrilateral in
which the opposite sides are parallel.
A B
h
D b C

17. IMPORTANT PROPERTIES OF
PARALLELOGRAM
 Opposite sides are equal.
 Opposite interior angles are congruent.
 Adjacent angles are supplementary.
 A diagonal divides the parallelogram into two
congruent triangles.
 The two diagonals bisect each other.

18. DIAGONALS OF PARALLELOGRAM
If sides a and b, and the angle 𝜃 are given,
then by the Cosine law, the diagonal may be obtained
by the equation:
𝒅 𝟐 = 𝒂 𝟐 + 𝒃 𝟐 − 𝟐𝒂𝒃 𝐜𝐨𝐬 𝜽
A B
a d a h
D 𝜽 C 𝜽
b

19. PERIMETER OF A PARALLELOGRAM
Opposite sides of a parallelogram are equal.
Thus, its perimeter is given by the equation,
𝑷 = 𝟐𝒂 + 𝟐𝒃 = 𝟐 𝒂 + 𝒃

20. AREA OF A PARALLELOGRAM
The area of a parallelogram, can be obtained
by any of the following formulas:
𝑨 = 𝒃𝒉
where b is the base and h is the height of the
parallelogram.
𝑨 = 𝒂𝒃 𝐬𝐢𝐧 𝜽
where a and b are the lengths of the sides of the
parallelogram and 𝜽 is the interior angle.

21. NOTE TO ES12KA3
1. Answer CHAPTER TEST pages 41 to 43 of
“SOLID MENSURATION:UNDERSTANDING THE
3D SPACE” by Richard T. Earnheart, latest edition
(green book)
2. Answers only. Use only short bond paper.
3. Deadline is until December 7, 2105. You may
submit your assessment (written recitation #1)
during our class.
4. Erasures are not allowed.