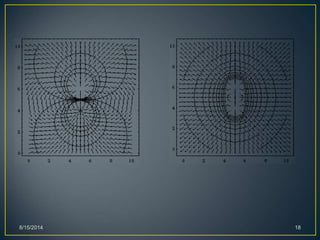
The document summarizes key concepts about electric potential and electric potential energy. It defines electric potential as the work required per unit charge to move a charge from a reference point to its current position in an electric field. Electric potential energy is defined as stored energy in a charge-field system due to the charges' positions. The document outlines how electric potential and potential energy relate to work, electric fields, and voltage. It also discusses applications of these concepts, including conductors, equipotential surfaces, and the Bohr model of the hydrogen atom.

1. 8/15/2014 1

2. • When a test charge is placed in an electric field, it
experiences a force.
𝑭 = 𝒒𝑬 (𝒕𝒉𝒆 𝒇𝒐𝒓𝒄𝒆 𝒊𝒔 𝒄𝒐𝒏𝒔𝒆𝒓𝒗𝒂𝒕𝒊𝒗𝒆)
• If the test charge is moved in the field by some external
agent, the work done by the field is the negative of the
work done by the external agent.
• 𝒅𝒔 is an infinitesimal displacement vector that is oriented
tangent to a path through space. The path may be
straight or curved and the integral performed along this
path is called either a path integral or line integral
8/15/2014 2

3. • The work done within the charge-field system by the electric
field on the charge is
𝑾 = 𝑭 ∙ 𝒅𝒔 = 𝒒𝑬 ∙ 𝒅𝒔
• At this, work is done by the field, the potential energy of the
charge-field system is changed by
𝑾 = −𝒒 𝟎 𝑬 ∙ 𝒅𝒔 = ∆𝑼
• For a finite displacement of the charge from A to B, the change
in potential energy of the system is
∆𝑼 = 𝑼 𝑨 − 𝑼 𝑩 = −𝒒 𝟎
𝑨
𝑩
𝑬 ∙ 𝒅𝒔
- because the force is conservative, the line integral does
not depend on the path taken by the charge.
8/15/2014 3

4. • It is the potential energy per unit charge.
• The potential energy is characteristic of the field only.
• The potential energy is characteristic of the charge-field
system.
• The potential is independent of the value of 𝑞0.
• The potential has a value at every point in an electric field.
• Thus, electric potential is given by the equation,
∆𝑽 =
∆𝑼
𝒒
= − 𝑨
𝑩
𝑬 ∙ 𝒅𝒔
• The potential difference between two points exists solely
because of a source charge and depends on the source
charge distribution.
• For a potential energy to exist, there must be a system of two
or more charges.
• The potential energy belongs to the system and changes only
if a charge is moved relatively to the rest of the system.
8/15/2014 4

5. • Assume a charge moves in an electric field without any
change in its kinetic energy. The work performed on the
charge is
𝑾 = ∆𝑼 = 𝒒∆𝑽
• The SI unit of electric potential is 𝑽 =
𝑱
𝑪
• It takes one Joule of work to move a 1 Coulomb charge
through a potential difference of 1V. In addition, 1 N/C = 1
V/m, indicates that the electric field as a measure of the
rate of change of the electric potential with respect to
position.8/15/2014 5

6. • Electric circuits: point of zero potential is defined by
grounding some point in the circuit
• Electric potential due to a point charge at a point in
space: point of zero potential is taken at an infinite
distance from the charge
• With this choice, a potential can be found as
𝑉 = 𝑘 𝑒
𝑞
𝑟
• Note: the potential depends only on charge of an object,
q, and a distance from this object to a point in space, r.
8/15/2014 6

7. • Consider a small charge element 𝑑. Treat is as a point
charge. The potential at some point due to this charge is
𝑑𝑉 = 𝑘
𝑑𝑞
𝑟
• To obtain the total potential at point P, we integrate the
equation above to include contributions from all elements
of the charge distribution. Integrating both sides we get,
𝑉 = 𝑘
𝑑𝑞
𝑟
• The electric potential is taken to be zero when point P is
infinitely far from the charge distribution.
8/15/2014 7

8. • If more than one point charge is present, their electric
potential can be found by applying superposition
principle.
The total electric potential at some point P due to several
point charges is the algebraic sum of the electric
potentials due to the individual charges.
• Remember that potentials are scalar quantities!
8/15/2014 8

9. • Consider a system of two particles
• If V1 is the electric potential due to charge q1 at a point P,
then work required to bring the charge q2 from infinity to P
without acceleration is q2V1. If a distance between P and
q1 is r, then by definition
• 𝑃𝐸 = 𝑞2 𝑉1 = 𝑘 𝑒
𝑞1 𝑞2
𝑟
• Potential energy is positive if charges are of the same sign
and vice versa.
8/15/2014 9
P A
q1
q2
r

10. 8/15/2014 10
Three ions, Na+, Na+, and Cl-, located such, that they
form corners of an equilateral triangle of side 2 nm in
water. What is the electric potential energy of one of the
Na+ ions?
Cl-
Na+ Na+
?
 Na Cl Na Na Na
e e e Cl Na
q q q q q
PE k k k q q
r r r
   
but : !Cl Naq q 
  0Na
e Na Na
q
PE k q q
r
   

11. • Recall that work is opposite of the change in potential
energy,
• No work is required to move a charge between two points
that are at the same potential. That is, W=0 if VB=VA
• Recall:
1. all charge of the charged conductor is located on its surface
2. electric field, E, is always perpendicular to its surface, i.e. no
work is done if charges are moved along the surface
• Thus: potential is constant everywhere on the surface of a
charged conductor in equilibrium
8/15/2014 11
 B AW PE q V V    
… but that’s not all!

12. • Because the electric field is zero inside the conductor, no
work is required to move charges between any two
points, i.e.
• If work is zero, any two points inside the conductor have
the same potential, i.e. potential is constant everywhere
inside a conductor
• Finally, since one of the points can be arbitrarily close to
the surface of the conductor, the electric potential is
constant everywhere inside a conductor and equal to its
value at the surface!
• Note that the potential inside a conductor is not necessarily
zero, even though the interior electric field is always zero!
8/15/2014 12
  0B AW q V V   

13. • A unit of energy commonly used in atomic, nuclear and
particle physics is electron volt (eV)
The electron volt is defined as the energy that electron (or
proton) gains when accelerating through a potential
difference of 1 V
• Relation to SI:
1 eV = 1.60´10-19 C·V = 1.60´10-19 J
8/15/2014 13
Vab=1 V

14. • Remember that potential is a scalar quantity
• Superposition principle is an algebraic sum of potentials due to
a system of charges
• Signs are important
• Just in mechanics, only changes in electric potential are
significant, hence, the point you choose for zero electric
potential is arbitrary.
8/15/2014 14

15. 8/15/2014 15
In the Bohr model of a hydrogen atom, the electron, if it is in the
ground state, orbits the proton at a distance of r = 5.29´10-11 m. Find
the ionization energy of the atom, i.e. the energy required to remove
the electron from the atom.
Note that the Bohr model, the idea of electrons as tiny balls orbiting the nucleus, is not a
very good model of the atom. A better picture is one in which the electron is spread out
around the nucleus in a cloud of varying density; however, the Bohr model does give the
right answer for the ionization energy

16. 8/15/2014 16
In the Bohr model of a hydrogen atom, the electron, if it is in the ground state,
orbits the proton at a distance of r = 5.29 x 10-11 m. Find the ionization energy,
i.e. the energy required to remove the electron from the atom.
Given:
r = 5.292 x 10-11 m
me = 9.1110-31 kg
mp = 1.6710-27 kg
|e| = 1.6010-19 C
Find:
E=?
The ionization energy equals to the total energy of the
electron-proton system,
E PE KE 
22 2
18
2.18 10 J -13.6 eV
2 2
e e
e e
e
m k ee e
E k k
r m r r
 
         
 
The velocity of e can be found by analyzing the force
on the electron. This force is the Coulomb force;
because the electron travels in a circular orbit, the
acceleration will be the centripetal acceleration:
e c cm a F
2 2
,
2
e e
e v
PE k KE m
r
  with
or
2 2
2
,e e
v e
m k
r r
 or
2
2
,e
e
e
v k
m r

Thus, total energy is

17. • They are defined as a surface in space on which the potential
is the same for every point (surfaces of constant voltage)
• The electric field at every point of an equipotential surface is
perpendicular to the surface
8/15/2014 17
convenient to represent by drawing
equipotential lines

18. 8/15/2014 18

19. 1. An automobile headlight is connected to 12 V battery.
The amount of energy transformed is proportional to
how much charge flows, which in turn depends on how
long the light is on. Over a given period, 5 C of charge
flows through the light. How much is the total energy
transformed?
𝑉 =
𝑃𝐸
𝑞
→ 𝑃𝐸 = 𝑉𝑞
𝑃𝐸 = 12 𝑉 5𝐶 = 60𝑉𝐶 = 60 𝐽
8/15/2014 19

20. 2. Two parallel plates are charged to a voltage of 50 V. If
the separation distance between the plates is 0.050 m,
calculate the electric field between them.
𝑉 = 𝐸𝑑 → 𝐸 =
𝑉
𝑑
𝐸 =
50 𝑉
0.050 𝑚
= 1000
𝑉
𝑚
8/15/2014 20

21. 3. Two parallel plates are separated by 0.5 m. An electric
field of 6000 N/C exists between the plates. What is the
potential difference between the plates?
𝑉 = 𝐸𝑑
𝑉 = 6000
𝑁
𝐶
0.5𝑚 = 3000
𝑁𝑚
𝐶
= 3000
𝐽
𝐶
𝑉 = 3000 𝑉
8/15/2014 21

22. 4. System below is composed of three charges. Find the
symbolic expression for the total electric potential energy of
the system.
8/15/2014 22
𝑞1 = 10𝑞
𝑞1 = −5𝑞
𝑞1 = 8𝑞
4𝑑3𝑑

23. 8/15/2014 23
𝒒 𝟏 & 𝒒 𝟐 𝒒 𝟏 & 𝒒 𝟑 𝒒 𝟐 & 𝒒 𝟐
𝑉 = 𝑘
𝑞1 𝑞2
𝑟
𝑉 = 𝑘
𝑞1 𝑞3
𝑟
𝑉 = 𝑘
𝑞2 𝑞3
𝑟
𝑉 = 𝑘
10𝑞 −5𝑞
3𝑑
𝑉 = 𝑘
10𝑞 8𝑞
4𝑑
𝑉 = 𝑘
−5𝑞 8𝑞
5𝑑
𝑉 = −𝑘
50𝑞2
3𝑑
𝑉 = 𝑘
20𝑞2
𝑑
𝑉 = −𝑘
8𝑞2
𝑑
𝑉𝑇 = −𝑘
50𝑞2
3𝑑
+ 𝑘
20𝑞2
𝑑
− 𝑘
8𝑞2
𝑑
𝑉𝑇 =
−14𝑞2 𝑘
3𝑑

24. 1. A particle (charge = 50 𝜇𝐶) moves in a region where the only
force on it is an electric force. As the particle moves 25 cm
from point A to B, its kinetic energy increases by 1.5 mJ.
Determine the electric potential difference 𝑉𝐵 − 𝑉𝐴.
2. Points A at ( 2, 3)m and B at ( 5, 7)m are in region where the
electric field is uniform and given by 𝐸 = 4 𝑖 + 3 𝑗 𝑁/𝐶. What is the
potential difference 𝑉𝐴 − 𝑉𝐵?
3. Calculate the total electric potential at point A and B given
𝑄1 = 2.00 × 10−6 𝐶, 𝑄2 = 1.00 × 10−6 𝐶, 𝑄3 = −4.00 × 10−6 𝐶,
8/15/2014 24
𝑄1 𝐴𝑄3𝑄2 𝐵
.200𝑚 .200𝑚 .300𝑚 .200𝑚

25. • Physics 2 – Calculus Based Physics by Stewart
• Lecture Guide Calculus Based Physics
8/15/2014 25

26. GROUP 1 GROUP 2 GROUP 3
CLASS # 1-5 CLASS # 6-10 CLASS # 11-15
GROUP 4 GROUP 5 GROUP 6
CLASS 16-20 CLASS 21-25 CLASS # 26-31
8/15/2014 26
1. COPY THIS LECTURE.
2. STUDY!!!
3. PER GROUP: PLEASE BRING MANILA PAPER, PENTEL PEN
NEXT MEETING AND READY FOR “READY FOR THIS” 

27. GROUP 1 Group 2
Ausan, Tantiongco, Mendros,
Limtuico, Anacito
Dingalan, Decierdo, Baguhin,
Villanueva, Cruz
Group 3 Group 4
Estrella, Esguerra, Estrada, Dupaya,
Nonsol
Campos, Quintil, Nunez, Zabala,
Teves
Group 5 Group 6
Bibat, Alcaide, Albaniel, Gargar,
Gonzales
Dela Cruz, Peredo, Ogania, Toledo,
Soriano
8/15/2014 27
1. COPY THIS LECTURE.
2. STUDY!!!
3. PER GROUP: PLEASE BRING MANILA PAPER, PENTEL PEN NEXT
MEETING AND READY FOR “READY FOR THIS” 

28. GROUP 1 GROUP 2
Acotanza, Calingasan, Canezal,
Perolina, Rivera
Morga, Opog, Pontemayor, Roadiel,
Tolentino
GROUP 3 GROUP 4
Balde, Castillo, Castro, Cruz,
Dumaguit
Amlon, Anduque, Fadri, Micua, Morillo
GROUP 5 GROUP 6
Mendez, Pagdanganan, Panol,
Peralta, Santos
Gatchalian, Narvacan, Ratin, Sibuan,
Simon
8/15/2014 28
1. COPY THIS LECTURE.
2. STUDY!!!
3. PER GROUP: PLEASE BRING MANILA PAPER, PENTEL PEN NEXT
MEETING AND READY FOR “READY FOR THIS” 