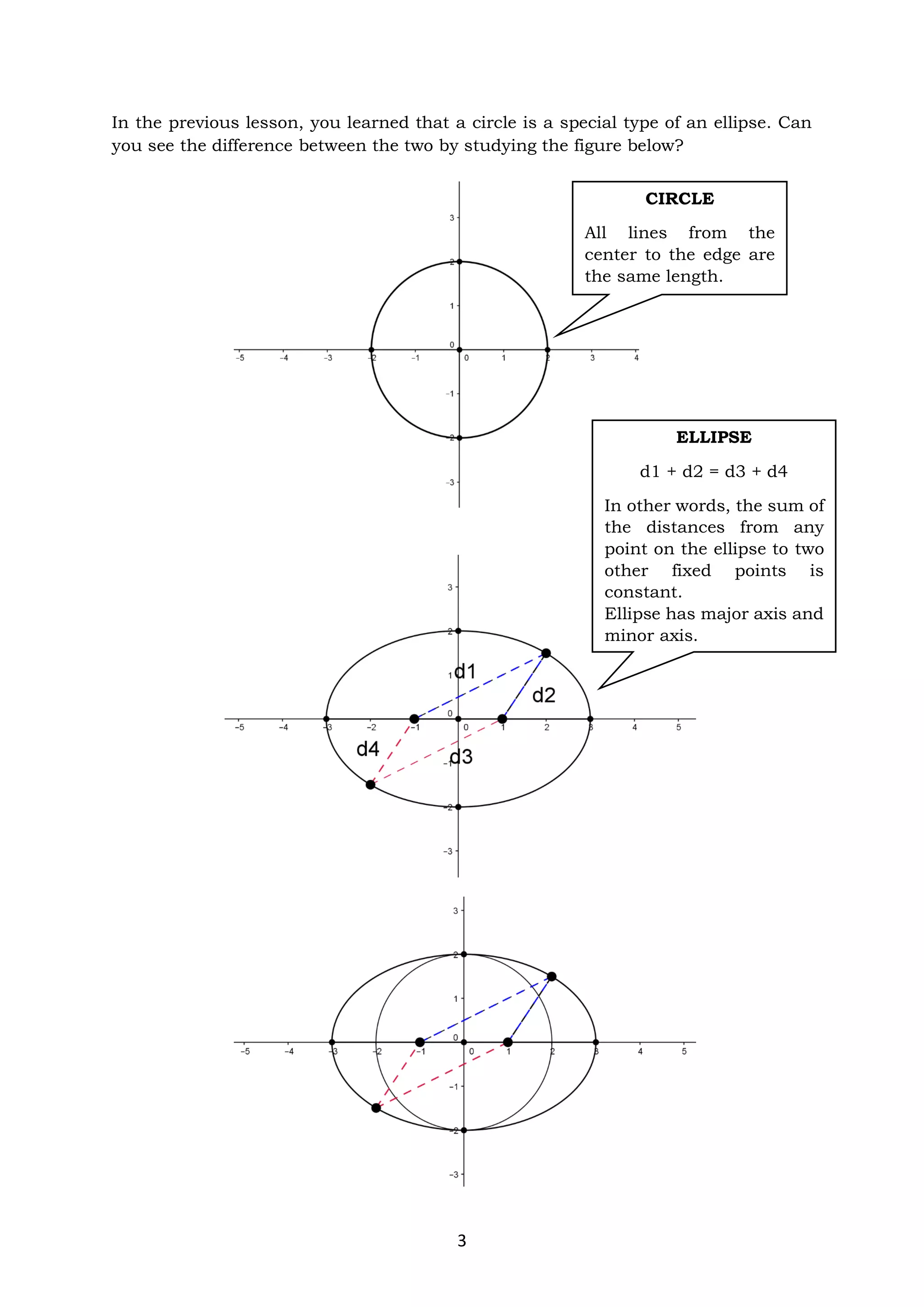
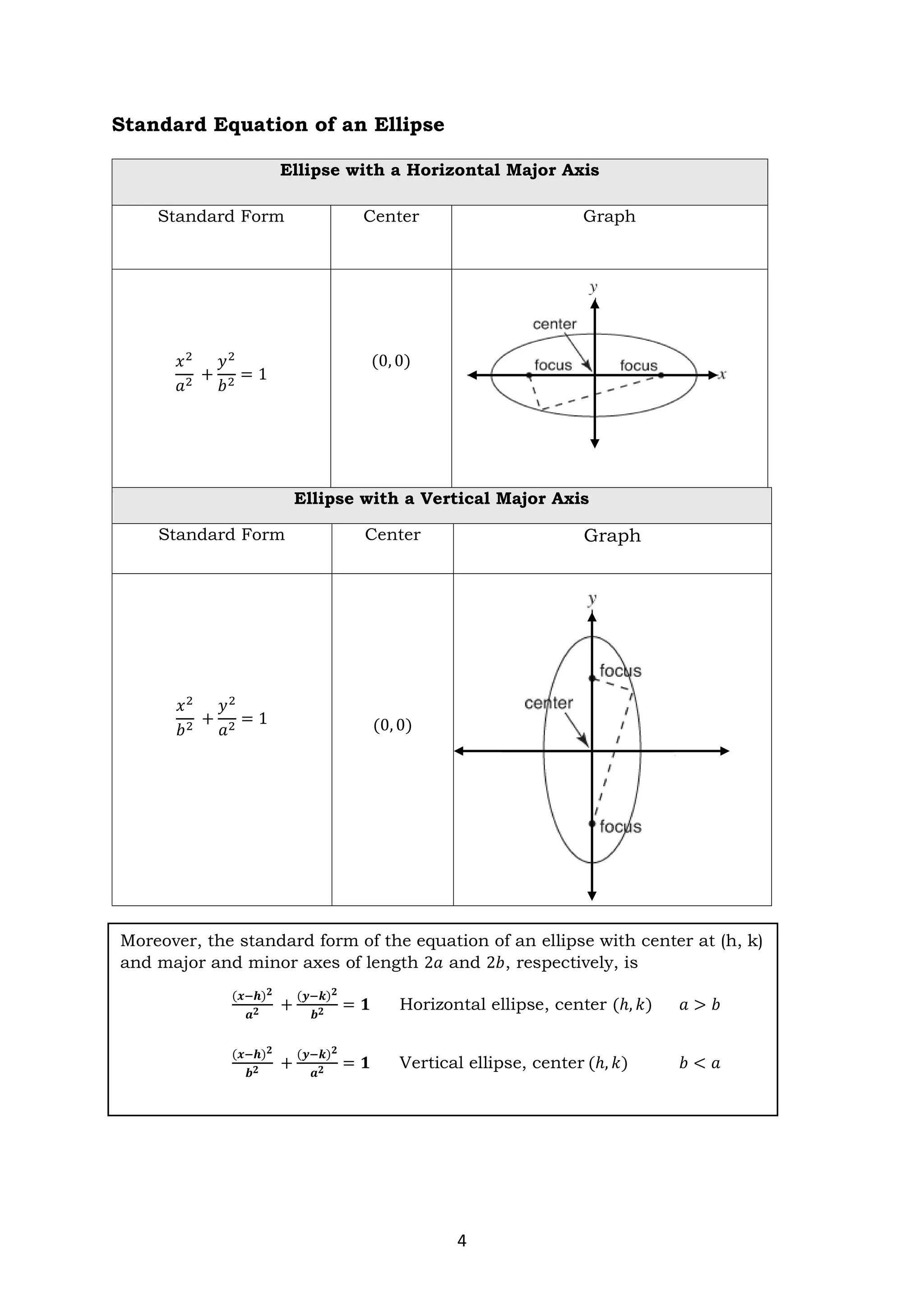
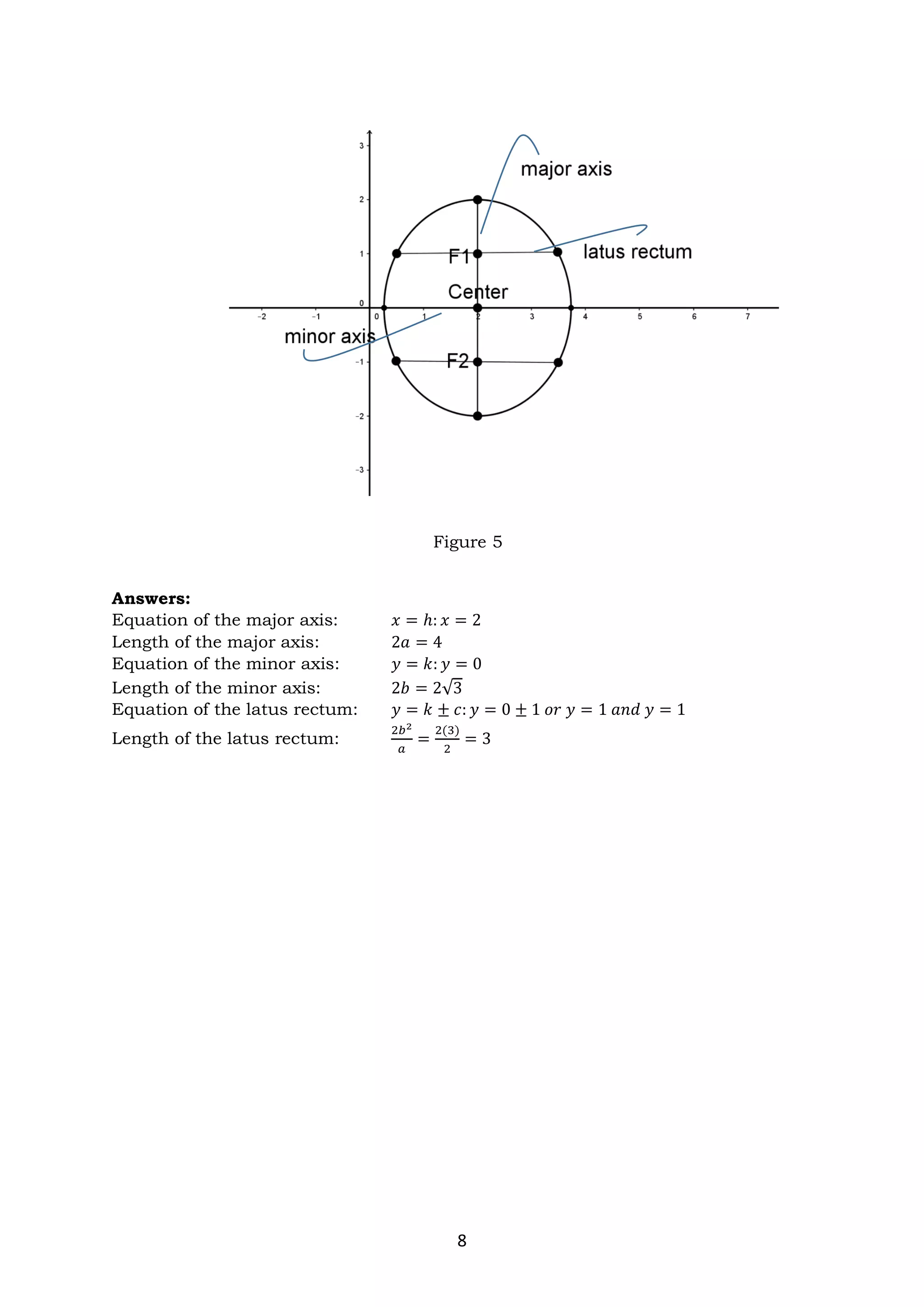
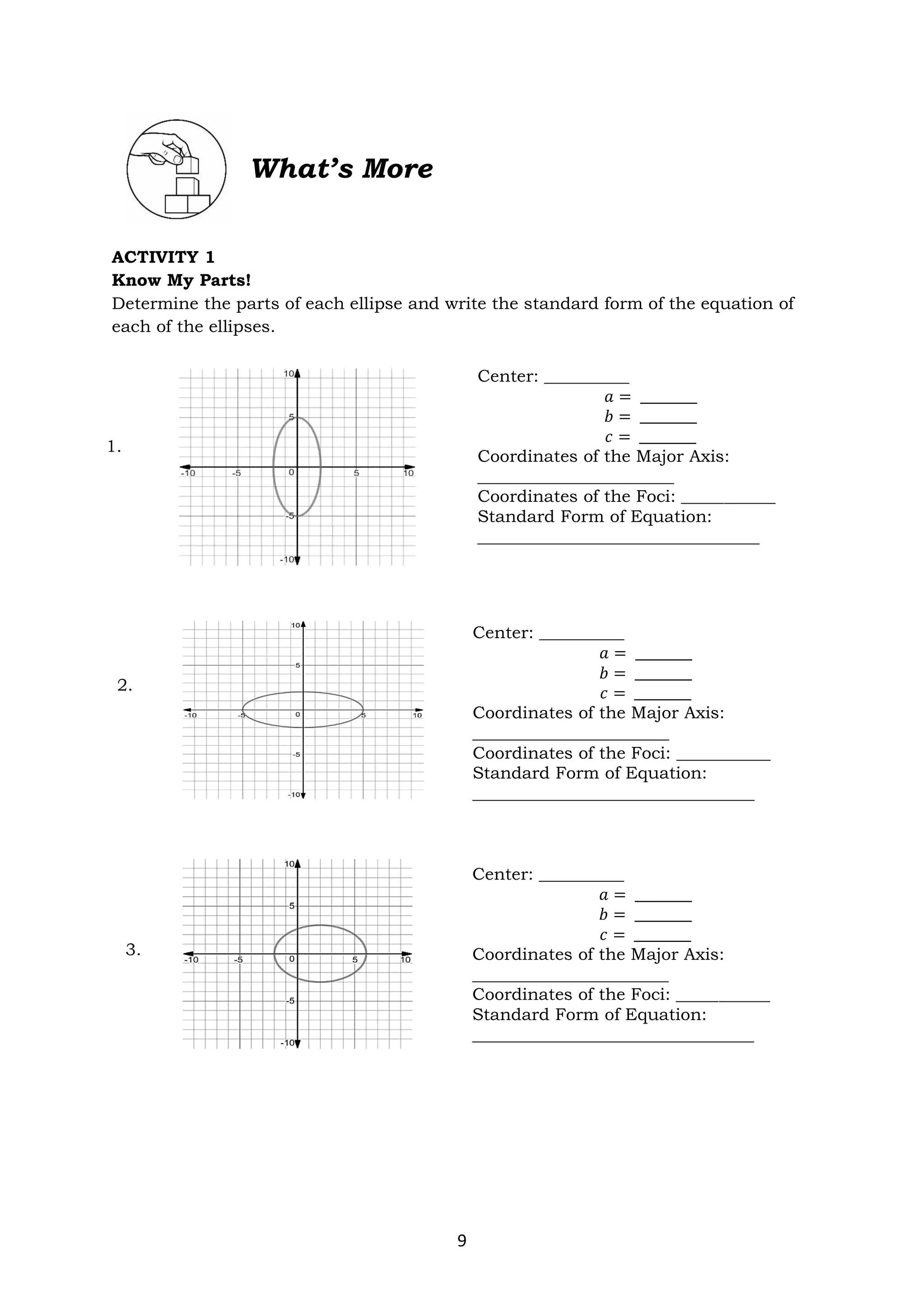
The document discusses ellipses and their key properties. It defines an ellipse as the set of points where the sum of the distances to two fixed foci is constant. Examples are given showing how to identify the center, vertices, covertices, and foci of ellipses given their equations. It also explains how to write the standard form of the equation of an ellipse and determines whether it has a horizontal or vertical major axis. Activities are provided for students to practice identifying parts of ellipses and writing their standard forms from equations.

1. Pre-Calculus
Quarter 1 – Module 3:
Ellipses

2. 1
What’s New
Did you experience hiking to Mt. Samat, Bataan? You'll view the Colonnade
from the footpath that ends up in the Memorial Cross and the elliptical designs as
shown in the photo represent an ellipse. This module will bring you to the extremely
important type of conic section, an ellipse, and probably make comprehensive use in
real- world. A football ball, satellite, planet orbit, tunnel and dome are just few
examples of elliptical shapes. Ellipses have also properties to be considered within
the application of the real world. These applications are going to be discussed within
the succeeding lesson.
Mt. Samat, Pilar, Bataan, by ChaseJase, 10 June 2020,
https://chasejaseph.com/mt-samat-national-shrine-travel-guide/

3. 2
Lesson
3 Ellipses
.
What’s In
Definition of an Ellipse
An ellipse is the set of all points (𝑥, 𝑦) in a plane such that the sum of the distances
from any point on the ellipse to two other fixed points is constant. The two fixed
points are called the foci (plural of focus) of the ellipse. Figure 1 shows a picture of
an ellipse.
Parts of an Ellipse
Foci: The two fixed points on the major axis of an ellipse such that the sum of the
distances from these points to any point (𝑥, 𝑦) on the ellipse is constant
Center: The point halfway between the foci
Major axis: The line segment containing the foci of an ellipse with both endpoints on
the ellipse
Minor axis: The line segment perpendicular to the major axis and passing through
the center, with both endpoints on the ellipse
Vertices: The endpoints of the major axis
Covertices: The endpoints of the minor axis
Latus Rectum: The chord of the ellipse through its one focus and perpendicular to
the major axis
Figure 1

4. 3
In the previous lesson, you learned that a circle is a special type of an ellipse. Can
you see the difference between the two by studying the figure below?
CIRCLE
All lines from the
center to the edge are
the same length.
Equation: x2 + y2 = 22
ELLIPSE
d1 + d2 = d3 + d4
In other words, the sum of
the distances from any
point on the ellipse to two
other fixed points is
constant.
Ellipse has major axis and
minor axis.

5. 4
Standard Equation of an Ellipse
Ellipse with a Horizontal Major Axis
Standard Form Center Graph
𝑥2
𝑎2
+
𝑦2
𝑏2
= 1
(0, 0)
Ellipse with a Vertical Major Axis
Standard Form Center Graph
𝑥2
𝑏2
+
𝑦2
𝑎2
= 1 (0, 0)
Moreover, the standard form of the equation of an ellipse with center at (h, k)
and major and minor axes of length 2𝑎 and 2𝑏, respectively, is
(𝒙−𝒉)𝟐
𝒂𝟐 +
(𝒚−𝒌)𝟐
𝒃𝟐 = 𝟏 Horizontal ellipse, center (ℎ, 𝑘) 𝑎 > 𝑏
(𝒙−𝒉)𝟐
𝒃𝟐 +
(𝒚−𝒌)𝟐
𝒂𝟐 = 𝟏 Vertical ellipse, center (ℎ, 𝑘) 𝑏 < 𝑎

6. 5
Example 1. Sketch and identify the center, vertices, and covertices of the ellipse
with equation,
𝑥2
25
+
𝑦2
49
= 1.
Solution
Because the denominator of the y2-term is greater than the denominator of the
x2-term, you can conclude that the major axis is vertical whose center is at the
origin. Moreover, because 𝑎2
49, 𝑡ℎ𝑒𝑛 𝑎 = 7, the vertices are (0, 7) and (0, -7). Finally,
because 𝑏2
= 25, 𝑡ℎ𝑒𝑛 𝑏 = 5, the covertices are (-5, 0) and (5, 0). The graph is shown
in Figure 2.
Example 2. Find the standard form of the equation of the ellipse having foci at
(-1, 2) and (3,2) a major axis of length 8, as shown in Figure 3.
Figure 2
Figure 3

7. 6
Solution
The foci occur at (-1,2) and (3,2). The midway between (-1, 2) and (3, 2) is the point
(1, 2). This is the center of the ellipse. Now, the distance from the center to one of
the foci is 2 units or 𝑐 = 2.
Since the foci and the center of an ellipse are on the major axis, you can visualize
that the ellipse is horizontal. The length of the major axis is 2𝑎 = 8. Thus, 𝑎 = 4.
Then, from 𝑐2
= 𝑎2
− 𝑏2
, you can derive a formula to find 𝑏2
. So, 𝑏2
= 𝑎2
− 𝑐2
. And by
plugging in, 𝑏2
= 42
− 22
= 12.
Using the template for the ellipse with horizontal axis at (h, k)
(𝑥−ℎ)2
𝑎2 +
(𝑦−𝑘)2
𝑏2 = 1,
the standard equation of the above ellipse with Center: (1,2) ; 𝑎2
= 16; 𝑏2
= 12 is
(𝑥−1)2
16
+
(𝑦−2)2
12
= 1.
Example 3. Write the equation of the ellipse in standard form, then find the center,
vertices, and foci of the ellipse with the equation, 𝑥2
+ 4𝑦2
+ 6𝑥 − 8𝑦 + 9 = 0.
Solution
By completing the square, you can write the original equation in standard form.
𝑥2
+ 4𝑦2
+ 6𝑥 − 8𝑦 + 9 = 0 Write the original equation.
(𝑥2
+ 6𝑥 + _____) + 4(𝑦2
− 2𝑦 + _____) = −9 Group terms and factor 4 out of y-terms.
(𝑥2
+ 6𝑥 + 𝟗) + 4(𝑦2
− 2𝑦 + 𝟏) = −9 + 𝟗 + 𝟒(𝟏)
(𝑥 + 3)2
+ 4(𝑦 − 1)2
= 4 Write in completed square form.
(𝑥+3)2
4
+
4(𝑦−1)2
4
=
4
4
Divide all terms by 4.
(𝑥+3)2
22 +
(𝑦−1)2
12 = 1 Write in standard form.
The major axis defined by the given equation is horizontal, where ℎ = −3, 𝑘 = 1,
𝑎 = 2, 𝑏 = 1, and 𝑐 = √𝑎2 − 𝑏2 = √22 − 12 = √3.
Looking at Figure 4, you have the following.
Center: (-3, 1)
Vertices: (-5, 1) and (-1, 1)
Covertices: (-3, 0) and (-3, 2)
Foci: (-3 - √3, 1) and (-3 + √3, 1)

8. 7
Example 4. Express the equation of the ellipse in standard form defined by
4𝑥2
+ 3𝑦2
− 16𝑥 + 4 = 0. Determine the equation and the length of the major axis,
the minor axis, and the length of the latus rectum. Draw the ellipse.
Solution
Transform the equation in standard form by completing the square.
4𝑥2
+ 3𝑦2
− 16𝑥 + 4 = 0 Write the original equation.
4(𝑥2
− 4𝑥 + _____) + 3𝑦2
= −4 Group terms and factor 4 out of x-terms.
4(𝑥2
− 4𝑥 + 𝟒) + 3𝑦2
= −4 + 𝟏𝟔
4(𝑥 − 2)2
+ 3𝑦2
= 12 Write in completed square form.
4(𝑥−2)2
12
+
3𝑦2
12
=
12
12
Divide all terms by12.
(𝑥−2)2
3
+
3𝑦2
4
= 1 Write in standard form.
The center (ℎ, 𝑘) is at (2, 0). Since the denominator of the y2-term is larger than the
denominator of the x2-term, the ellipse has a vertical axis and with
𝑎2
= 4, 𝑎 = 2 and 𝑏2
= 3, 𝑏 = √3, using the formula, 𝑐2
= 𝑎2
− 𝑏2
, 𝑐 = 1. A sketch is a
great help in understanding the graph of an ellipse. See Figure 5.
Figure 4

9. 8
Answers:
Equation of the major axis: 𝑥 = ℎ: 𝑥 = 2
Length of the major axis: 2𝑎 = 4
Equation of the minor axis: 𝑦 = 𝑘: 𝑦 = 0
Length of the minor axis: 2𝑏 = 2√3
Equation of the latus rectum: 𝑦 = 𝑘 ± 𝑐: 𝑦 = 0 ± 1 𝑜𝑟 𝑦 = 1 𝑎𝑛𝑑 𝑦 = 1
Length of the latus rectum:
2𝑏2
𝑎
=
2(3)
2
= 3
Figure 5

10. 9
What’s More
ACTIVITY 1
Know My Parts!
Determine the parts of each ellipse and write the standard form of the equation of
each of the ellipses.
Center: __________
𝑎 = _________
𝑏 = _________
𝑐 = _________
Coordinates of the Major Axis:
_______________________
Coordinates of the Foci: ___________
Standard Form of Equation:
_________________________________
1.
2.
3.
Center: __________
𝑎 = _________
𝑏 = _________
𝑐 = _________
Coordinates of the Major Axis:
_______________________
Coordinates of the Foci: ___________
Standard Form of Equation:
_________________________________
Center: __________
𝑎 = _________
𝑏 = _________
𝑐 = _________
Coordinates of the Major Axis:
_______________________
Coordinates of the Foci: ___________
Standard Form of Equation:
_________________________________

11. 10
1.
𝑥2
36
+
𝑦2
16
= 1
2.
𝑥2
9
+
𝑦2
81
= 1 3.
(𝑦−1)2
16
+
(𝑥−1)2
4
= 1
4.
(𝑦+2)2
4
+
(𝑥−2)2
9
= 1
ACTIVITY 1
SKETCH MY GRAPH AND LABEL ALL MY PARTS!
ACTIVITY 2
KNOW MY STANDARD!
Express each equation of the ellipse in standard form. Then determine if the major
axis is horizontal or vertical.
1. 4𝑥2
+ 9𝑦2
= 36
2. 25𝑥2
+ 𝑦2
= 25
3. 16𝑥2
+ 25𝑦2
− 32𝑥 + 50𝑦 + 16 = 0
4. 12𝑥2
+ 20𝑦2
− 12𝑥 + 40𝑦 − 37 = 0
5. 9𝑥2
+ 4𝑦2
+ 36𝑥 − 24𝑦 + 36 = 0
Find the standard equation of the ellipse with the specified condition.
6. The minor axis has a length of 8, foci 5 units below and above the center
(-2,4).
7. The vertices are (-2, 4) and (8, 4) and a focus is at (6, 4).
8. The major axis has a length of 22 and the foci, 9 units to the left and to
the right of the center (2,4).
9. The covertices are (-4,8) and (10,8) and a focus is at (3,12).
10. The center is at (5,3), horizontal major axis of length 20 and minor axis
of length 10.

12. 11
What I Have Learned
In this module, I learned that:
1. An ______________ is the set of all points (x, y) in a plane, the sum of whose
distances from two distinct fixed points is constant.
2. The chord joining the vertices of an ellipse is called ______________, and its
midpoint is the ___________________ of the ellipse.
3. The chord perpendicular to the major axis at the center of an ellipse is called
________________ of the ellipse.
4. The standard form of equation of the horizontal ellipse with center at the origin
is _____________________.
5. Given the center at (h, k) and the ellipse has horizontal axis, the standard
form of equation of the ellipse is _____________________.
6. Given the center at (h, k) and the ellipse has vertical axis, the standard form
of equation of the ellipse is _____________________.
7. The ____________ and _____________ are always colinear with the center of the
ellipse.
8. To find the focus c, when a and b are given, use the formula _____________.

13. For inquiries or feedback, please write or call:
Department of Education – Region III,
Schools Division of Bataan - Curriculum Implementation Division
Learning Resources Management and Development Section (LRMDS)
Phase III, Talisay, Balanga City, Bataan, Philippines, 2100
Telefax: (047) 633-6686
Email Address: balanga.city@deped.gov.ph