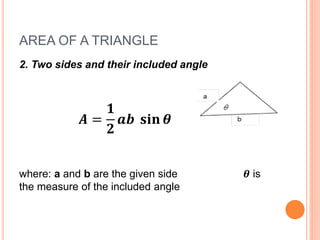
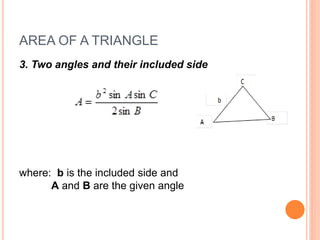
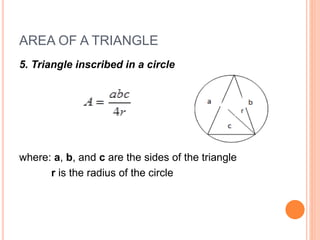
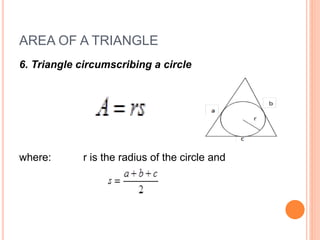
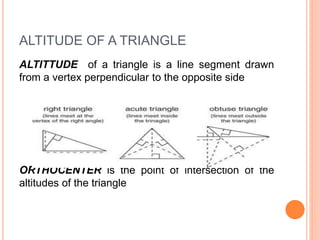
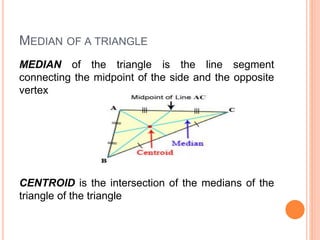
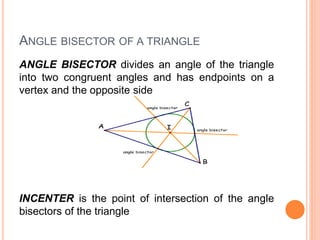
This document defines and explains different types of triangles based on their sides and angles. It discusses equilateral, isosceles, scalene, right, obtuse, and acute triangles. It also covers calculating the perimeter, area, altitude, median, angle bisector, and inscribed/circumscribed triangles. Formulas are provided for calculating the altitude, median, angle bisector, and area using different known properties of triangles. Sample problems are included at the end to test understanding.

1. TRIANGLES

2. CLASSIFICATION OF TRIANGLES
ACCORDING TO SIDES
EQUILATERAL TRIANGLE
- a triangle with three congruent sides
and three congruent angles.
ISOSCELES TRIANGLE
- a triangle with two congruent sides
and two congruent angles.
SCALENE TRIANGLE
- a triangle with no congruent sides and
no congruent angles

3. CLASSIFICATION OF TRIANGLES ACCORDING
TO ANGLES
RIGHT TRIANGLE
- a right triangles with right angle (90
degrees)
OBLIQUE TRIANGLE
- a triangle with no right angle
a. ACUTE TRIANGLE – a triangle with three
acute angles
b. EQUIANGULAR TRIANGLE – a triangle
with three congruent angles
c. OBTUSE – a triangle with one obtuse
angles and two acute angles

4. PERIMETER OF A TRIANGLE
The Perimeter, P, of a triangle is the sum of
the lengths of its three sides
P = a + b + c
where: a, b and c are the lengths of the sides of the
given triangle


5. AREA OF A TRIANGLE
1. Base and Altitude are given
where: b is the length of the base
h is the altitude
bhA
2
1


6. AREA OF A TRIANGLE
2. Two sides and their included angle
𝑨 =
𝟏
𝟐
𝒂𝒃 𝐬𝐢𝐧 𝜽
where: a and b are the given side 𝜽 is
the measure of the included angle

7. AREA OF A TRIANGLE
3. Two angles and their included side
where: b is the included side and
A and B are the given angle

8. AREA OF A TRIANGLE
4. Three sides are given
Heron’s Formula
where s is the semi-perimeter of the triangle

9. AREA OF A TRIANGLE
5. Triangle inscribed in a circle
where: a, b, and c are the sides of the triangle
r is the radius of the circle

10. AREA OF A TRIANGLE
6. Triangle circumscribing a circle
where: r is the radius of the circle and

11. ALTITUDE OF A TRIANGLE
ALTITTUDE of a triangle is a line segment drawn
from a vertex perpendicular to the opposite side
ORTHOCENTER is the point of intersection of the
altitudes of the triangle

12. ALTITUDE OF A TRIANGLE (FORMULA)
To compute the altitude of a triangle,
𝒉 =
𝟐 𝒔 𝒔 − 𝒂 𝒔 − 𝒃 𝒔 − 𝒄
𝒄
Where h is the altitude of the triangle
a, b and c are the sides of the triangle

13. MEDIAN OF A TRIANGLE
MEDIAN of the triangle is the line segment
connecting the midpoint of the side and the opposite
vertex
CENTROID is the intersection of the medians of the
triangle of the triangle

14. MEDIAN OF THE TRIANGLE (FORMULA)
To compute the median of the triangle,
𝒎 =
𝟏
𝟐
𝟐𝒂 𝟐 + 𝒃 𝟐 − 𝒄 𝟐
Where m is the median of the triangle
a, b and c are the sides of the triangle

15. ANGLE BISECTOR OF A TRIANGLE
ANGLE BISECTOR divides an angle of the triangle
into two congruent angles and has endpoints on a
vertex and the opposite side
INCENTER is the point of intersection of the angle
bisectors of the triangle

16. ANGLE BISECTOR OF A TRIANGLE
(FORMULA)
To compute the angle bisector of a triangle,
𝑰 =
𝒂𝒃 𝒂 + 𝒃 𝟐 − 𝒄 𝟐
𝒂 + 𝒃
Where I is the angle bisector of the triangle
a, b and c are the sides if the triangle

17. QUIZ (ES12KA3)
1. Find the altitude and the area of an equilateral
triangle whose side is 8 cm. long.
(Ans.: 4 3 cm, 16 3 𝑐𝑚2)
2. Find the area of an equilateral triangle if its altitude
is 5 cm. (Ans.: 14.43 𝑐𝑚2)
3. The base of an isosceles triangle and the altitude
drawn from one of the congruent sides are equal to
18 cm. and 15 cm., respectively. Find the lengths of
the sides of the triangle.
(Ans.: 16.28 cm.)

18. 4. In a right triangle, the bisector of the right angle
divides the hypotenuse in the ratio of 3 is to 5.
Determine the measures of the acute angles of the
triangle. (Ans.: 59˚ and 31˚)
5. The lengths of the sides of a triangle are in the ratio
ratio of 17:10:9. Find the lengths of the three sides if
if the area of the triangle is 576 square centimeter.
(Ans.: 68cm, 40cm and 36cm)
6. In an acute triangle ABC, an altitude AD is drawn.
drawn. Find the area of the triangle ABC if 𝐴𝐵 =
15 𝑖𝑛. , 𝐴𝐶 = 18 𝑖𝑛., and 𝐵𝐷 = 10 𝑖𝑛.
(Ans.: 134.8 square inches)

19. Note to ES12KA3:
1. This assessment will be recorded as your Quiz #2.
2. Show your complete solution and box your final
answer with red-ink pen. Erasures are not
allowed.
3. Copy and answer. Use short bond paper only.
4. Deadline is on Wednesday, December 2, 2105.
Submit your assessment “individually” at Math and
Physics Department Faculty until 1:30 pm only.
5. Late of submission will no longer be accepted.