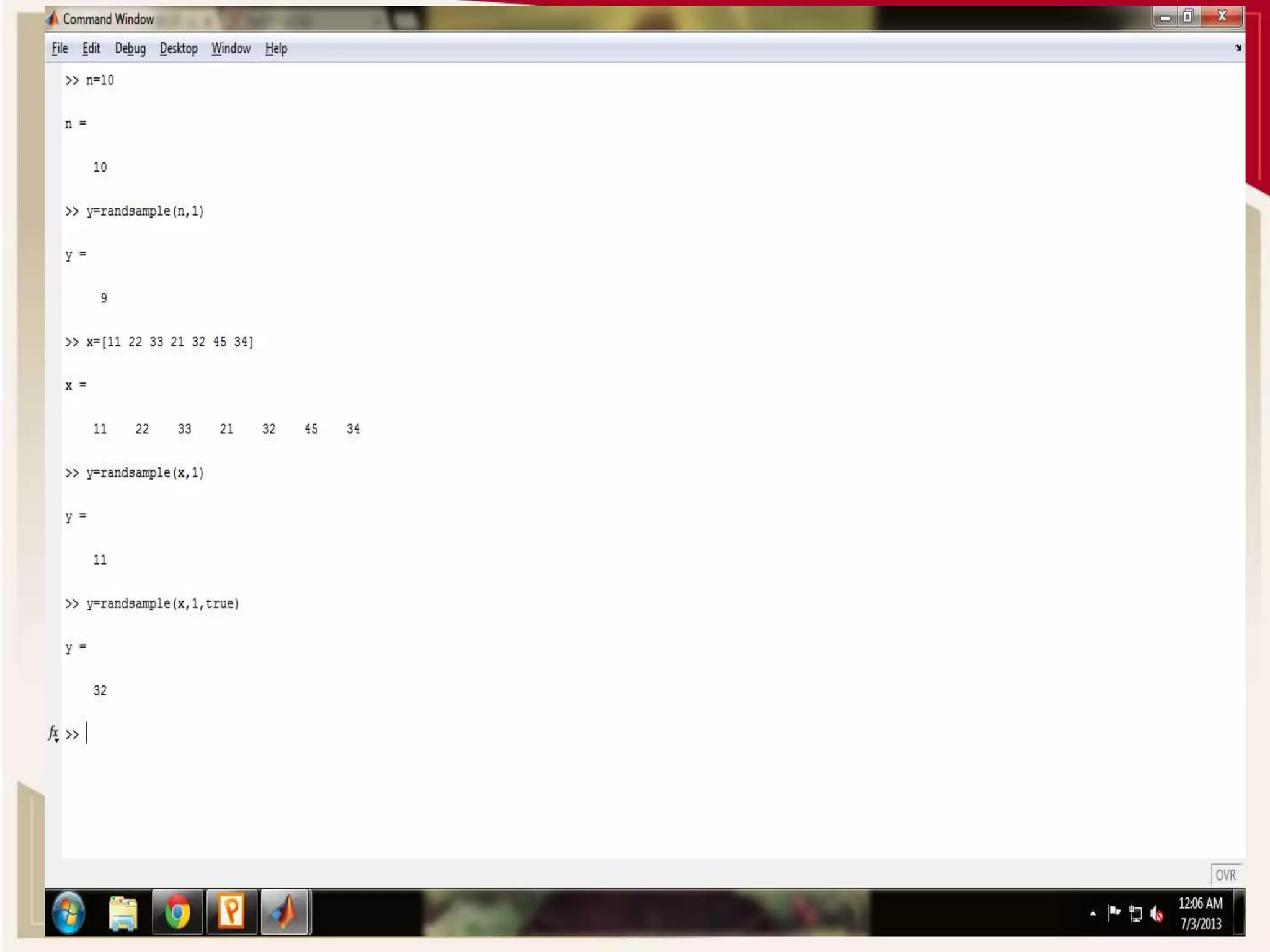
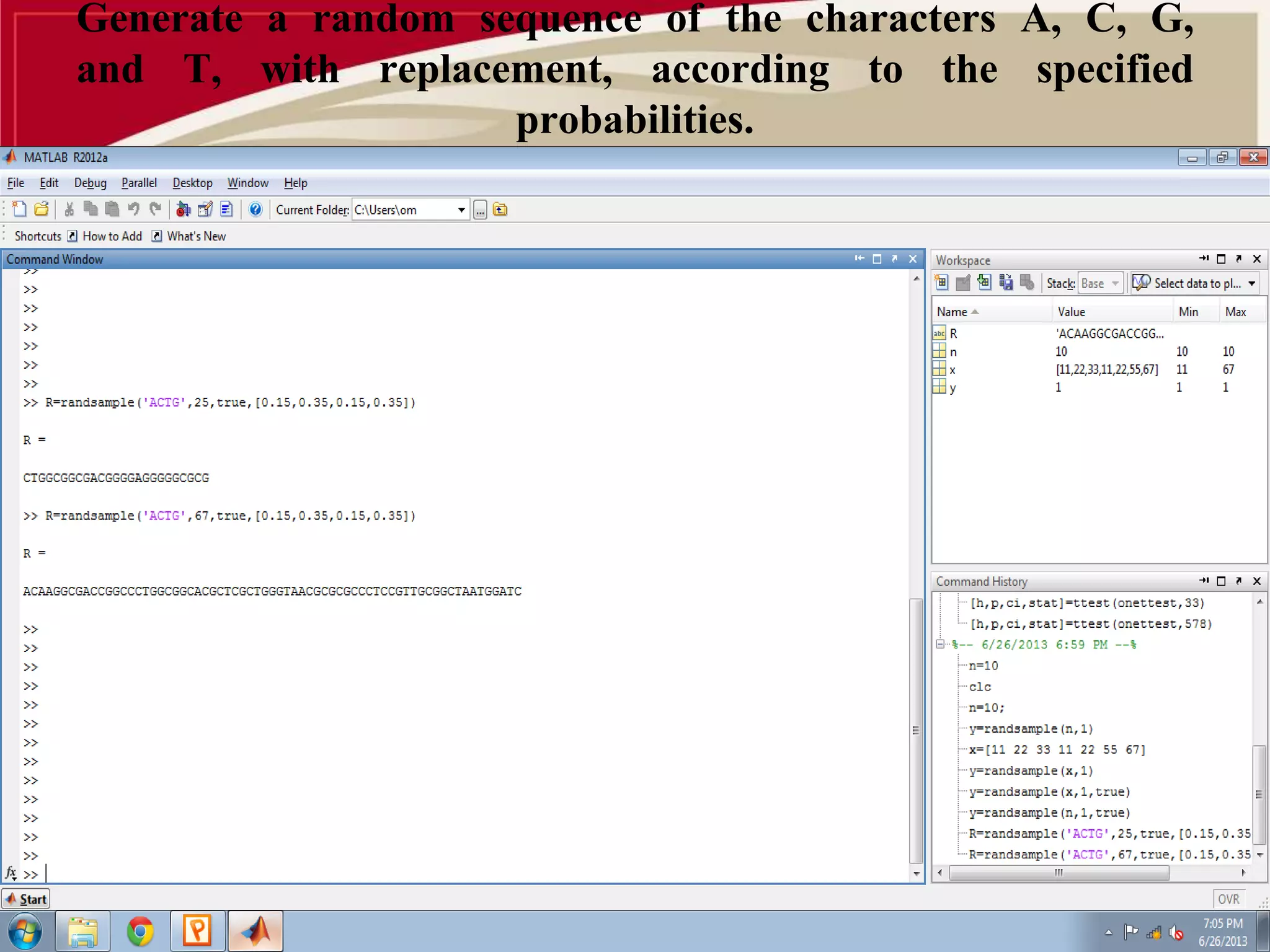
This document provides an overview of sampling and hypothesis testing in MATLAB. It discusses simple random sampling, random sampling functions in MATLAB, and the basics of hypothesis testing. It then describes various parametric tests that can be performed in MATLAB, including one sample t-test, paired t-test, two sample t-test, z-test, and F-test. Examples of how to perform each test in MATLAB are also provided.






![Hypothesis Tests:
A hypothesis test is a procedure for determining
if an assertion about a characteristic of a
population is correct.
In hypothesis testing, the goal is to see if there is
sufficient statistical evidence to accept a
presumed null hypothesis or to reject
the alternative hypothesis[1].
The null hypothesis is usually denoted H0 while
the alternative hypothesis is usually denoted H1.](https://image.slidesharecdn.com/parametrictest-141109021327-conversion-gate01/75/Parametric-test-9-2048.jpg)

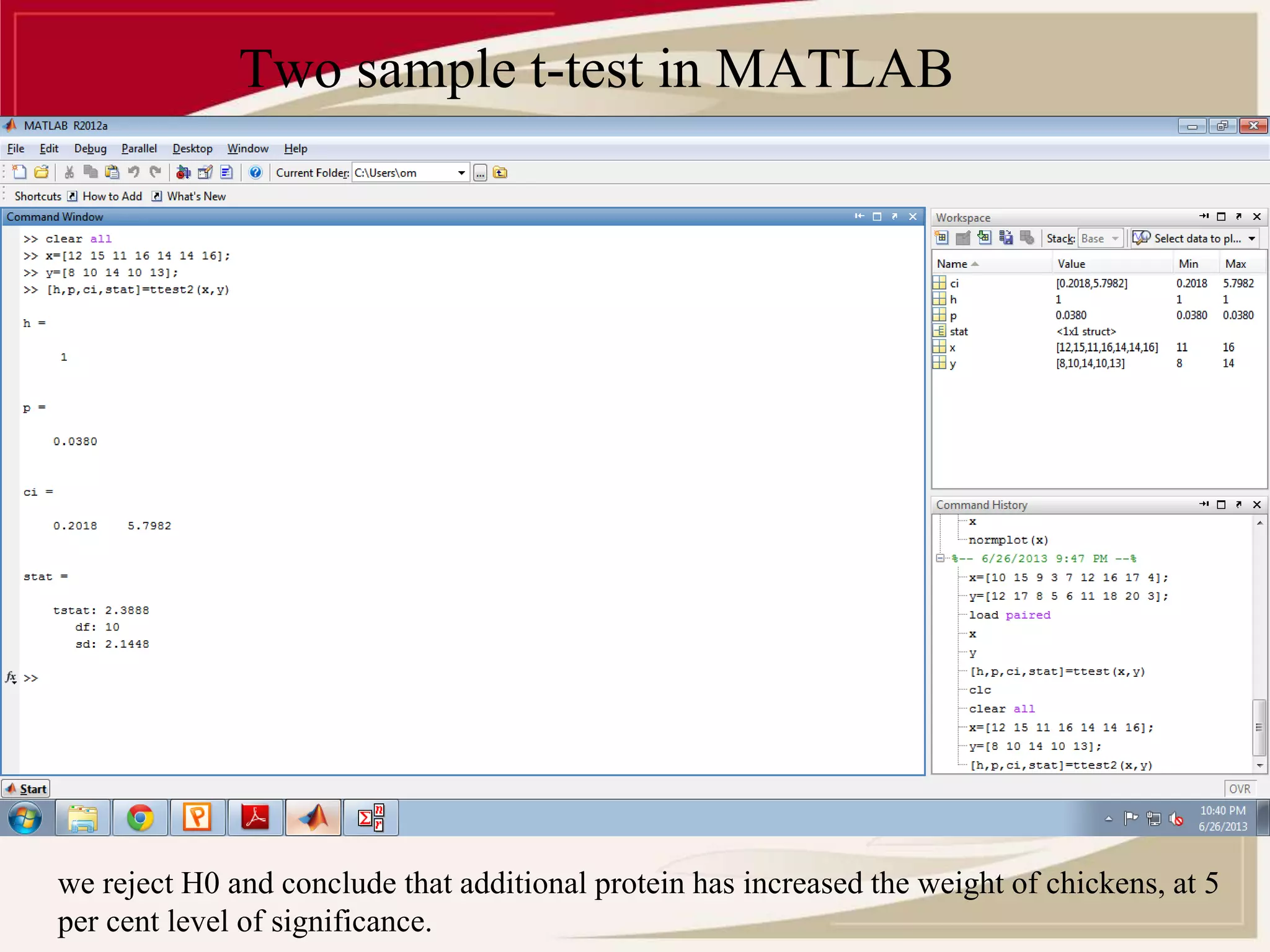
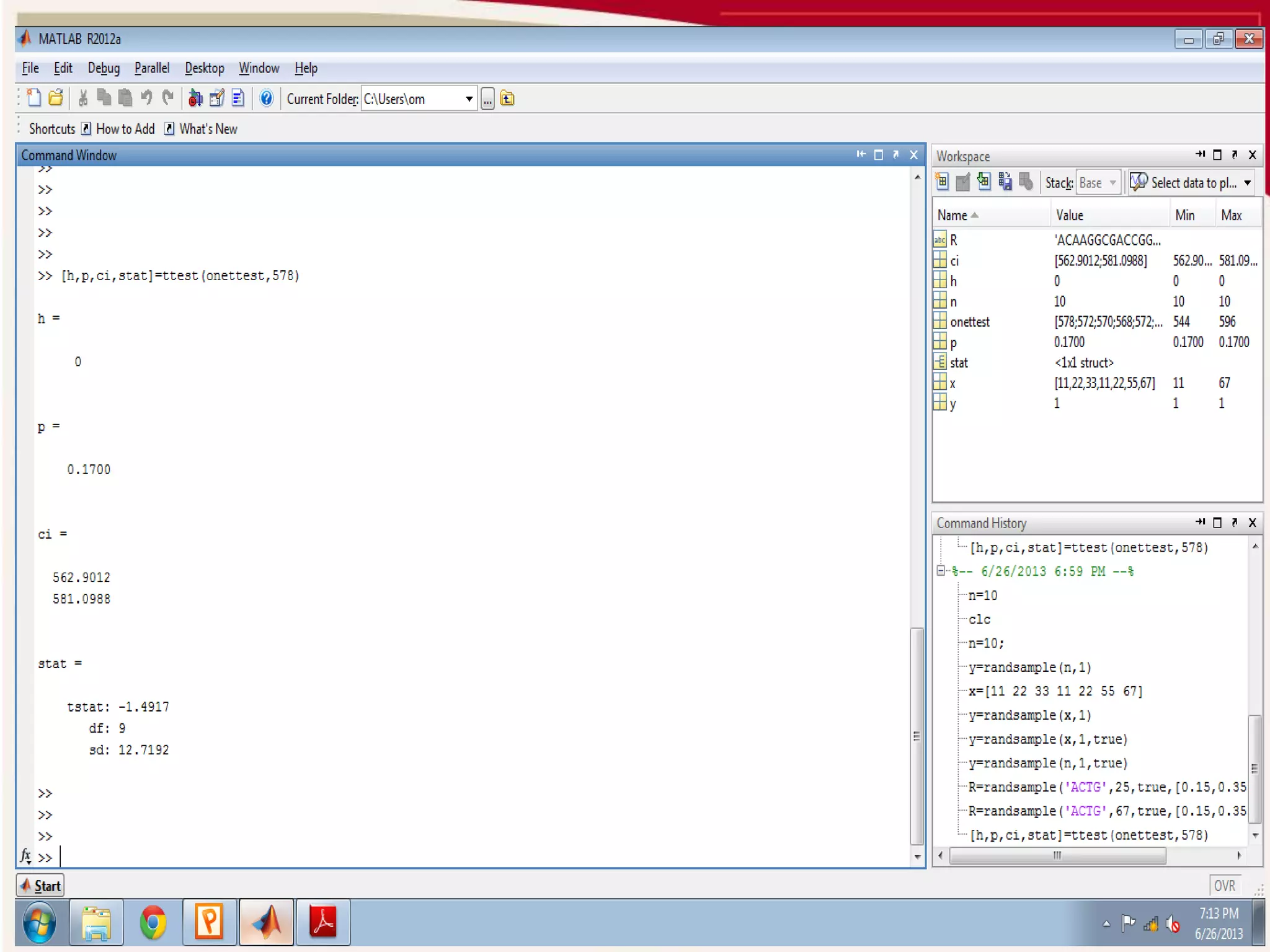
![One sample t-test:
[h,p,ci,stat] = ttest(X,M) performs a t-test of the hypothesis that
the data in X come from a distribution with mean M.
CI returns a 100*(1-ALPHA)% confidence interval for the true
mean of X.
STATS returns a structure with the following fields:
'tstat' -- the value of the test statistic
'df' -- the degrees of freedom of the test
'sd' -- the estimated population standard deviation.](https://image.slidesharecdn.com/parametrictest-141109021327-conversion-gate01/75/Parametric-test-11-2048.jpg)

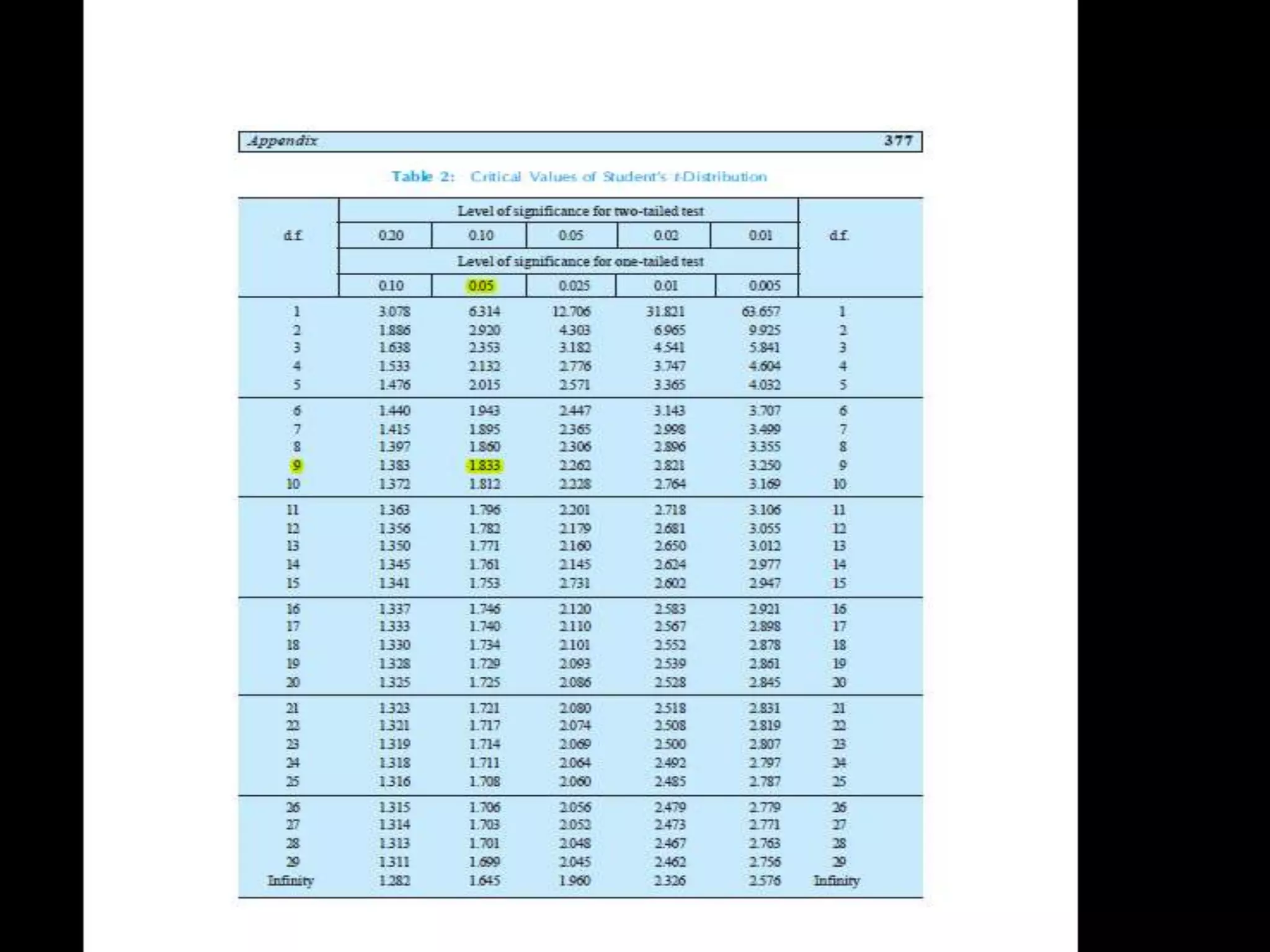
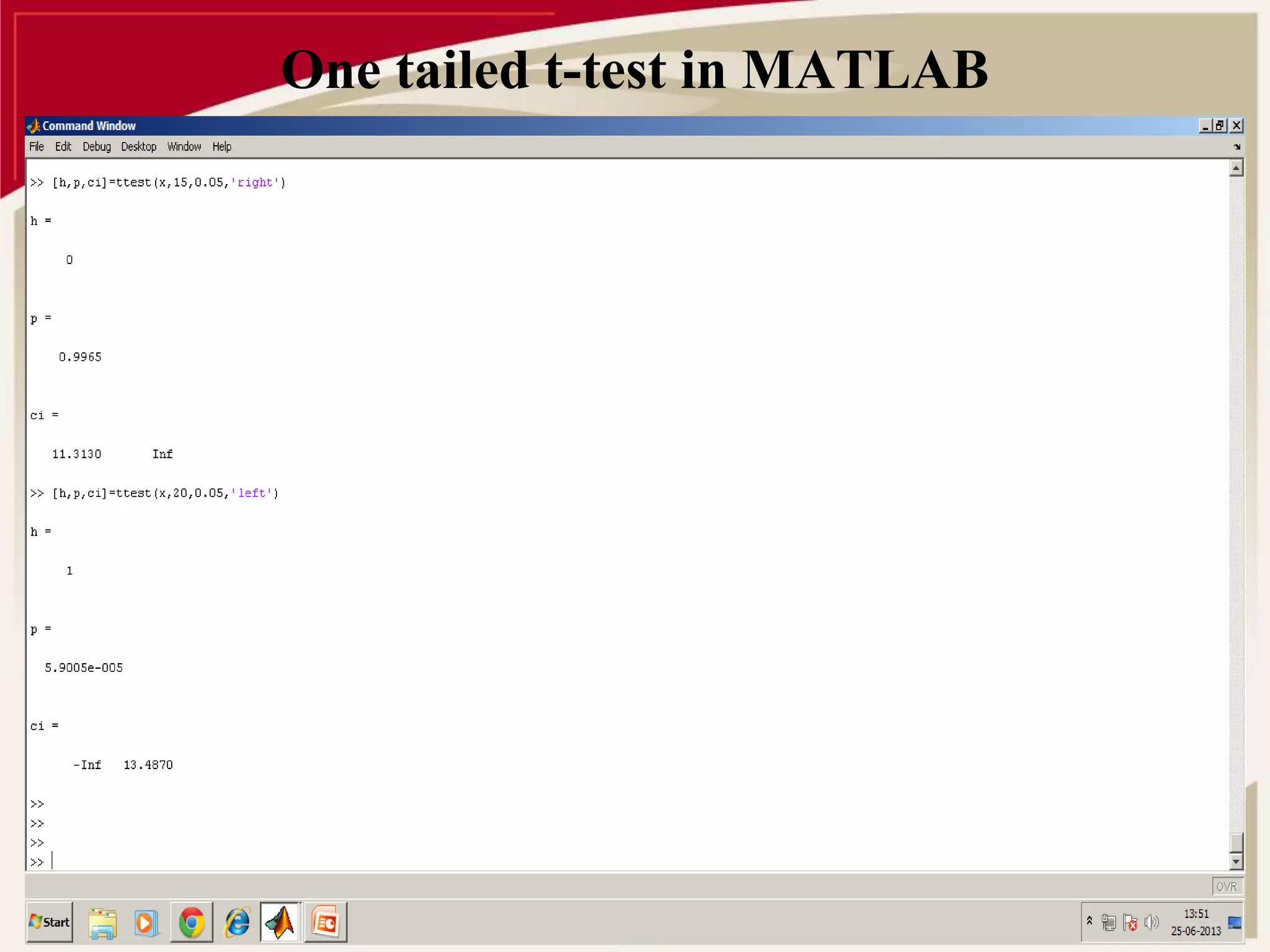
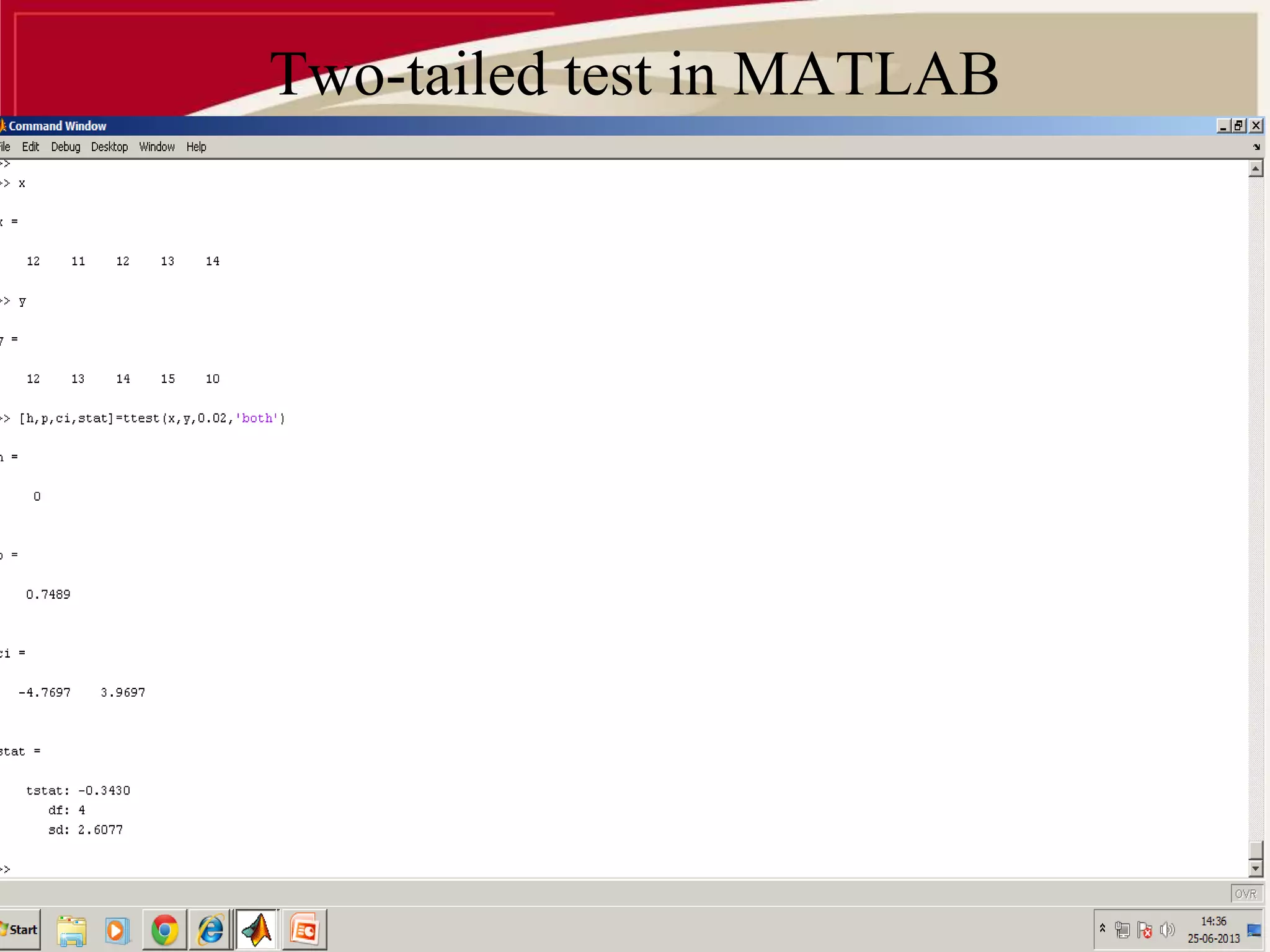
![t-test with own significance level:
[h,p,ci,stat] = TTEST(...,ALPHA) performs the test at the significance level
(100*ALPHA)%. ALPHA must be a scalar.](https://image.slidesharecdn.com/parametrictest-141109021327-conversion-gate01/75/Parametric-test-15-2048.jpg)