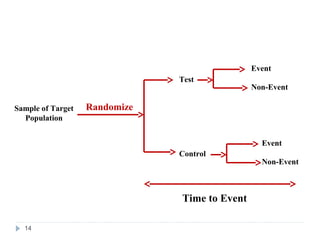
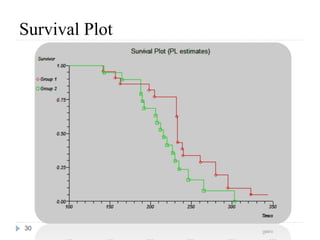
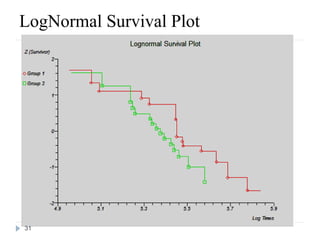
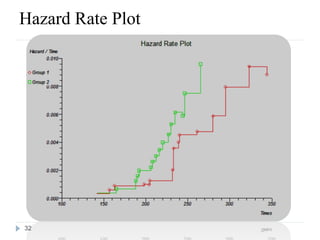
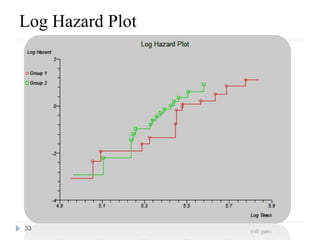
The document discusses survival analysis and Cox regression for cancer clinical trials. It begins with an overview of clinical trials for cancer, noting their complexity, long duration, high costs, and ethical concerns. It then covers survival analysis, describing key concepts like survival curves, hazard functions, and the Kaplan-Meier method for estimating survival when there is censoring. The document provides an example of survival data from a cancer study and discusses assumptions and parameters used in survival analysis like median and mean survival times.

1. Survival Analysis and Cox
Regression for Cancer Trials
Presented at PG Department of Statistics,
Sardar Patel University January 29, 2013
Dr. Bhaswat S. Chakraborty
Sr. VP & Chair, R&D Core Committee
Cadila Pharmaceuticals Ltd., Ahmedabad
1

2. Part 1: Survival Analysis of
Cancer CTs
2

3. Clinical Trials
 Organized scientific efforts to get direct answers from
relevant patients on important scientific questions on
(doses and regimens of) actions of drugs (or devices or
other interventions).
 Questions are mainly about differences or null
 Modern trials (last 40 years or so) are large, multicentre,
often international and co-operative endeavors
 Ideally, primary objectives are consistent with mechanism
of action
 Results can be translated to practice
 Would stand the regulatory and scientific scrutiny
3

4. Cancer Trials (Phases I–IV)
 Highly complex trials involving cytotoxic drugs, moribund patients,
time dependent and censored variables
 Require prolonged observation of each patient
 Expensive, long term and resource intensive trials
 Heterogeneous patients at various stages of the disease
 Prognostic factors of non-metastasized and metastasized diseases are
different
 Adverse reactions are usually serious and frequently include death
 Ethical concerns are numerous and very serious
 Trial management is difficult and patient recruitment extremely
challenging
 Number of stopped trials (by DSMB or FDA) is very high
 Data analysis and interpretation are very difficult by any standard
5

5. 6
Source: WHO

6. 7

7. India: 2010
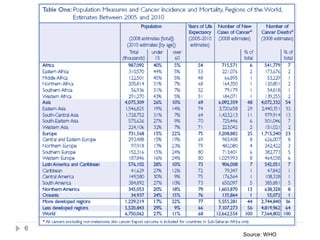
 7137 of 122 429 study deaths were due to cancer, corresponding to 556 400 national
cancer deaths in India in 2010.
 395 400 (71%) cancer deaths occurred in people aged 30—69 years (200 100 men
and 195 300 women).
 At 30—69 years, the three most common fatal cancers were oral (including lip and
pharynx, 45 800 [22·9%]), stomach (25 200 [12·6%]), and lung (including trachea
and larynx, 22 900 [11·4%]) in men, and cervical (33 400 [17·1%]), stomach
(27 500 [14·1%]), and breast (19 900 [10·2%]) in women.
 Tobacco-related cancers represented 42·0% (84 000) of male and 18·3% (35 700) of
female cancer deaths and there were twice as many deaths from oral cancers as lung
cancers.
 Age-standardized cancer mortality rates per 100 000 were similar in rural (men 95·6
[99% CI 89·6—101·7] and women 96·6 [90·7—102·6]) and urban areas (men 102·4
[92·7—112·1] and women 91·2 [81·9—100·5]), but varied greatly between the
states.
 Cervical cancer was far less common in Muslim than in Hindu women (study deaths
24, age-standardized mortality ratio 0·68 [0·64—0·71] vs 340, 1·06 [1·05—1·08]).
8

8. 10

9. Survival Analysis
 Survival analysis is studying the time between entry
to a study and a subsequent event (such as death).
 Also called “time to event analysis”
 Survival analysis attempts to answer questions such
as:
 which fraction of a population will survive past a certain
time ?
 at what rate will they fail ?
 at what rate will they present the event ?
 How do particular factors benefit or affect the probability of
survival ?
11

10. What kind of time to event data?
 Survival Analysis typically focuses on time to event data.
 In the most general sense, it consists of techniques for
positive-valued random variables, such as
 time to death
 time to onset (or relapse) of a disease
 length of stay in a hospital
 money paid by health insurance
 viral load measurements
 Kinds of survival studies include:
 clinical trials
 prospective cohort studies
 retrospective cohort studies
 retrospective correlative studies
12

11. Definition and Characteristics of Variables
 Survival time (t) random variables (RVs) are always non-
negative, i.e., t ≥ 0.
 T can either be discrete (taking a finite set of values, e.g.
a1, a2, …, an) or continuous [defined on (0,∞)].
 A random variable t is called a censored survival time RV
if x = min(t, u), where u is a non-negative censoring
variable.
 For a survival time RV, we need:
 (1) an unambiguous time origin (e.g. randomization to clinical
trial)
 (2) a time scale (e.g. real time (days, months, years)
 (3) defnition of the event (e.g. death, relapse)
13

12. Event
Test
Non-Event
Sample of Target Randomize
Population
Event
Control
Non-Event
Time to Event
14

13. Illustration of Survival Data
15

14. Characterization of Survival
 There are several equivalent ways to characterize the
probability distribution of a survival random variable.
 We will use the following terms:
 The density function f(t)
 The survival or survivor function S(t)
 The hazard function H(t)
 The cumulative hazard function Λ(t)
 Median survival, called τ, is defined as
 S(τ ) = 0.5
 Similarly, any other percentiles could be defined
Practically, we estimate median survival as the smallest
time τ such that
 Ŝ (τ) ≤ 0.5
16

15. Estimation of Survival Function from
Censored Data
 Hazard shapes can be increasing (e.g. aging after 65),
decreasing (e.g. survival after surgery), bathtub (e.g. age-
specifc mortality) or constant (e.g. survival of patients with
advanced chronic disease)
 If there are censored observations, then Ŝ(t) by a parametric
method is not a good estimate of the true S(t), so non-
parametric methods must be used to account for censoring
(life-table methods, Kaplan-Meier estimator)
 Kaplan-Meier estimator is the most popular
 However, theoretically (or when conditions are met) survival
data can be fit to parametric models as well
17

16. 18
Source: Ibrahim J (2005), Amer Stat Assoc

17. Survival Rate by Kaplan Meier
 This function estimates survival rates and hazard from data that may be incomplete.
The survival rate is expressed as the survivor function (S):
 where t is the survival time
 e.g. 2 years in the context of 5 year survival rates
 Sometimes S is estimated as the probability of surviving to time t for those alive just
before t multiplied by the proportion of subjects surviving to t
 Calculated by product limit (PL) method 1 or the simpler Nelson-Aalen estimate2,
estimate of which is always less than a Peterson estimate
Peterson PL Method Nelson-Aalen Method
 where ti is duration of study at point i, di is number of deaths up to point i and ni is
number of individuals at risk just prior to ti.
19

18. Data
 Following example is data of death from a cancer after
exposure to a particular carcinogen in two groups of patients.
 Group 1 had a different pre-treatment régime to group 2
 The time from pre-treatment to death is recorded.
 If a patient was still living at the end of the experiment or it
had died from a different cause then that time is considered
censored (* below). A censored observation is given the value
0 in the death/censorship variable to indicate a "non-event".
 Group 1: 143, 165, 188, 188, 190, 192, 206, 208, 212, 216, 220, 227, 230,
235, 246, 265, 303, 216*, 244*
 Group 2: 142, 157, 163, 198, 205, 232, 232, 232, 233, 233, 233, 233, 239,
240, 261, 280, 280, 295, 295, 323, 204*, 344*
20

19. Assumptions
 S is based upon the probability that an individual survives at
the end of a time interval, on the condition that the individual
was present at the start of the time interval. S is the product (P)
of these conditional probabilities.
 If a subject is last followed up at time ti and then leaves the study for any reason
(e.g. lost to follow up) ti is counted as their censorship time.
 Censored individuals have the same prospect of survival as
those who continue to be followed. This can not be tested for
and can lead to a bias that artificially reduces S.
 Survival prospects are the same for early as for late recruits to
the study (can be tested for).
 The event studied (e.g. death) happens at the specified time.
Late recording of the event studied will cause artificial
inflation of S.
21

20. Other Parameters
 The cumulative hazard function (H) is the risk of event 2 (e.g. death) at time t
 S and H with their standard errors and confidence intervals need to be saved
 Median and mean survival time
 The median survival time is calculated as the smallest survival time for which the survivor
function is less than or equal to 0.5.
 Some data sets may not get this far, in which case their median survival time is not
calculated.
 A confidence interval for the median survival time can be constructed using a robust non-
parametric method or using a large sample estimate of the density function of the survival
estimate
 Mean survival time is estimated as the area under the survival curve. The estimator is based
upon the entire range of data
 Some software uses only the data up to the last observed event; this biases the estimate of
the mean downwards, entire range of data should be used
 Samples of survival times are frequently highly skewed, therefore, in survival analysis, the
median is generally a better measure of central location than the mean
22

21. Variances of S & H hat
 The variance of S
 The confidence interval for the survivor function is not calculated directly using
Greenwood's variance estimate as this would give impossible results (< 0 or > 1) at
extremes of S. The confidence interval for S uses an asymptotic maximum likelihood
solution by log transformation
 The variance of H hat is estimated as:
23

22. Cancer Trial Data Preparation
 Data is very complex, statistical skills & insight are necessary
 Time-to-event:
 time a patient in a trial survived
 time to tumor progression or relapse in a patient
 Event / censor code: 1 or 0
 1 for event(s) happened
 0 for no event or lost to follow up but survival assumed
 Stratification:
 e.g. centre code for a multi-centre trial
 Be careful with your choice of strata
 Predictors (covariates):
 which can be a number of variables that are thought to be related to the
event under study, e.g., drug treatment, disease stage
24

23. Organized Input Data
Group Surv Time Surv Censor Surv Group Surv Time Surv Censor Surv
2 142 1 2 232 1
1 143 1 2 232 1
2 157 1 2 232 1
2 163 1 2 233 1
1 165 1 2 233 1
1 188 1 2 233 1
2 233 1
1 188 1 1 235 1
1 190 1 2 239 1
1 192 1 2 240 1
2 198 1 1 244 0
2 204 0 1 246 1
2 205 1 2 261 1
1 206 1 1 265 1
1 208 1 2 280 1
1 212 1 2 280 1
1 216 0 2 295 1
1 216 1 2 295 1
1 220 1 1 303 1
1 227 1 2 323 1
1 230 1 2 344 0
25

24. Analyzed K-M Survival Group 1 (Life
Table)
Time At risk Dead Censore S SE(S) H SE(H)
d
143 19 1 0 0.947368 0.051228 0.054067 0.054074
165 18 1 0 0.894737 0.070406 0.111226 0.078689
188 17 2 0 0.789474 0.093529 0.236389 0.118470
190 15 1 0 0.736842 0.101023 0.305382 0.137102
192 14 1 0 0.684211 0.106639 0.37949 0.155857
206 13 1 0 0.631579 0.110665 0.459532 0.175219
208 12 1 0 0.578947 0.113269 0.546544 0.195646
212 11 1 0 0.526316 0.114549 0.641854 0.217643
216 10 1 1 0.473684 0.114549 0.747214 0.241825
220 8 1 0 0.414474 0.114515 0.880746 0.276291
227 7 1 0 0.355263 0.112426 1.034896 0.316459
230 6 1 0 0.296053 0.108162 1.217218 0.365349
235 5 1 0 0.236842 0.10145 1.440362 0.428345
244 4 0 1 0.236842 0.10145 1.440362 0.428345
246 3 1 0 0.157895 0.093431 1.845827 0.591732
265 2 1 0 0.078947 0.072792 2.538974 0.922034
26 303 1 1 0 0 * infinity *

25. Descriptive Stats Group 1
 Median survival time = 216
 Andersen 95% CI for median survival time = 199.62 to
232.382
 Brookmeyer-Crowley 95% CI for median survival time = 192
to 230

 Mean survival time (95% CI) = 218.68 (200.36 to 237.00)
27

26. Analyzed K-M Survival Group 2 (Life
Table)
Time At risk Dead Censored S SE(S) H SE(H)
142 22 1 0 0.954545 0.044409 0.04652 0.046524
157 21 1 0 0.909091 0.061291 0.09531 0.06742
163 20 1 0 0.863636 0.073165 0.146603 0.084717
198 19 1 0 0.818182 0.08223 0.200671 0.100504
204 18 0 1 0.818182 0.08223 0.200671 0.100504
205 17 1 0 0.770053 0.090387 0.261295 0.117378
232 16 3 0 0.625668 0.105069 0.468935 0.16793
233 13 4 0 0.433155 0.108192 0.836659 0.249777
239 9 1 0 0.385027 0.106338 0.954442 0.276184
240 8 1 0 0.336898 0.103365 1.087974 0.306814
261 7 1 0 0.28877 0.099172 1.242125 0.34343
280 6 2 0 0.192513 0.086369 1.64759 0.44864
295 4 2 0 0.096257 0.064663 2.340737 0.671772
323 2 1 0 0.048128 0.046941 3.033884 0.975335
28 344 1 0 1 0.048128 0.046941 3.033884 0.975335

27. Descriptive Stats Group 2
 Median survival time = 233
 Andersen 95% CI for median survival time = 231.89 to 234.10
 Brookmeyer-Crowley 95% CI for median survival time = 232
to 240
 Mean survival time (95% CI) = 241.28 (219.59 to 262.98)
29

28. Survival Plot
30

29. LogNormal Survival Plot
31

30. Hazard Rate Plot
32

31. Log Hazard Plot
33

32. Comparing Survival Functions
 Due to the censoring, classical tests such as t-test and
Wilcoxon test cannot be used for the comparison of the
survival times
 Various tests have been designed for the comparison of
survival curves, when censoring is present
 • The most popular ones are:
 Logrank (or Cox-Mantel or Mantel-Haenszel) test
 Wilcoxon (Gehan) test
 The Logrank test has more power than Wilcoxon for detecting
late differences
 The Logrank test has less power than Wilcoxon for detecting
early differences
 The logrank statistic is distributed as χ2 with a H0 that survival
functions of the two groups are the same
34

33. 35

34. Cox-Mantel Log Rank Test
Group Events observed Events expected
1 17 12.20368414
2 20 24.79631586
Degrees of
Chi-square Freedom P
3.124689787 1 0.077114564
The test statistic for equality of survival across the k groups
(populations sampled) is approximately chi-square distributed
on k-1 degrees of freedom.

35. Show the Excel Sheet
followed by Case Study
37

36. Case Study
• Purpose: This, the largest randomized study in pancreatic
cancer performed to date, compares marimastat, the first of
a new class of agents, with gemcitabine
• Context: The prognosis for unresectable pancreatic cancer
remains dismal (1-year survival rate, < 10%; 5-year
survival rate, < 5%)
– Recent advances in conventional chemotherapy and novel
molecular treatment strategies warrant investigation
38

37. Case Study: Patients
• Histologically or cytologically proven adenocarcinomas of the pancreas
– unresectable on computed tomographic imaging
• Tumors were staged
– Using the International Union Against Cancer tumor-node-metastasis classification
– Stage-grouped according to the American Joint Committee on Cancer Staging criteria for
pancreatic cancer
• Inclusion Criteria
– Patients entered the study within 8 wks of initial diagnosis or within 8 weeks of recurrence after
prior surgery
– >18 years
– Karnofsky performance status (KPS) of at least 50%
– At entry, patients had to have adequate bone marrow reserves, defined 1,000/µL of
granulocytes, platelet 100,000/µL, and Hb 9 g/dL.
– Adequate baseline hepatic function (bilirubin 2 x ULN; AST, ALT, or alkaline phosphatase 5 x
ULN)
– Adequate renal function (creatinine 2 x ULN)
• Exclusion Criteria
– Any fprevious systemic anticancer therapy as a primary intervention for locally advanced or
metastatic disease
– Prior exposure to a metalloproteinase inhibitor or gemcitabine
– Patients with prior adjuvant or consolidation chemotherapy or radiotherapy and relapsed within
6 months after therapy
– Pregnant or lactating patients were excluded
– Patients who had other investigational agents within 4 weeks before study start
39

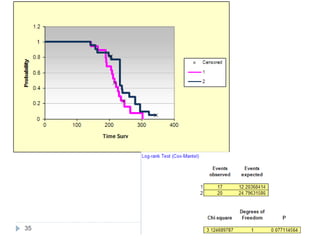
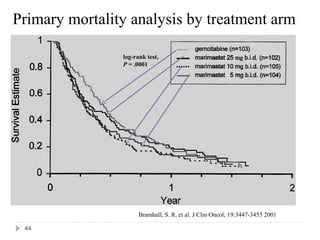
38. Case Study: End Points
• The primary study end point
– Overall survival, along with prospectively defined comparisons
between gemcitabine and marimastat 25 mg bid and between
gemcitabine and marimastat 10 mg bid
– Secondary study end points
• Progression-free survival
• Patient benefit s
– quality of life [QOL], weight loss, pain, analgesic consumption, surgical
intervention to alleviate cancer symptoms, and KPS)
• Safety and tolerability
• Tumor response rate was also assessed
40

39. Case Study: Randomization & Treatments
 Randomization
 IC obtained from each patient before study entry
 A computer-generated random code used according to the method of minimization. This
method balanced the treatment groups on the basis of stage of disease (stage I/II, III, or IV),
KPS (50% to 70% v 80% to 100%), sex, disease status (recurrent v newly diagnosed), and
study center.
 Patients received
 either 5 mg, 10 mg, or 25 mg of marimastat bid orally
 or 1,000 mg/m2 of gemcitabine hydrochloride by intravenous infusion
 The marimastat dosage was double-blinded but allocations to marimastat or gemcitabine
were open-label due to the different modes of administration
 Treatment
 Marimastat: 5 mg bid, 10 mg bid, or 25 mg bid with food. The dose of marimastat could be
reduced if musculoskeletal or other toxicities developed.
 Gemcitabine: 1,000 mg/m2 weekly for the first 7 weeks, no treatment in week 8, 1,000 mg/m2
weekly for 3 weeks next and nothing in the fourth week. Dose reduction (25%) permitted at
granulocyte 0.5-0.99/µL or platelet 50,000 to 99,999/µL
 If the counts were lower after the lower dose, the next dose was omitted.
 Patients who could not be treated for 6 weeks as a result of toxicity were withdrawn from the
study. No concomitant anticancer therapy
41

40. Case Study: Statistical Analysis
 Sample size (n= 400: 100 per group); based on absolute
differences in survival rates at 18 months of 14.5%, power of
80% and using a significance level of .025 (log-rank test,
Bonferoni adjusted)
• Also based on 10% survival rate at study censure with gemcitabine and a
mortality rate 75.5% in 10- or 25-mg marimastat groups
 Data Analysis
• Intent-to-treat -- Kaplan-Meier
• Cox proportional hazards model to identify prognostic factors and to explore their
influence on the comparative hazard of death between the treatment groups
• Plots of Log (-Log, survivor function) versus time for each individual variable
were produced to ensure proportional hazard assumptions were met
• In all survival analyses, patients who were lost to follow-up were censored at
their last known date alive.
• Proportions were tested using the χ2 test. Patient benefit data were tested using the
Wilcoxon rank sum test, and repeated measures analysis was applied to the QOL
data.
42

41. 43

42. Primary mortality analysis by treatment arm
log-rank test,
P = .0001
Bramhall, S. R. et al. J Clin Oncol; 19:3447-3455 2001
44

43. Case Study: Results
 The 1-year survival rate:
 was 19% for the gemcitabine group and 20% for the marimastat 25-mg group (χ2
test, P = .86). The 1-year survival rate for both the 10-mg and 5-mg groups was
14%
 Progression-free survival:
 revealed a significant difference between the gemcitabine group and each of the
three marimastat treatment groups (log-rank test, P = .0001), with median
progression-free survivals of 115, 57, 59, and 56 days for gemcitabine,
marimastat 25-, 10-, and 5-mg groups, respectively
 Cox proportional hazards:
 Factors associated with increased mortality risk were male sex, poor KPS (< 80),
presence of liver metastases, high serum lactate dehydrogenase, and low serum
albumin.
 Adjusted for these variables, there was no statistically significant difference in
survival rates between patients treated with gemcitabine and marimastat 25 mg,
but patients receiving either marimastat 10 or 5 mg were found to have a
significantly worse survival rate than those receiving gemcitabine
45

44. 46

45. 47

46. 48

47. End of Part 1
Your ?s
49

48. References
1. Kaplan EL, Meier P. Nonparametric estimation from incomplete observations.
Journal of the American Statistical Association (1958); 53: 457-481
2. Peterson AV Jr.. Expressing the Kaplan-Meier estimator as a function of
empirical subsurvival functions. Journal of the American Statistical Association
(1977); 72: 854-858
3. Nelson W. Theory and applications of hazard plotting for censored failure data.
Technometrics (1972); 14: 945-966
4. Aalen OO. Non parametric inference for a family of counting processes. Annals
of Statistics 1978; 6: 701-726.
5. R. Peto et al. Design and analysis of randomized clinical trials requiring
prolonged observation of each patient. British Journal of Cancer (1977); 31: 1-
39.
50

49. Thank You Very Much
51