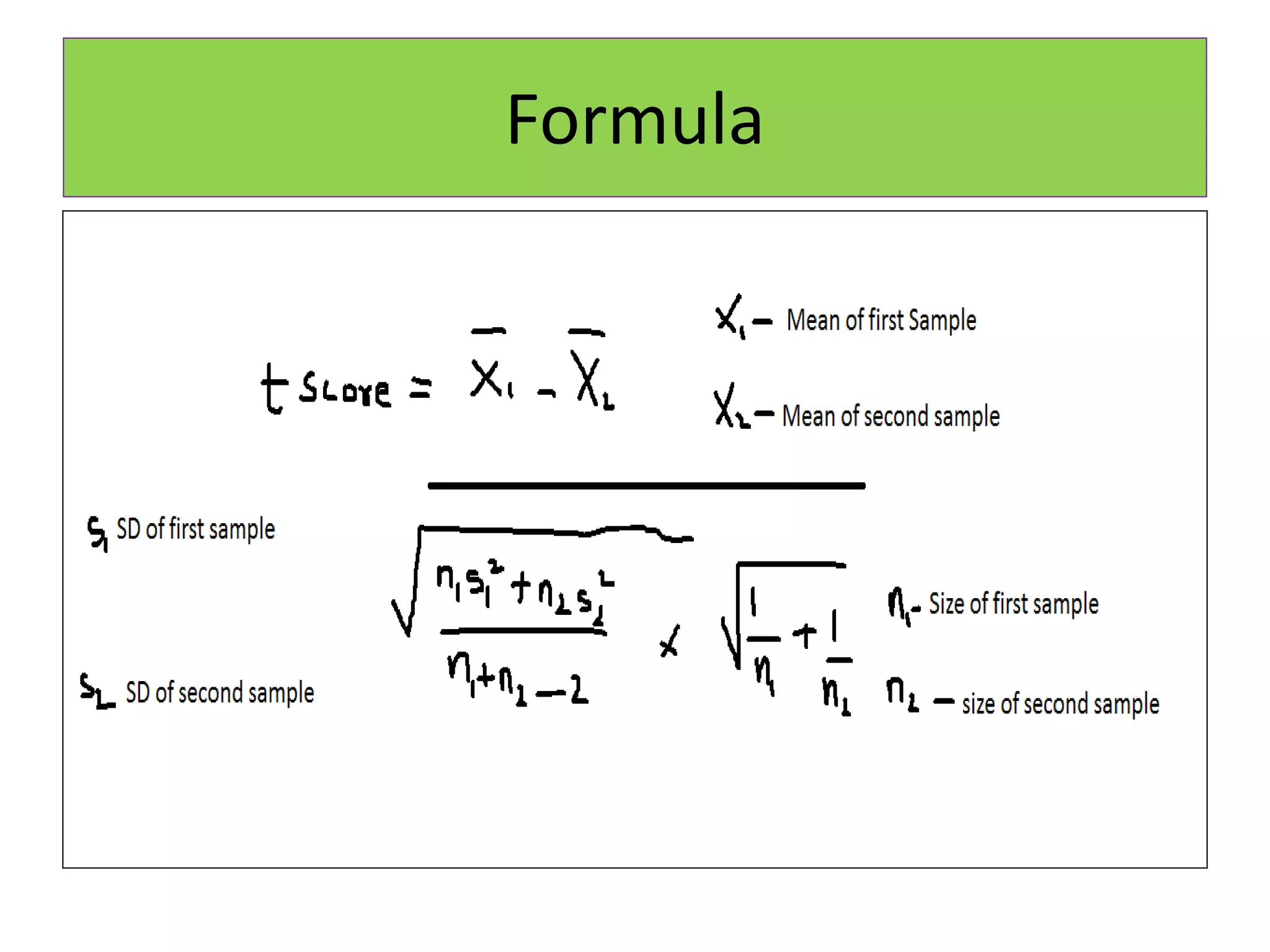
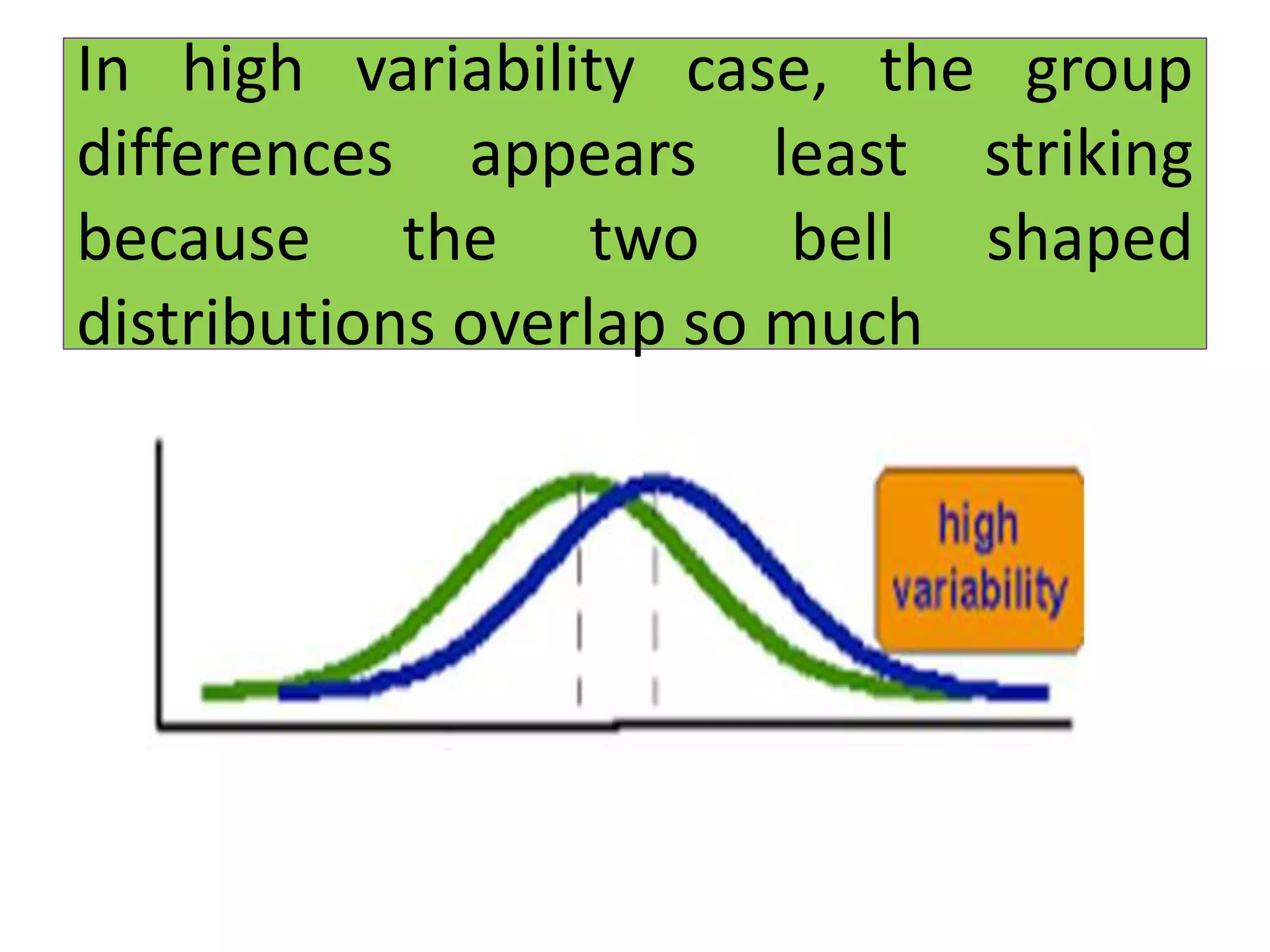
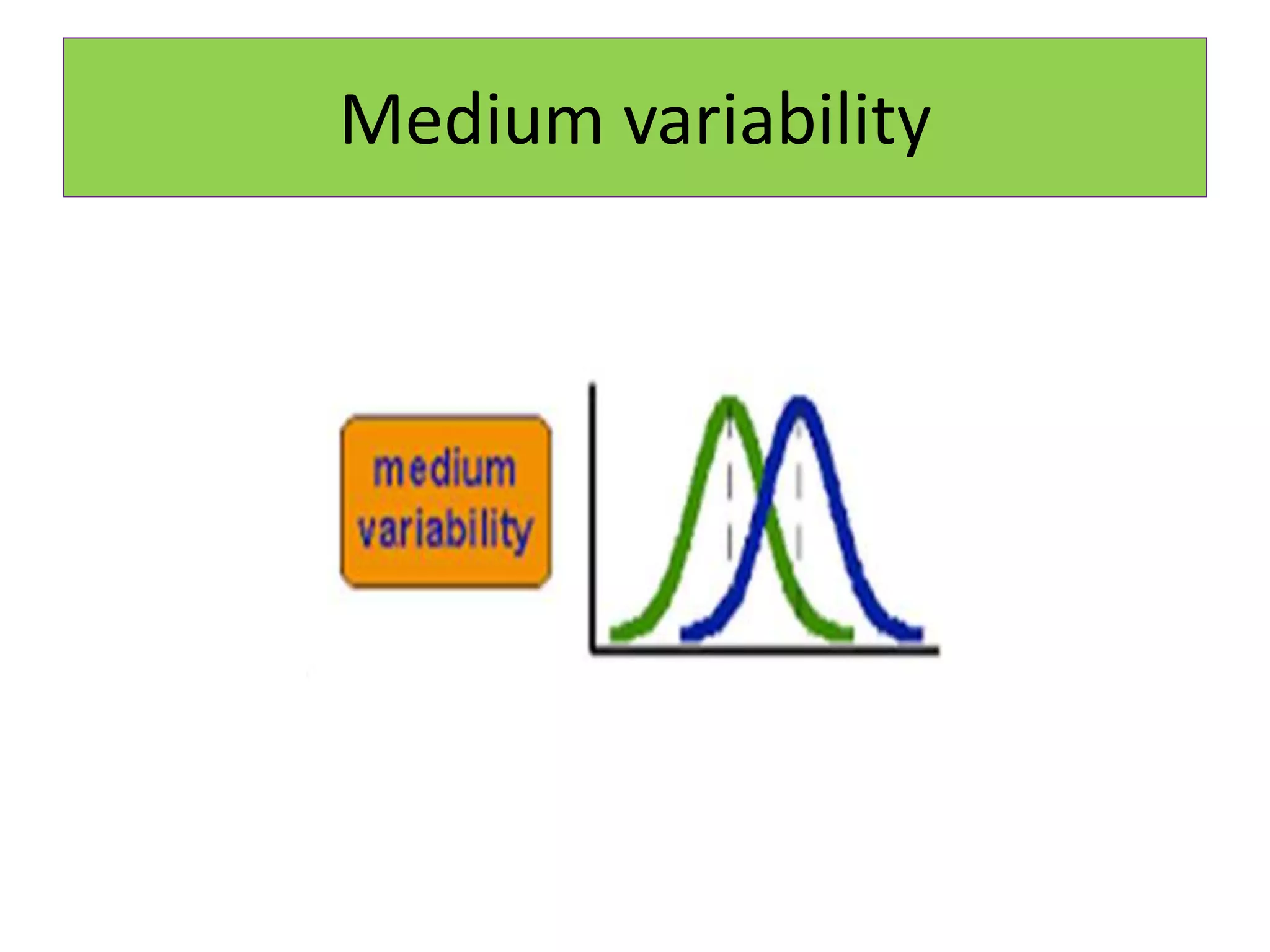
This document provides an overview of parametric statistical tests, including the z-test, t-tests, chi-square test, F-test, and Bartlett's test. It discusses the history and development of the Student's t-test, including its creation by William Gosset under the pseudonym "Student." The t-test is used to compare means between two samples or between a sample and a theoretical population. The document outlines the assumptions, calculations, and interpretations of one-sample, unpaired, and paired t-tests.

1. Parametric test

2. John
Arbuthnot
1667-1735
English statistician
First to use test of
significance

3. Outline of parametric test
Z test
Examines the null hypothesis that a
sample comes from normal
distribution with a known variance and
mean against the alternative
hypothesis that it does not have the
mean.

4. Student’s T test- one sample
It investigate the null hypothesis
that a sample comes from a
normal distribution with unknown
variance and a specified mean
against the alternative hypothesis
that it does not have the mean.

5. It examines whether two independent
samples come from normal
distributions with a unknown variance
and the same mean, against the
alternative hypothesis that the means
are equal.
Student’s T test- Two sample

6. CHI-SQUARE variance test
Test the null that a sample comes
from a normal distributions with a
specified variance against the
alternative hypothesis that it
comes from a normal distribution
with a different variance.

7. F - Test
Examines the null hypothesis that two
independent sample comes from
normal distribution with a same
variance against the alternative
hypothesis that they come from
normal distributions with different
variances.

8. BARTLETT’s test- Multiple –sample test
for equal variances.
It investigates the null hypothesis that multiple
samples come from normal distribution with a
same variance against the alternative hypothesis
that they come from normal distributions with
different variances.

9. Testing of hypothesis
It is of two type
Parametric test
Non parametric test

10. Parametric and non parametric test
Parametric test are more robust and
for the most part require less data to
make a stronger conclusion than non-
parametric test.
Non parametric is a statistical
procedure whereby the data does not
match a normal distribution.

11. Parameters of the population-
parametric
• Observation must be independent
• Observation must be drawn from normally
distributed population.
• Populations must have the same variance.
• Student t test is used when two independent
groups are compared.

12. Student ‘t’ test
• It is a statistical test which is commonly used
to compare the mean of two group of
samples.
• It is one of the most widely used parametric
test.
• It is a method of testing hypothesis about
mean of small sample drawn from a normally
distributed population when the standard
deviation for the sample is unknown.

13. Student ‘t’ test
Student ‘t’ test replaces
‘z’ test whenever the
standard deviation of the
population of the variable
is unknown.

14. Student ‘t’ test

15. History – Student ‘t’ test

16. William sealy Gosset 1876-1937
A british statistician
He work at Guinness
brewery in Dublin.
Guiness did not allow its
staff to publish.
So william used the pen
name ‘ Student ‘ .
The t- distribution was
published in 1905.

17. • He applied it in Quality control to
handle small samples in brewing.
• He applied statistical techniques
in agriculture to select the best-
yielding varieties of barley.
History – Student ‘t’ test

18. Problems due to small samples
• Wide variation in estimates from sample to
sample.
• When the sample size is small i.e less than 30,
the difference between the population
parameter and the sample static does not
follow the Gaussian or Normal distribution.

20. Student ‘t’ test
• As the sample size increases, the t-distribution
approximates the Gausian distribution.
• When sample size is 30 , the differences
between these distributions is very small.
• ‘t’ score is used for testing statistical
significance.
• The t curve is symmetrical but flatter than the
normal.

21. Degree of freedom
It is a number that
indicates the number of
values that can be
independently chosen.

22. The ‘t’ test assesses
whether the means of
two groups are
statistically different from
each other.
Student ‘t’ test

23. Two general research strategies
• Between subject design
• Two sets of data could come from two
independent populations
• Within subjects design
• Two sets of data could come from related
population

24. The figure shows where the control
and treatment group means are
located

25. The question that t test addresses is
whether the means are statistically
different

26. The difference between the mean is
same in all the three

27. You notice that three
situations don’t look
the same

28. There is a relatively little overlap
between the two bell shaped curves

29. In high variability case, the group
differences appears least striking
because the two bell shaped
distributions overlap so much

30. Medium variability

31. This lead us to an important
conclusion
• We are looking at the differences
between scores for two groups, we
have to judge the differences
between their means relative to the
spread or variability of their scores
• The t – test does just this

32. ‘t’ score

33. • The formula for the test is ratio.
• The top part of the ratio is just the
difference between the two means
or averages.
• The bottom part is a measure of the
variability or dispersion of the score.

34. • The formula is essentially another
example of the signal to noise
• The difference between the means is
signal and the bottom part is a
measure of variability that is
essentially noise.

35. The t value will be
positive if the first mean
is larger than the second
and negative if it is
smaller.

36. Problems
In a population the average weight of
males is 55 kg with a standard
deviation of 3 kg. A sample of 14
males was found to have a mean
weight of 60 kg. test at 5 % level of
significance whether the sample mean
is consistent with the population mean

37. Hypothesis
• Null hypothesis
• There is no difference between the sample
mean and population mean is 60 kg
• Alternative hypothesis
• The population mean is not 60 kg

38. As per null hypothesis
• Sample mean = 60 kg
• Population mean = 55 kg
• Population standard deviation = 3 kg
• Sample size is 14

39. Solution

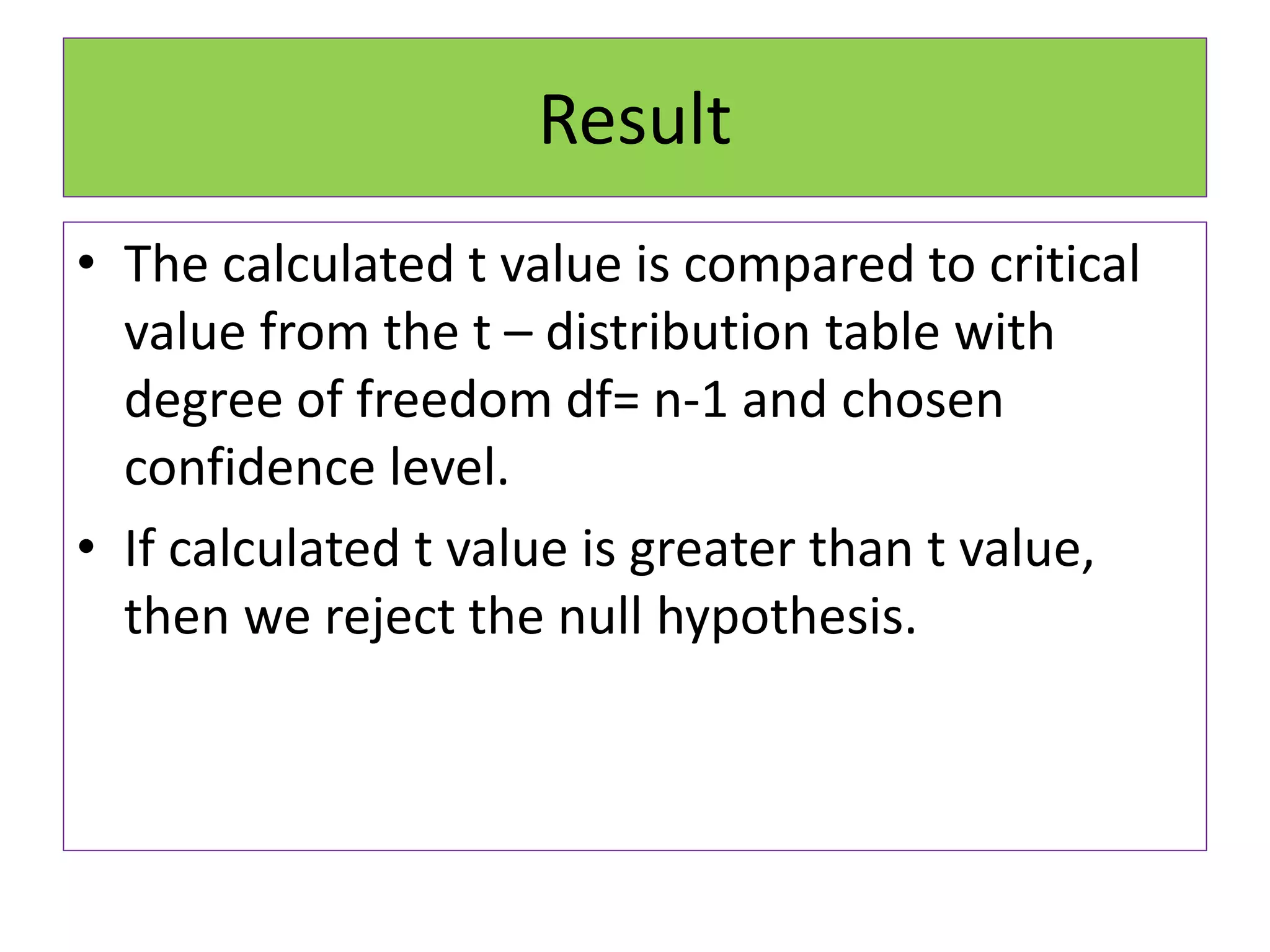
40. • For a two tailed test with df 13 at 5 % level of
significance the table value of ‘t’ test = t 0.05
13 = 2.160
• The t score is 6.2352 which is greater than
2.160
• Hence H0 is rejected [null hypothesis]
• The inference is that the sample mean is
significantly differ from the population mean
at 5 % level of significance

41. Problem two – unpaired t test
• The body weights of males and females having
the same heights are depicted
Is there a statistically significant gender difference in body weight
test at 5 % and 1% level of significance.
Null hypothesis there is no difference between two sample mean

42. Formula

43. Types of ‘t’ test
• One sample t test
• Two sample t test or unpaired t test
• Paired t test

44. One sample t test
• It is used to determine whether the mean of a
single variable differs from a specified
constant.
• Example
• Measure of a manufactured item are
compared against the required standard.
• Variable used in this test is known as test
variable.

46. • Degree of freedom = n1+ n2 -2 = 7+9-2 =14
• DF at 5 % level of significance, the table value
2.145
• T score 2.205 is greater than 2.145
• Ho is rejected

47. Inference at 1 % level of significance
• At DF = 14 at 1 % level of significance, the
table value at t = 2.977
• The t score is 2.205 is lesser than 2.977
• Ho is accepted
• The difference between the two sample mean
is statistically significant at 1 % level of
significant

48. One sample t test
The one sample t test compares a
sample mean to a hypothesized
population mean to determine
whether the two means are
significantly different.

49. Data for one sample t test requires
• Variables should be continuous and
independent of one another.
• Normal distribution of sample and population
on test variable.

50. Two types of hypothesis
• Null hypothesis
• Alternative hypothesis

51. X - sample mean
- Proposed constant for population mean
S- sample standard deviation
N- sample size

52. Result
• The calculated t value is compared to critical
value from the t – distribution table with
degree of freedom df= n-1 and chosen
confidence level.
• If calculated t value is greater than t value,
then we reject the null hypothesis.

53. Unpaired t test
• Unpaired t test is used to compare the mean of
two independent groups.
• In pharmaceutical research half of the subjects
are assigned to the treatment group and
remaining half subjects are randomly assigned to
control group.
• In research studies where two independent
groups eg women and men
• Unpaired t test is commonly used.it is most
widely used test in statistics.

54. Data should be
• Independent variables must consist of two
independent groups.
• Null hypothesis H0: there is no significant
difference between the means of two groups.
• Alternative hypothesis H1: there is a
significant difference between the two
population mean. This difference is unlikely to
be caused by sampling error or chance.

55. Paired t test
• It is used to compare two population means
where one sample can be paired with
observations in the other sample.
• It is repeated measures t test
• Before and after effect of a pharmaceutical
treatment on the same group of the people or
change in blood pressure before and after
treatment of hypertention.

56. • The difference between the before and after is
normally distributed