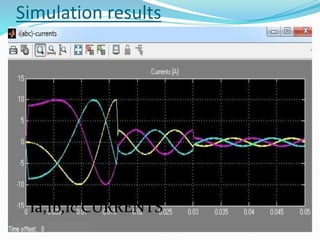
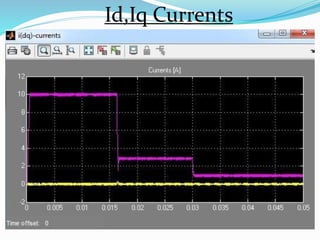
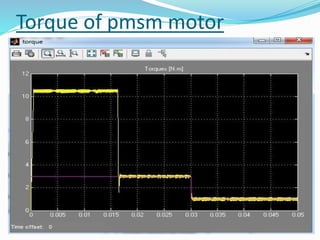
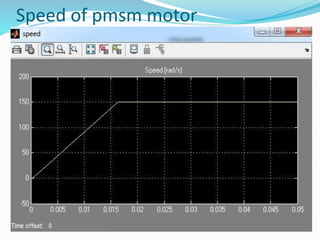
This document summarizes the modeling of a permanent magnet synchronous motor (PMSM) in Simulink. It describes how a PMSM is modeled in the rotor synchronous reference frame using Park equations. It discusses how the electromagnetic torque produced by the motor depends on the quadrature stator current. It also describes how the speed is controlled by controlling the electromagnetic torque through regulating the quadrature current. Finally, it presents the simulation results for the currents, torque, and speed of the modeled PMSM motor.

1. BIBHU PRASAD GANTHIA

2. Permanent Magnet Synchronous
Motor (PMSM)
 The PMSM is a brushless machine with sinusoidal
flux distribution, for which reason it is also known
as a brushless AC (BLAC) machine.
 In a PMSM the stator voltage must be sinusoidal.
The amplitude and frequency of the stator voltage
must be related to the rotor speed, and the
sinusoidal waveform must be in tune with the
rotor position.

3. Modeling of a PMSM in SIMULINK
The PMSM is usually modeled in the rotor
synchronous rotating frame (q/d frame). A three
phase PMSM is electrically described in the rotor
synchronous rotating frame by the following
equations (Park equations)
(Where Vq,Vd,iq,id are the stator voltage and current quadrature and
direct components, Rs is the stator resistance Lqs,Lds are the stator
quadrature and direct impedances, λm is the amplitude of the flux
linkages established by the rotor permanent magnet, and ωe is the
angular speed of the stator electromagnetic field. )

4.  The electromagnetic torque produced by the motor
is given by:
(2)
 where P is the number of rotor magnetic poles. If
the rotor is perfectly round, the quadrature and
direct impedances are equal, and in this case the
electromagnetic torque only depends on the
quadrature stator current.
 The mechanical equation of the motor is:
(3)

5.  where J is the rotor moment of inertia, TL is the load
torque, and F is the friction factor.
 As it can be observed in equation (4), the speed is
controlled by controlling the electromagnetic
torque. This, in turn, is controlled by controlling the
quadrature current, as it is indicated by (2). The
quadrature and direct currents are controlled by the
quadrature and direct applied voltages, according to
(1). It can be observed that cross-coupling appears
between the two axes currents. This cross-coupling
must be compensated in the controller.

6. The motor is fed by a three phase voltage source
inverter (VSI). The VSI is controlled using space
vector modulation (SVM) and the SVM algorithm is
applied directly to the α/β voltage components.

7.  The PI controllers were discretized using the Tustin
approximation, and are described in discrete time by
the equation:
 Where KI is the integral gain ,Kp is the proportional
gain, ε is the controller input, and u is the controller
output.
 The a/b/c to q/d transform consists of two consecutive
transforms, a/b/c to α/β and α/β to q/d:

8. The SVM algorithm was replaced at this stage of
simulation by an α/β to a/b/c transformation and
the three phase voltages were fed to the motor
model by means of SimPowerSystems controlled
voltage sources.

9. Simulation results
Ia,Ib,Ic CURRENTS

10. Id,Iq Currents

11. Torque of pmsm motor

12. Speed of pmsm motor

13. Conclusion
A novel holistic modeling of speed controller for PMSM
was presented, using
Matlab Simulink and System Generator. The approach
presented allows the modeling of
the controller and the controlled system in the same
environment.

14. Future work
 The classical PWM method is used to generate the
requested motor voltages. To
 improve the system performance in terms of torque
ripple, power quality and better DC
 voltage utilization, space vector modulation can be
employed. The speed is estimated by
 the measurement of the position. The speed
estimation can be improved by the use of
 Kalman lters

15. THANKYOU