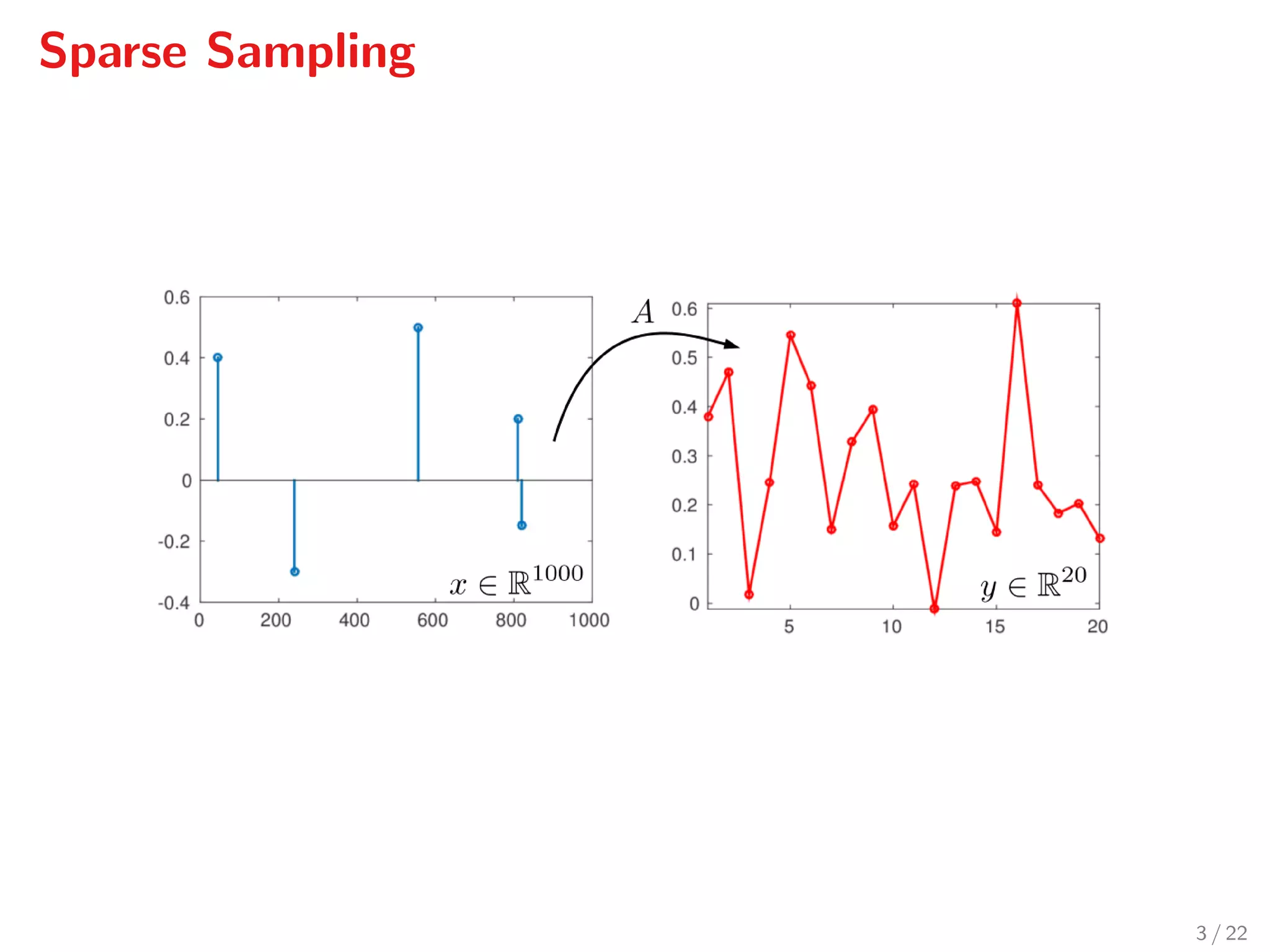
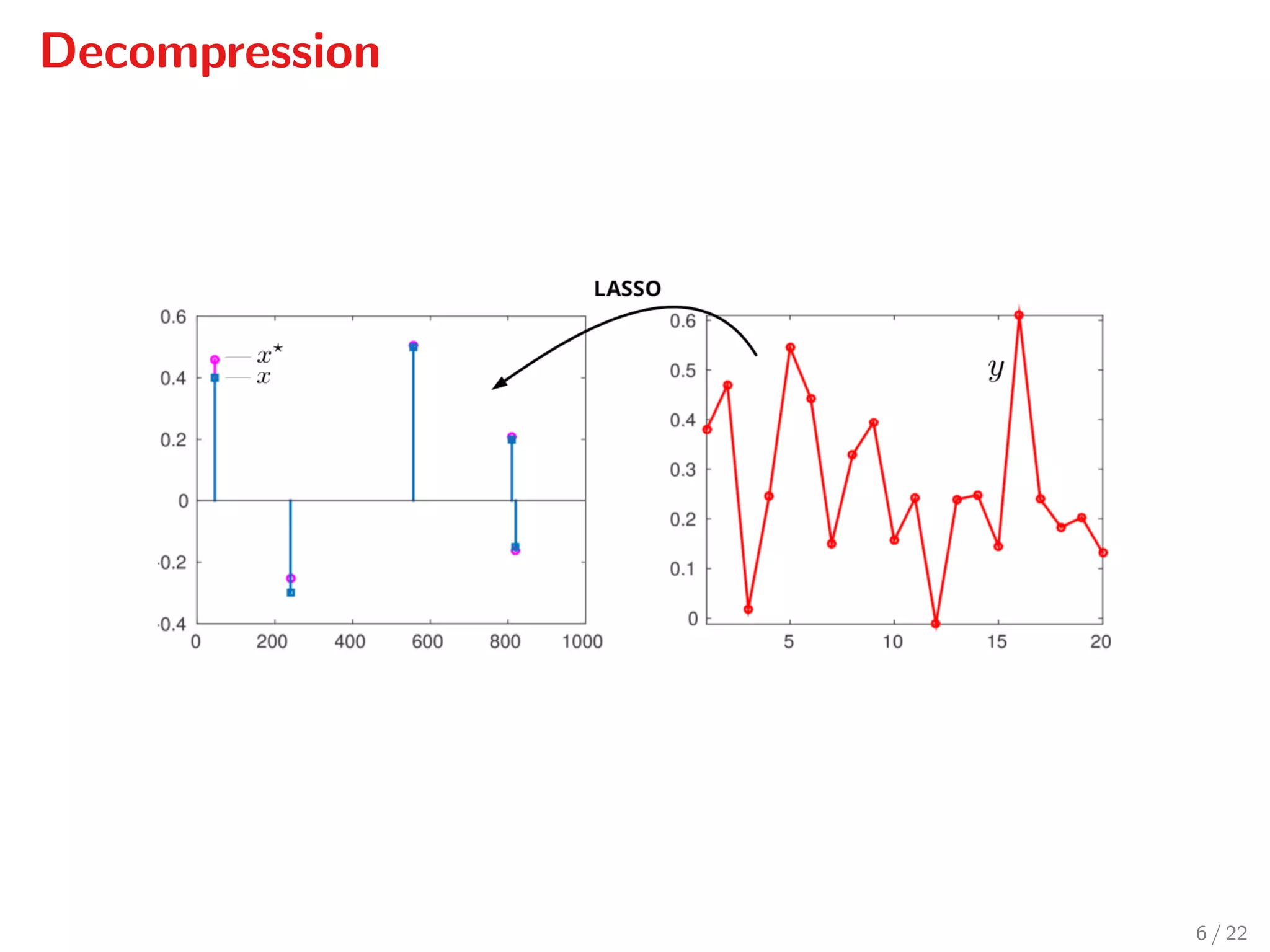
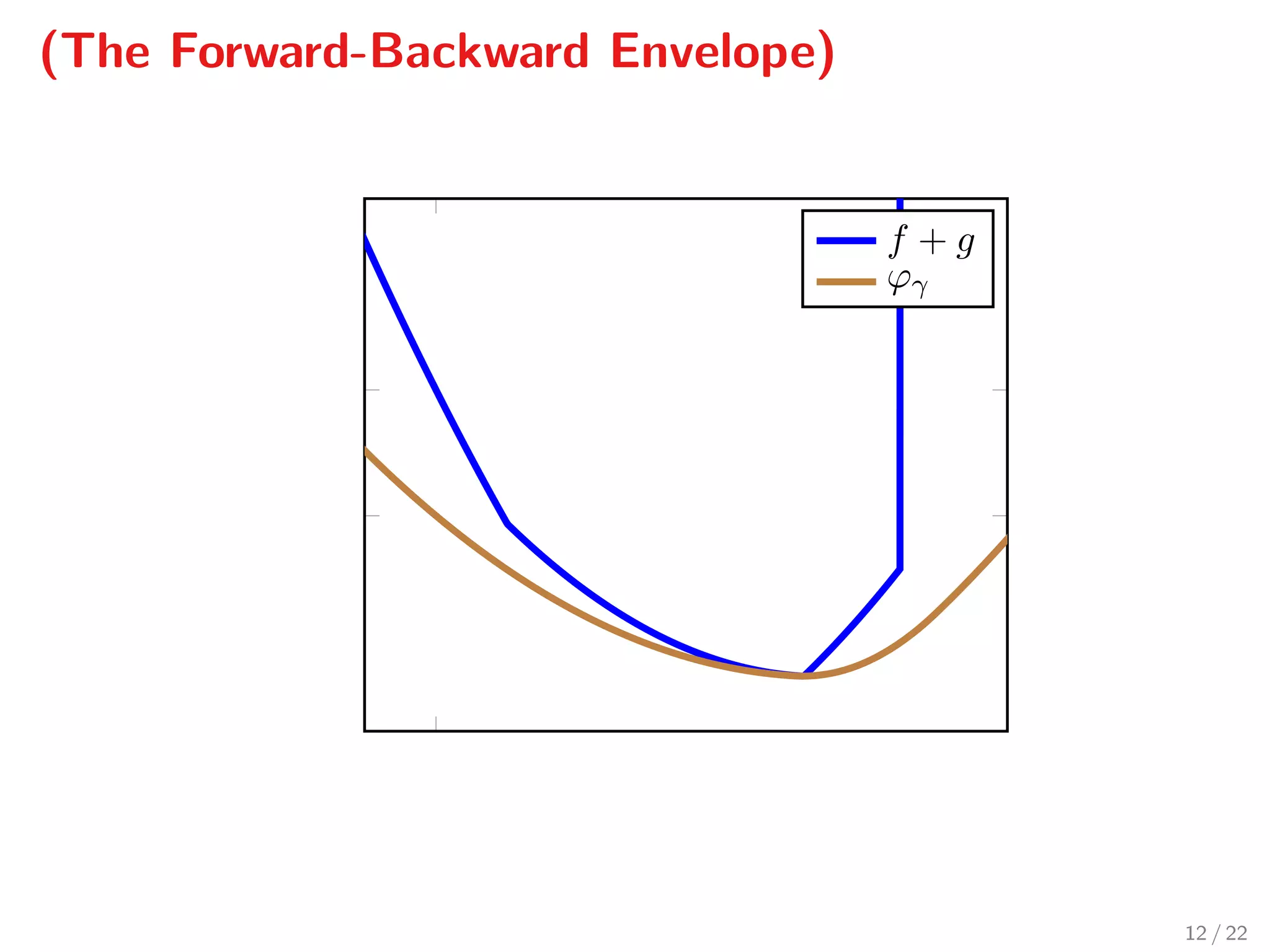
The document presents a novel methodology for accelerated reconstruction of compressively sampled data, achieving a speed that is an order of magnitude faster than existing recursive compressed sensing methods. It details the problem of retrieving sparse signals from noisy measurements, discusses the required properties of sampling matrices, and outlines the algorithmic approach using forward-backward Newton optimality conditions. Numerical simulations demonstrate the proposed method's significant performance advantages over traditional techniques like ISTA and FISTA.

1. Accelerated reconstruction of a compressively
sampled data stream
Pantelis Sopasakis∗,
Nikolaos Freris†, Panos Patrinos
∗ IMT School for Advanced Studies Lucca, Italy,
† NYU, Abu Dhabi, United Arab Emirates,
ESAT, KU Leuven, Belgium.
August 31, 2016

2. Contribution
The proposed methodology is an order of magnitude faster compared to
all state-of-the-art methods for recursive compressed sensing.
1 / 22

3. I. Recursive Compressed Sensing

4. Problem statement
Suppose a sparsely sampled signal y ∈ IRm
is produced by
y = Ax + w
where x ∈ IRn
(n m) is s-sparse and A is the sampling matrix and w
is a noise signal.
Problem. Retrieve x from y.
2 / 22

5. Sparse Sampling
3 / 22

6. Requirement
Matrix A must satisfy the restricted isometry property
(1 − δs) x 2
≤ Ax 2
≤ (1 + δs) x 2
,
for all x. A typical choice is a random A with entries drawn from
N(0, 1
m ) with m = 4s.
4 / 22

7. Decompression
Assuming
w ∼ N(0, σ2I)
the smallest element of |x| is not too small (> 8σ
√
2 ln n)
λ = 2σ
√
2 ln n
then, the LASSO solution
x = arg min
x
1
2
Ax − y 2
+ λ x 1,
and x have the same support whp.
5 / 22

8. Decompression
6 / 22

9. Recursive Compressed Sensing
Define
x(i)
= xi xi+1 · · · xi+n−1
Then x(i) produces the measured signal
y(i)
= A(i)
x(i)
+ w(i)
.
Sampling is performed with a fixed matrix A and
A(0)
= A
A(i+1)
= A(i)
P,
where P shifts the columns of A leftwards.
For details: Freris et al., 2014.
7 / 22

10. Recursive Compressed Sensing
Require: Steam of obsv, Window size n, Sparsity s, σ
λ ← 2σ
√
2 ln n, m ← 4s. Initialisation
Construct A with entries from N(0, 1
m )
A(0) ← A, x
(0)
◦ ← 0
for i = 0, 1, . . . do
1. Sample y(i)
2. Estimate support solving (initial guess: x
(i)
◦ ) LASSO
x
(i)
= arg min
1
2
A(i)
x − y(i) 2
+ λ x 1.
3. Perform debiasing on x
(i)
4. x
(i+1)
◦ ← P x
(i)
Warm Start
5. A(i+1) ← AP Permutation
end for
8 / 22

11. II. Forward-Backward Newton

12. Optimality Conditions
LASSO problem
minimise 1
2 Ax − y 2
f
+ λ x 1
g
Optimality conditions:
− f(x ) ∈ ∂g(x ),
with f(x) = A (Ax − y) and ∂g(x)i = λ sign(xi) for xi = 0,
∂g(x)i = [−λ, λ] for xi = 0, so
− if(x ) = λ sign(xi ), for xi = 0,
| jf(x )| ≤ λ, for xj = 0
9 / 22

13. Optimality Conditions
If we knew
α = {i : xi = 0},
β = {i : xi = 0}
then
Aα Aαxα = Aα y + λ sign(xα).
Goal. Devise a method to determine α efficiently.
10 / 22

14. Optimality Conditions
Write the optimality conditions as
x = proxγg(x − γ f(x )),
where
proxγg(z)i = sign(zi)(|zi| − γλ)+.
ISTA and FISTA are method for the iterative solution of these conditions.
Instead, we are looking for a zero of the fixed-point residual operator
Rγ(x) = x − proxγg(x − γ f(x)).
11 / 22

15. (The Forward-Backward Envelope)
x
ϕ(x)
ϕγ
f + g
ϕγ
12 / 22

16. (The Forward-Backward Envelope)
The forward-backward envelope is defined as
ϕγ(x) = min
z
f(x) + f(x) (z − x) + g(z) + 1
2γ z − x 2
In our case ϕγ is smooth with
ϕγ(x) = (I − γ 2
f(x))Rγ(x).
Key property.
arg min f + g = arg min ϕγ = zer ϕγ = zer Rγ
ϕγ is C1
but not C2
.
13 / 22

17. B-subdifferential
For a mapping F : IRn
→ IRn
which is almost-everywhere diff/ble, we
define its B-subdifferential to be
∂BF(x) := B ∈ IRn×n ∃{xν}ν : xν → x,
F (xν) exists, F (xν) → B
Facchinei & Pang, 2004.
14 / 22

18. Forward-Backward Newton
The proposed algorithm is
xk+1
= xk
− τkH−1
k Rγ(xk
),
Hk ∈ ∂BRγ(xk
).
When close to the solution all Hk are nonsingular. Take
Hk = I − Pk(I − γA A),
where P is diagonal with Pii = 1 iff i ∈ αk := {i : |xk
i − γ if(xk
i )| > γλ}.
The scalars τk are chosen by a simple line search algorithm to ensure global convergence.
15 / 22

19. The algorithm
... can be concisely written as
xk+1
= xk
+ τkdk
,
where dk is the solution of
dk
βk
= −(Rγ(xk
))βk
γAαk
Aαk
dk
αk
= −(Rγ(xk
))αk
− γAαk
Aβk
dk
βk
.
For global convergence we require
ϕγ(xk+1
) ≤ ϕγ(xk
) + ζτk ϕγ(xk) dk.
Converges locally quadratically; i.e., like exp(−ck2
).
16 / 22

20. Further acceleration
The algorithm can be further accelerated by
1. A continuation strategy (changing λ while solving)
2. Updating the Cholesky factorisation of Aα Aα
Please, see our paper for details.
17 / 22

21. III. Numerical Results

22. We are comparing the proposed method with
ISTA (or proximal gradient method)
FISTA (accelerated ISTA)
ADMM
L1LS
18 / 22

23. Simulations
For a 10%-sparse stream
Window size ×10 4
0.5 1 1.5 2
Averageruntime[s]
10 -1
10 0
10 1
FBN
FISTA
ADMM
L1LS
19 / 22

24. Simulations
For n = 5000 and different sparsities
Sparsity [%]
0 5 10 15
Averageruntime[s]
10 -1
10 0
FBN
FISTA
ADMM
L1LS
20 / 22

25. Conclusions
A semi-smooth Newton method for LASSO
Enabling very fast RCS
10 times faster than SoA algorithms
21 / 22

26. Thank you for your attention.
22 / 22