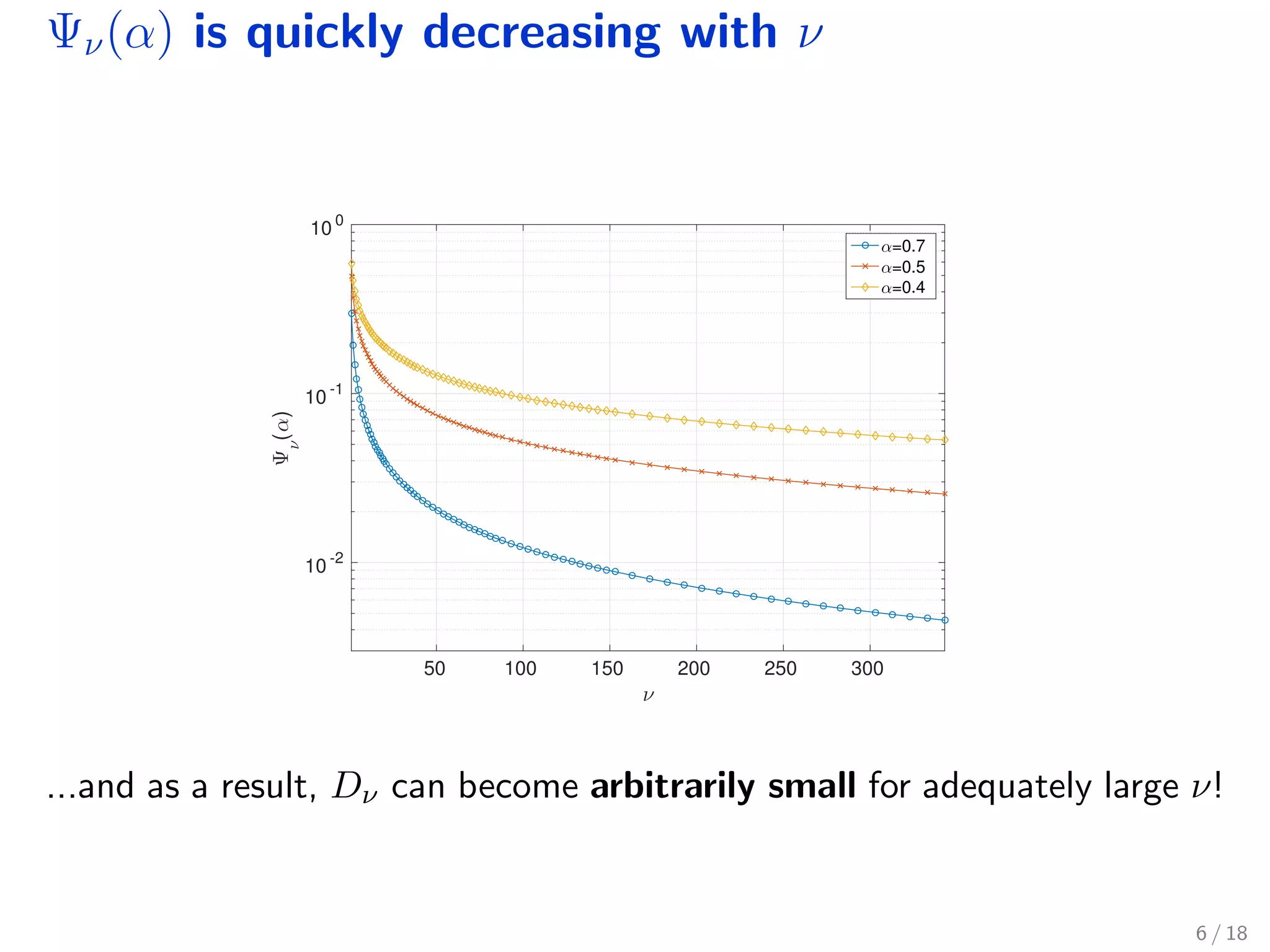
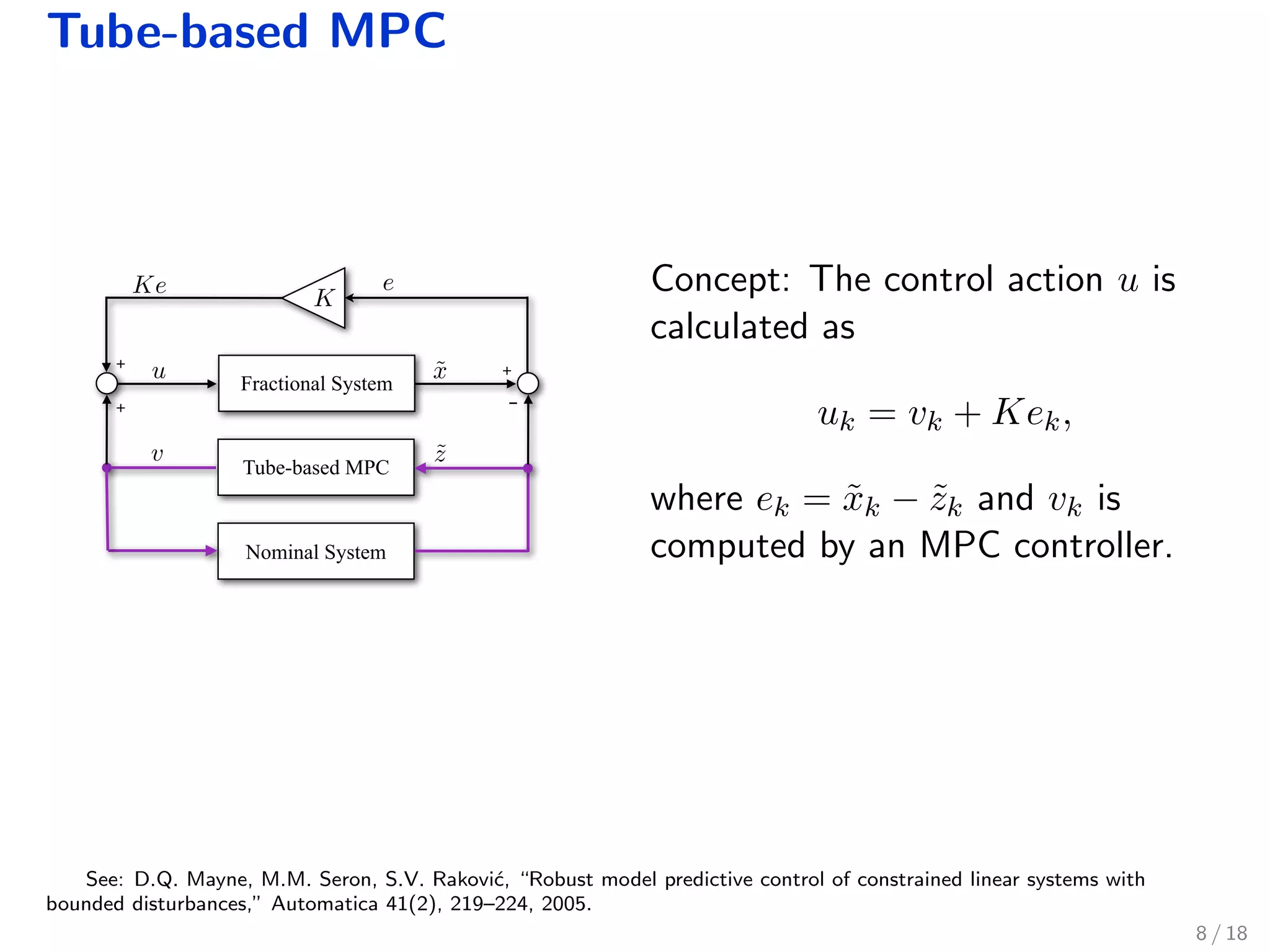
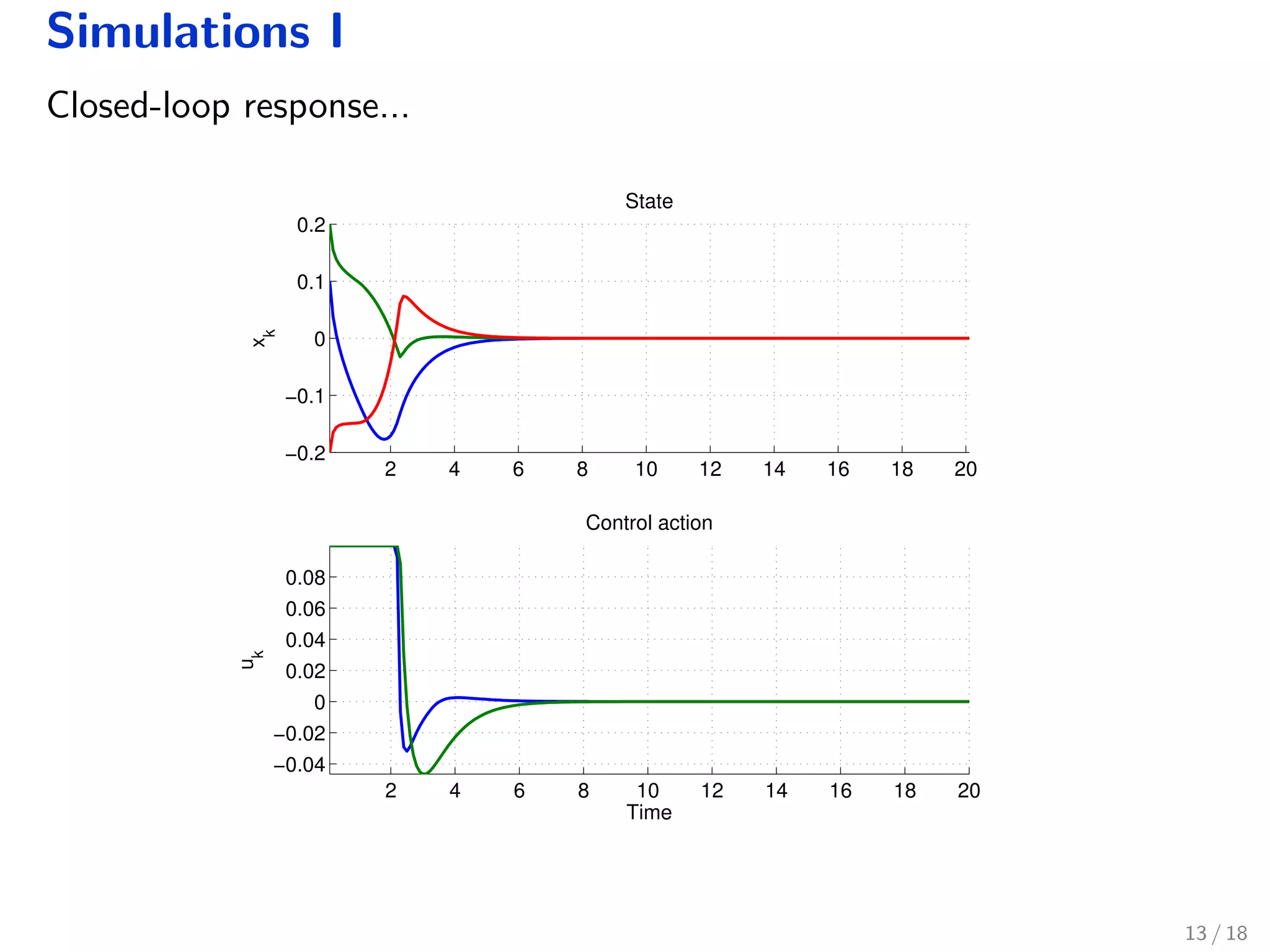
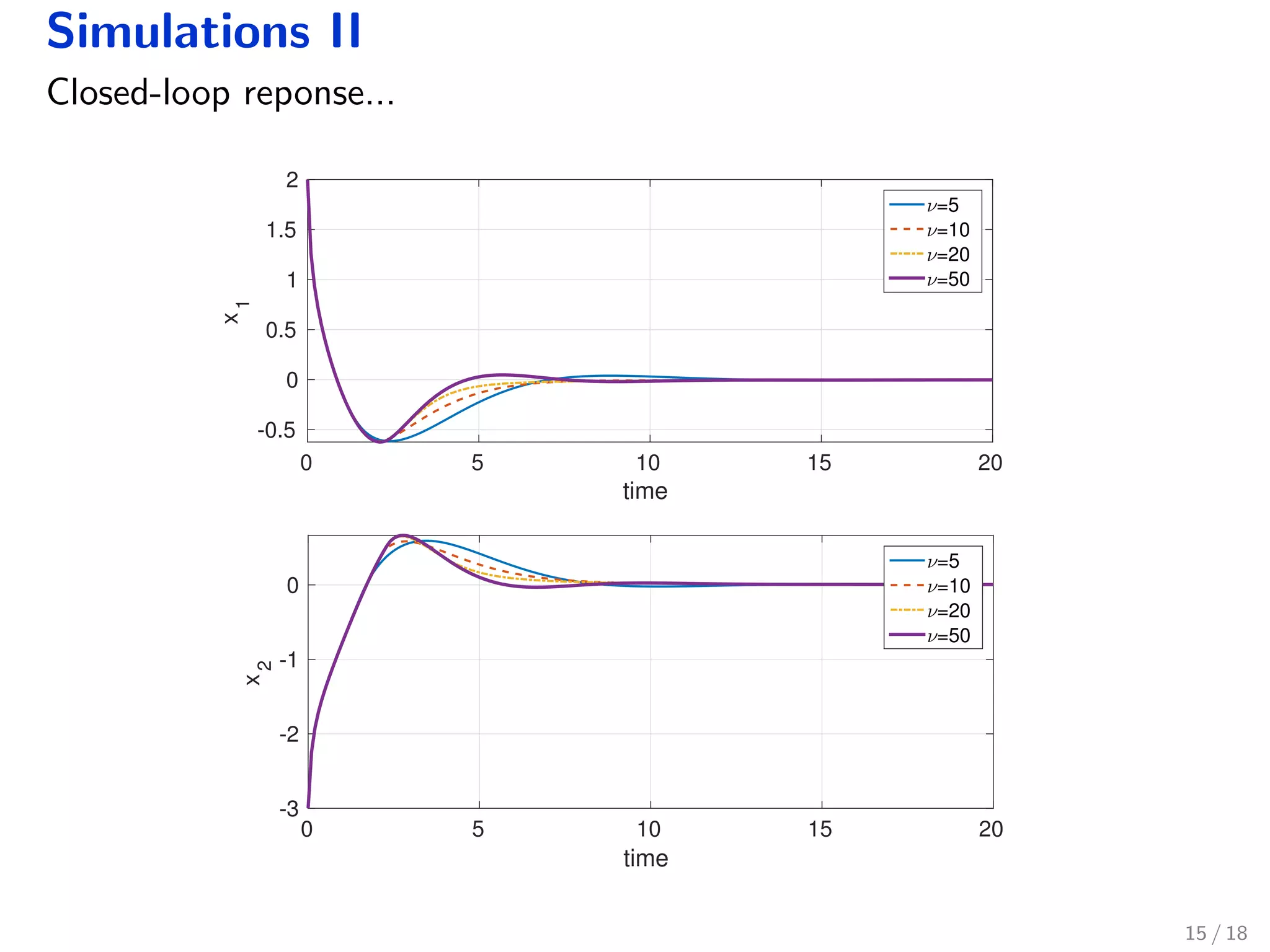
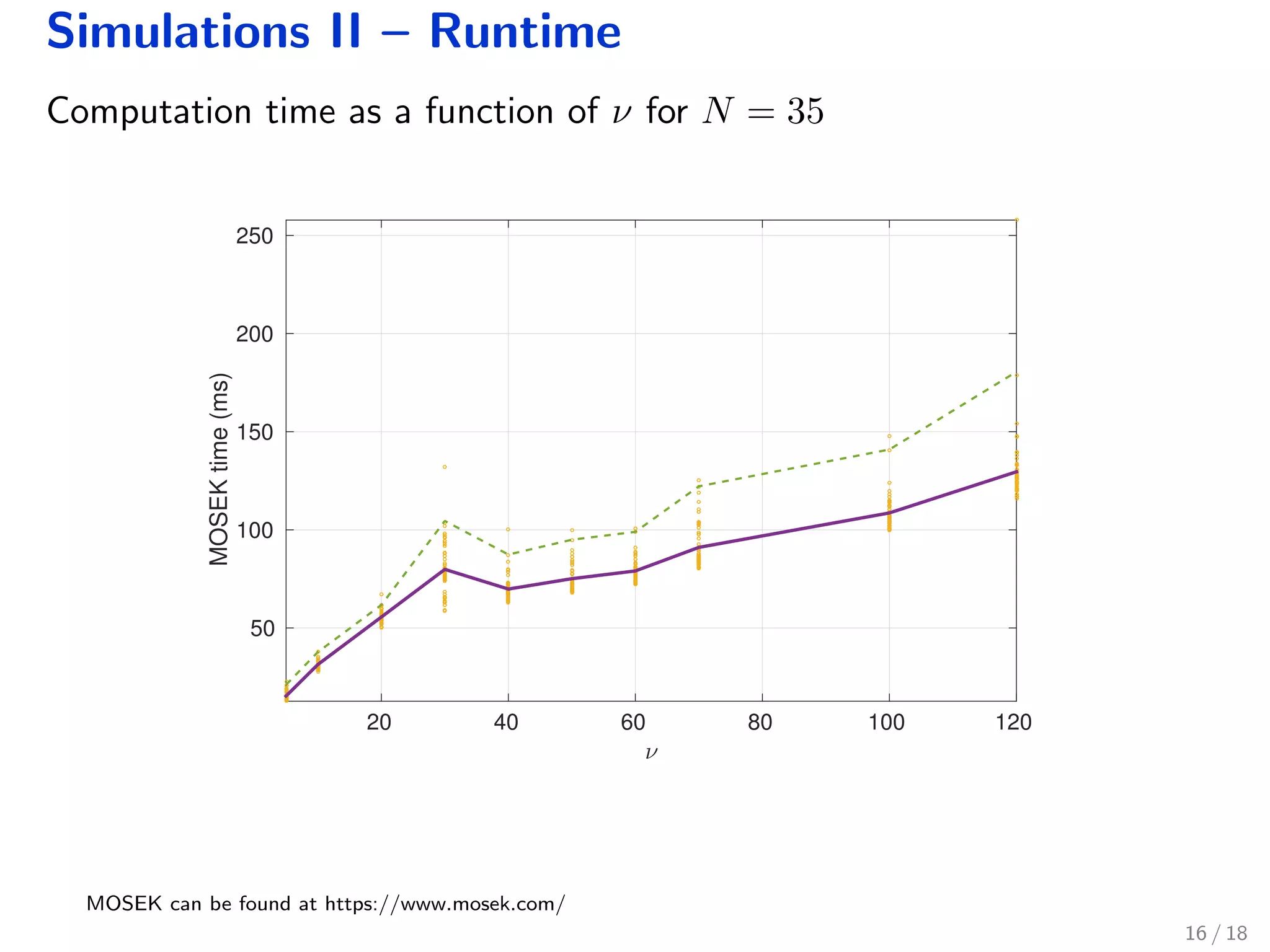
The document discusses robust model predictive control (MPC) for fractional-order discrete-time systems and introduces finite-dimensional approximations using fractional derivatives. It highlights the relevance of fractional systems in various applications, including pharmacokinetics and electromagnetic theory, and presents an MPC formulation that ensures constraints are met within a robustly positive invariant set. Simulations illustrate the approach's effectiveness, while also addressing ongoing questions regarding stability and application to controlled drug administration.

1. Robust MPC for fractional-order discrete-time systems
P. Sopasakisα,β, S. Ntouskasβ and H. Sarimveisβ
α Institute for Advanced Studies Lucca, Italy,
β National Technical University of Athens, Greece.
June 17, 2015

2. Fractional-order systems
and finite-dimensional approximations

3. Fractional derivatives
The Gr¨unwald-Letnikov derivative1 of order α > 0 is defined as
Dα
x(t) = lim
h→0+
∆α
hx(t)
hα
(1)
where ∆α
h is the fractional difference operator of order α with step size
h > 0 given by
∆α
hx(t) =
∞
j=0
(−1)j α
j
cα
j
x(t − kh), (2)
where
α
j
=
j−1
i=0
α − i
i + 1
. (3)
1
S. Samko, A. Kilbas, O. Marinhev, Fractional integral and derivatives, Gordon & Breach Science Publishers, 1993;
Section 20.
1 / 18

4. Fractional derivatives in action
A few examples:
Pharmacokinetics (Dokumetzidis et al. 2010, Magin et al. 2004)
Semi-infinite power transmission lines (Clarke et al., 2004)
Viscoelastic polymers (Hilfer 2000)
Anomalous diffusion (Magin 2010, Pereira 2010)
Electromagnetic theory (Sch¨afer and Kr¨uger 2006, Zelenyi and
Milovanov 2004)
Statistical mechanics (Tarasov 2005)
and many other...
2 / 18

5. Fractional systems
Fractional-order systems
l
i=1
AiDαi
x(t) = Bu(t) (4)
Euler-type discretisation [Replace Dαi h−αi ∆αi
h ]
l
i=1
¯Ai∆αi
h xk+1 = Buk (5)
Notice that ∆αi
h is an infinite-dimensional operator!
3 / 18

6. Finite-dimensional approximation
∆α
h can be written as
∆α
h = ∆α
h,ν + Rα
h,ν, (6)
where
∆α
h,νx(t) =
ν
j=0
cα
j x(t − kh), (7)
and Rα
h,ν is a bounded operator. If we plug (6) into the original system
we get
l
i=1
¯Ai∆αi
h,νxk+1
Finite dimensional
+
l
i=1
¯AiRαi
h,νxk+1
Bounded term
= Buk (8)
4 / 18

7. LTI approximation
We can now write the system as an LTI with a bounded disturbance
term dk as follows
˜xk+1 = A˜xk + Buk + Gdk, (9)
with state ˜xk = (xk, xk−1, . . . , xk−ν+1) and dk ∈ Dν ⊆ Rn. Assuming
xk ∈ X where X is a balanced compact set, we have
Dν =
l
i=1
− ˆA−1
0
¯AiΨν(αi)X, (10)
where Ψν(α) = ∞
j=0 |cα
j | and ˆA0 = l
i=1
¯Aicαi
j .
5 / 18

8. Ψν(α) is quickly decreasing with ν
ν
50 100 150 200 250 300
Ψν
(α)
10 -2
10 -1
10 0
α=0.7
α=0.5
α=0.4
...and as a result, Dν can become arbitrarily small for adequately large ν!
6 / 18

9. Model Predictive Control
using the approximate system model

10. Why MPC?
Because...
Optimisation-based control
Accounts for state/input constraints xk ∈ X, uk ∈ U.
7 / 18

11. Tube-based MPC
Nominal System
Tube-based MPC
+
-
+
+
Fractional System
v
u
Ke
K
e
˜x
˜z
Concept: The control action u is
calculated as
uk = vk + Kek,
where ek = ˜xk − ˜zk and vk is
computed by an MPC controller.
See: D.Q. Mayne, M.M. Seron, S.V. Rakovi´c, “Robust model predictive control of constrained linear systems with
bounded disturbances,” Automatica 41(2), 219–224, 2005.
8 / 18

12. Tube-based MPC
The set
S∞ =
∞
i=0
Ai
KGDν (11)
is robustly positive invariant for the deviation dynamics
ek+1 = AKek + Gdk (12)
Choosing ˜z0 = ˜x0 we have
˜xk ∈ {˜zk} ⊕ S∞, (13)
so the constraints will be satisfied if
˜zk ∈ X S∞, (14a)
˜vk ∈ U KS∞. (14b)
See: J. B. Rawlings and D. Q. Mayne, Model Predictive Control: Theory and Design. Nob Hill Publishing, 2009.
9 / 18

13. This leads to the following MPC formulation:
PN :VN (˜zk) = min
vk∈VN (˜zk)
VN (˜zk, vk), (15)
The terminal set ˜Xf and cost function Vf are selected according to the stabilising conditions in D. Mayne, J. Rawlings,
C. Rao, and P. Scokaert, “Constrained model predictive control: Stability and optimality,” Automatica 36 (6), 789–814, 2000.
10 / 18

14. This leads to the following MPC formulation:
PN :VN (˜zk) = min
vk∈VN (˜zk)
VN (˜zk, vk), (15)
where
VN (˜zk|k, vk)= Vf (˜zk+N|k)
Terminal cost
+
N−1
i=0
(˜zk+i|k, vk+i|k), (16)
The terminal set ˜Xf and cost function Vf are selected according to the stabilising conditions in D. Mayne, J. Rawlings,
C. Rao, and P. Scokaert, “Constrained model predictive control: Stability and optimality,” Automatica 36 (6), 789–814, 2000.
10 / 18

15. This leads to the following MPC formulation:
PN :VN (˜zk) = min
vk∈VN (˜zk)
VN (˜zk, vk), (15)
where
VN (˜zk|k, vk)= Vf (˜zk+N|k)
Terminal cost
+
N−1
i=0
(˜zk+i|k, vk+i|k), (16)
and for some S ⊇ S∞
VN (˜zk)=



v
˜zk+i+1|k=A˜zk+i|k+Bvk+i|k, ∀i∈N[0,N−1]
˜zk|k = ˜zk
˜zk+i|k ∈ ˜X S, ∀i∈N[1,N]
vk+i|k ∈ U KS, ∀i∈N[0,N−1]
˜zk+N|k ∈ ˜Xf Terminal constraints



(17)
The terminal set ˜Xf and cost function Vf are selected according to the stabilising conditions in D. Mayne, J. Rawlings,
C. Rao, and P. Scokaert, “Constrained model predictive control: Stability and optimality,” Automatica 36 (6), 789–814, 2000.
10 / 18

16. Closed-loop properties
The solution of PN is {v0(˜zk), v1(˜zk), . . . , vN−1(˜zk)} and the control law
is
κN (˜zk) = v0(˜zk), (18)
the input applied to the system is ρ(˜zk, ˜xk) = κN (˜zk) + K(˜xk − ˜zk) and
the closed-loop system (in terms of both ˜zk and ˜xk) becomes
˜xk+1 = A˜xk + Bρ(˜zk, ˜xk) + Gdk, (19a)
˜zk+1 = A˜zk + BκN (˜zk). (19b)
Stability: The set S∞ × {0} is exponentially stable for (19).
11 / 18

17. Simulation Results

18. Simulations I
Dynamical system:
D0.7
x(t) =


0 0 1
0 1 0
0 −1 1

 x(t) +


0 0
−1 0
1 1

 u(t), (20)
subject to the constraints
−


1
1
1

 ≤x(t) ≤


1
1
1

 (21a)
−
0.1
0.1
≤u(t) ≤
0.1
0.1
(21b)
and let ν = 20 and N = 35.
12 / 18

19. Simulations I
Closed-loop response...
2 4 6 8 10 12 14 16 18 20
−0.2
−0.1
0
0.1
0.2
State
xk
2 4 6 8 10 12 14 16 18 20
−0.04
−0.02
0
0.02
0.04
0.06
0.08
Control action
Time
uk
13 / 18

20. Simulations II
Dynamical system:
D0.7
x(t) =
1 0.9
−0.9 0.2
x(t) +
0
1
u(t), (22)
subject to the constraints
−
3
3
≤x(t) ≤
3
3
(23a)
−0.5 ≤u(t) ≤ 0.5 (23b)
The open-loop response of this system in unstable.
14 / 18

21. Simulations II
Closed-loop reponse...
time
0 5 10 15 20
x1
-0.5
0
0.5
1
1.5
2
ν=5
ν=10
ν=20
ν=50
time
0 5 10 15 20
x2
-3
-2
-1
0
ν=5
ν=10
ν=20
ν=50
15 / 18

22. Simulations II – Runtime
Computation time as a function of ν for N = 35
ν
20 40 60 80 100 120
MOSEKtime(ms)
50
100
150
200
250
MOSEK can be found at https://www.mosek.com/
16 / 18

23. Conclusions

24. Conclusions
Fractional-order discrete-time systems are infinite-dimensional,
We can approximate such systems as LTI with bounded additive
disturbance,
The order of approximation controls the magnitude of the
disturbance,
The approach is computationally tractable.
17 / 18

25. Ongoing
Under what conditions is the controlled system asymptotically stable?
Application: controlled drug administration (reference tracking).
18 / 18

26. Thank you for your attention
Acknowledgement: This work was funded by project 11ΣYN.10.1152, which is cofinanced by the European Union and Greece,
Operational Program “Competitiveness & Entrepreneurship”, NSFR 2007-2013 in the context of GSRT National action
“Cooperation”.

27. References
1. T. Clarke, B. N. Achar, and J. W. Hanneken, “MittagLeffler functions and transmission lines,” J. Molec. Liq.,
114(1–3), 159–163, 2004. Diffusion and Relaxation in Disordered Fractal Systems. Proceedings from the meeting on
Diffusion and Relaxation in Disordered Fractal Systems.
2. A. Dokoumetzidis, R. Magin, and P. Macheras, “Fractional kinetics in multi-compartmental systems,” J. Pharmacok.
Pharmacod., 37(5), 507–524, 2010.
3. R. Hilfer, Applications of Fractional Calculus in Physics. Singapore: World Scientific, 2000.
4. R. Magin, “Fractional calculus models of complex dynamics in bio- logical tissues,” Comp. & Math. with Appl.,
59(5), 1586–1593, 2010. Fractional Differentiation and Its Applications.
5. R. Magin, M. D. Ortigueira, I. Podlubny, and J. Trujillo, “On the fractional signals and systems,” Signal Processing,
91(3), 350–371, 2011. Advances in Fractional Signals and Systems.
6. L. Pereira, “Fractal pharmacokinetics,” Comput Math Methods Med., 11(2), 161–184, 2010.
7. S. Samko, A. Kilbas, O. Marinhev, Fractional integral and derivatives, Gordon & Breach Science Publishers, 1993.
8. L.M. Zelenyi, A.V. Milovanov, “Fractal topology and strange kinetics: from percolation theory to problems in cosmic
electrodynamics,” Physics Uspekhi 47 (2004) 749–788.
9. I. Sch¨afer and K. Kr¨uger, “Modelling of coils using fractional derivatives,” J. Magnetism & Magnetic Materials,
307(1), 91–98, 2006.

28. What are the stabilising conditions for MPC?
The following conditions are assumed for ˜Xf and Vf :
1. ˜Xf ⊆ ˜X = X × . . . × X, ˜Xf is closed and 0 ∈ ˜Xf ,
2. κN (˜z) ∈ U for all ˜z ∈ ˜Xf ,
3. A˜z + BκN (˜z) ∈ ˜Xf for all ˜z ∈ ˜Xf ,
4. Vf (˜z+) − Vf (˜z) ≤ (˜z, κN (˜z)), where ˜z+ = A˜z + BκN (˜z), for all
˜z ∈ ˜Xf .
These conditions can be found in D. Mayne, J. Rawlings, C. Rao, and P. Scokaert, “Constrained model predictive control:
Stability and optimality,” Automatica 36 (6), 789–814, 2000.

29. Is the controlled system asymptotically stable?
We have shown that the following condition entails asymptotic stability
properties for the controlled system:
j∈N
Aj
KG
i∈N[1,l]
− ˆA−1
0
¯AiΨν(αi)Bn
⊆ B¯n
,
for some > 0.