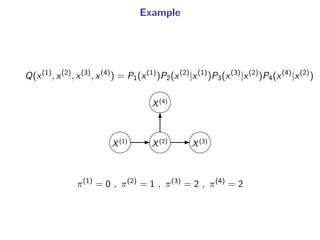
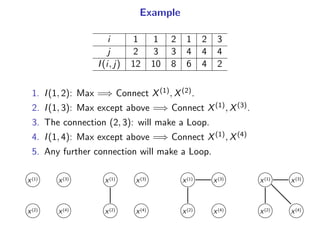
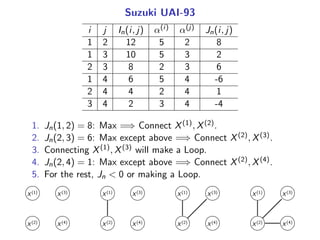
The document presents a generalization of the Chow-Liu algorithm for approximating distributions of general random variables and highlights its applications in artificial intelligence. It discusses the algorithm's methodology for constructing tree and forest structures minimizing Kullback-Leibler divergence by selecting edges based on mutual information. Additionally, the extension to general random variables is mathematically proven through examples involving Gaussian and finite-value random variables.

1. A Generalization of the Chow-Liu Algorithm and its
Applications to Artificial Intelligence
Joe Suzuki
Osaka University
July 14, 2010, ICAI 2010

2. Road Map
Statistical Learning Algorithms:
Chow-Liu for seeking Trees
Suzuki for seeking Forests
with Finite Random Valuables.
Our Contribution
Extend the Chow-Liu/Suzuki for General Random Variables
its Applications

3. Tree Distribution Approximation
Assumption
X := (X(1), · · · , X(N)) take Finite Values
P(x(1), · · · , x(N)): the Original Distribution
Q(x(1)
, · · · , x(N)
) :=
∏
π(j)=0
Pj (x(j)
)
∏
π(i)̸=0
Pi|π(i)(x(i)
|x(π(i))
)
π : {1, · · · , N} → {0, 1, · · · , N}
X(j) is the Parent of X(i) ⇐⇒ π(i) = j
X(i) is a Root ⇐⇒ π(i) = 0

4. Example
Q(x(1)
, x(2)
, x(3)
, x(4)
) = P1(x(1)
)P2(x(2)
|x(1)
)P3(x(3)
|x(2)
)P4(x(4)
|x(2)
)
X(1)
X(2)
X(3)
X(4)
E E
T
π(1)
= 0 , π(2)
= 1 , π(3)
= 2 , π(4)
= 2

5. Kullback-Leibler and Mutual Information
Kullback-Leibler Information
D(P||Q) :=
∑
x(1),··· ,x(N)
P(x(1)
, · · · , x(N)
) log
P(x(1), · · · , x(N))
Q(x(1), · · · , x(N))
(distribution difference)
Mutual Infomation
I(X, Y ) :=
∑
x,y
PXY (x, y) log
PXY (x, y)
PX (x)PY (y)
(correlation)

6. The Chow-Liu Algorithm
P: the Original
Q: its Tree Approximation
We wish to find Q s.t. D(P||Q) → Min
Find such Parents (π(1), · · · , π(N))
Chow-Liu, 1968
Continue to select an edge (X(i), X(j)) s.t. I(X(i), X(j)) → Max
unless adding it makes a Loop.

7. Example
i 1 1 2 1 2 3
j 2 3 3 4 4 4
I(i, j) 12 10 8 6 4 2
1. I(1, 2): Max =⇒ Connect X(1), X(2).
2. I(1, 3): Max except above =⇒ Connect X(1), X(3).
3. The connection (2, 3): will make a Loop.
4. I(1, 4): Max except above =⇒ Connect X(1), X(4)
5. Any further connection will make a Loop.

8. X(2)
X(4)
X(1)
X(3)

9. X(2)
X(4)
X(1)
X(3)

10. X(2)
X(4)
X(1)
X(3)

11. X(2)
X(4)
X(1)
X(3)
d
dd

12. Chow-Liu: the Procedure
V = {1, · · · , N}
I(i, j) := I(X(i), X(j)) (i ̸= j)
1. E := {};
2. E := {{i, j}|i ̸= j};
3. for {i, j} ∈ E maximizing Ii,j , E := E{{i, j}};
4. For (V , E ∪ {{i, j}}) not containing a loop: E := E ∪ {{i, j}};
5. If E ̸= {}, go to 3. and terminate otherwise;
Chow-Liu gives the Optimal (mathematically proved).
Q expressed by G = (V , E) minimizes D(P||Q).

13. The Chow-Liu Algorithm for Learning
Only n examples are given xn := {(x
(1)
i , · · · , x
(N)
i )}n
i=1
Use Empirical MI:
In(i, j) =
1
n
∑
x,y
ci,j (x, y) log
ci,j (x, y)
ci (x)cj (y)
ci,j (x, y), ci (x), cj (y): Frequencies in xn
Seeking only a Tree
Seeking a Forest as well as a Tree (Suzuki, UAI-93): use
Jn(i, j) := In(i, j) −
1
2
(α(i)
− 1)(α(j)
− 1) log n
Stop when Jn(i, j) 0.
α(i): How many values X(i) takes.

14. Suzuki UAI-93
i j In(i, j) α(i) α(j) Jn(i, j)
1 2 12 5 2 8
1 3 10 5 3 2
2 3 8 2 3 6
1 4 6 5 4 -6
2 4 4 2 4 1
3 4 2 3 4 -4
1. Jn(1, 2) = 8: Max =⇒ Connect X(1), X(2).
2. Jn(2, 3) = 6: Max except above =⇒ Connect X(2), X(3).
3. Connecting X(1), X(3) will make a Loop.
4. Jn(2, 4) = 1: Max except above =⇒ Connect X(2), X(4).
5. For the rest, Jn 0 or making a Loop.

15. X(2)
X(4)
X(1)
X(3)

16. X(2)
X(4)
X(1)
X(3)

17. X(2)
X(1)
X(4)
X(3)

18. X(2)
X(4)
X(1)
X(3)