The document discusses a proposed method for recursive compressed sensing, demonstrating that it is significantly faster than existing methods. It covers various optimization techniques including forward-backward splitting and Newton methods, and their applications in solving sparse coding problems. Additionally, simulations and the implications of this method in fields like MRI, radio-astronomy, and medical imaging are highlighted.

1. Recursive Compressed Sensing
Pantelis Sopasakis∗
Presentation at ICTEAM – UC Louvain, Belgium
joint work with N. Freris† and P. Patrinos‡
∗ IMT Institute for advanced studies Lucca, Italy
† NYU, Abu Dhabi, United Arab Emirates
‡ ESAT, KU Leuven, Belgium
April 7, 2016

2. Motivation
MRI
Radio-astronomy
Holography
Seismology
Photography
Radars
Facialrecognition
Speech
recognition
Fault detection
Medical
imaging
Facialrecognition
Particlephysics
Video processing
ECG
Encryption
Communication
networks
System identification
Compressed
Sensing
1 / 55

3. Spoiler alert!
The proposed method is an order of magnitude faster compared to
other reported methods for recursive compressed sensing.
2 / 55

4. Outline
1. Forward-Backward Splitting
2. The Forward-Backward envelope function
3. The Forward-Backward Newton method
4. Recursive compressed sensing
5. Simulations
3 / 55

5. I. Forward-Backward Splitting

6. Forward-Backward Splitting
Problem structure
minimize ϕ(x) = f(x) + g(x)
where
1. f, g : Rn → ¯R are proper, closed, convex
2. f has L-Lipschitz gradient
3. g is prox-friendly, i.e., its proximal operator
proxγg(v) := arg min
z
g(z) + 1
2 v − z 2
is easily computable[1]
.
[1]
Parikh & Boyd 2014; Combettes & Pesquette, 2010.
4 / 55

7. Example #1
Constrained QPs
minimize 1
2x Qx + q x
f
+ δ(x | B)
g
where B is a set on which projections are easy to compute and
δ(x | B) =
0, if x ∈ B,
+∞, otherwise
Then proxγg(x) = proj(x | B).
5 / 55

8. Example #2
LASSO problems
minimize 1
2 Ax − b 2
f
+ λ x 1
g
Indeed,
1. f is cont. diff/ble with f(x) = A (Ax − b)
2. g is prox-friendly
6 / 55

9. Other examples
Constrained optimal control
Elastic net
Sparse log-logistic regression
Matrix completion
Subspace identification
Support vector machines
7 / 55

10. Forward-Backward Splitting
FBS offers a generic framework for solving such problems using the
iteration
xk+1
= proxγg(xk
− γ f(xk
)) =: Tγ(xk),
for γ < 2/L.
Features:
1. ϕ(xk) − ϕ ∈ O(1/k)
2. with Nesterov’s extrapolation ϕ(xk) − ϕ ∈ O(1/k2)
8 / 55

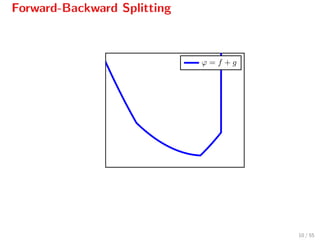
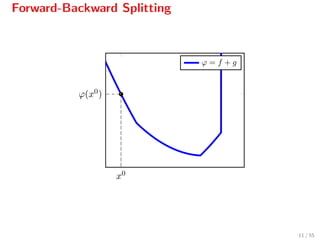
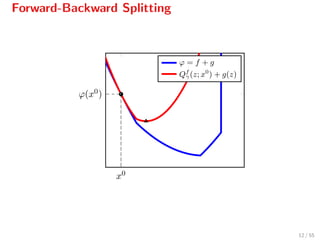
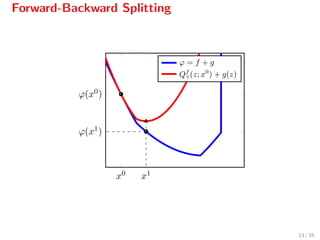
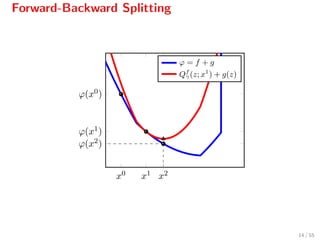
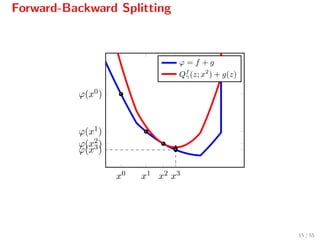
11. Forward-Backward Splitting
The iteration
xk+1
= proxγg(xk
− γ f(xk
)),
can be written as[2]
xk+1
= arg min
z
f(xk
) + f(xk
), z − xk
+ 1
2γ z − xk 2
Qf
γ(z,xk)
+g(z) ,
where Qf
γ(z, xk) serves as a quadratic model for f[3]
.
[2]
Beck and Teboulle, 2010.
[3]
Qf
γ (·, xk
) is the linearization of f at xk
plus a quadratic term; moreover, Qf
γ (z, xk
) ≥ f(x) and Qf
γ (z, z) = f(z).
9 / 55

12. Forward-Backward Splitting
x0
ϕ(x0)
ϕ = f + g
10 / 55

13. Forward-Backward Splitting
x0
ϕ(x0)
ϕ = f + g
11 / 55

14. Forward-Backward Splitting
x0
ϕ(x0)
ϕ = f + g
Qf
γ(z; x0
) + g(z)
12 / 55

15. Forward-Backward Splitting
x0 x1
ϕ(x0)
ϕ(x1)
ϕ = f + g
Qf
γ(z; x0
) + g(z)
13 / 55

16. Forward-Backward Splitting
x0 x1 x2
ϕ(x0)
ϕ(x1)
ϕ(x2)
ϕ = f + g
Qf
γ(z; x1
) + g(z)
14 / 55

17. Forward-Backward Splitting
x0 x1 x2 x3
ϕ(x0)
ϕ(x1)
ϕ(x2)
ϕ(x3)
ϕ = f + g
Qf
γ(z; x2
) + g(z)
15 / 55

18. Overview
Generic convex optimization problem
minimize f(x) + g(x).
The generic iteration
xk+1
= proxγg(xk
− γ f(xk
))
is a fixed-point iteration for the optimality condition
x = proxγg(x − γ f(x ))
16 / 55

19. Overview
It generalizes several other methods
xk+1
=



xk − γ f(xk) gradient method, g = 0
ΠC(xk − γ f(xk)) gradient projection, g = δ(· | C)
proxγg(xk) proximal point algorithm, f = 0
There are several flavors of proximal gradient algorithms[4]
.
[4]
Nesterov’s accelerated method, FISTA (Beck & Teboulle), etc.
17 / 55

20. Shortcomings
FBS are first-order methods, therefore, they can be slow!
Overhaul. Use a better quadratic model for f[5]
:
Qf
γ,B(z, xk
) = f(xk
) + f(xk
), z − xk
+ 1
2γ z − xk 2
Bk ,
where Bk is (an approximation of) 2f(x).
Drawback. No closed form solution of the inner problem.
[5]
As in Becker & Fadili 2012; Lee et al. 2012; Tran-Dinh et al. 2013.
18 / 55

21. II. Forward-Backward Envelope

22. Forward-Backward Envelope
The Forward-Backward envelope of ϕ is defined as
ϕγ(x) = min
z
f(x) + f(x), z − x + g(z) + 1
2γ z − x 2
,
with γ ≤ 1/L. Let’s see how it looks...
19 / 55

23. Forward-Backward Envelope
x
ϕ(x)
ϕγ(x)
ϕ
20 / 55

24. Forward-Backward Envelope
x
ϕ(x)
ϕγ(x)
ϕ
21 / 55

25. Forward-Backward Envelope
x
ϕ(x)
ϕγ(x)
ϕ
ϕγ
22 / 55

26. Properties of FBE
Define
Tγ(x) = proxγg(x − γ f(x))
Rγ(x) = γ−1
(x − Tγ(x))
FBE upper bound
ϕγ(x) ≤ ϕ(x) − 1
2γ Rγ(x) 2
FBE lower bound
ϕγ(x) ≥ ϕ(Tγ(x)) +
1−γLf
2γ Rγ(x) 2
x Tγ(x)
ϕ(x)
ϕ(Tγ(x))
ϕγ(x)
ϕ
ϕγ
x = Tγ(x )
ϕ(x )
ϕ
ϕγ
23 / 55

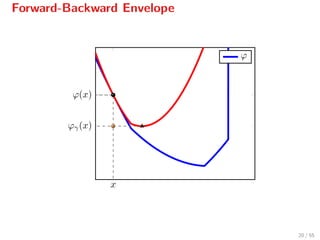
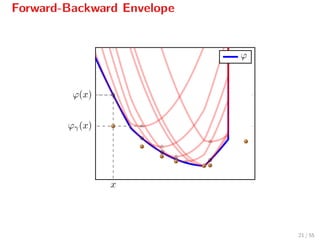
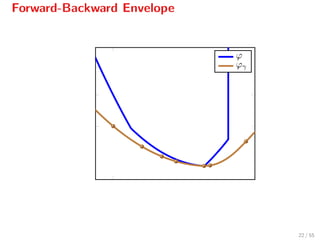
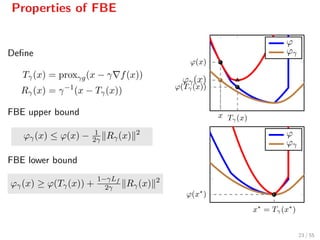
27. Properties of FBE
Ergo: Minimizing ϕ is equivalent to minimizing its FBE ϕγ.
inf ϕ = inf ϕγ
arg min ϕ = arg min ϕγ
However, ϕγ is continuously diff/able[6]
whenever f ∈ C2.
[6]
More about the FBE: P. Patrinos, L. Stella and A. Bemporad, 2014.
24 / 55

28. FBE is C2
FBE can be written as
ϕγ(x) = f(x) − γ
2 f(x) 2
+ gγ
(x − f(x)),
where gγ is the Moreau envelope of g,
gγ
(v) = min
z
{g(z) + 1
2γ z − v 2
}
gγ is a smooth approximation of g with gγ(x) = γ−1(x − proxγg(x)). If
f ∈ C2, then
ϕγ(x) = (I − γ 2
f(x))Rγ(x).
Therefore,
arg min ϕ = arg min ϕγ = zer ϕγ.
25 / 55

29. The Moreau envelope
g(x) = |x|
g0.1
g10
26 / 55

30. Forward-Backward Newton
Since ϕγ is C1 but not C2, we may not apply a Newton method.
The FB Newton method is a semi-smooth method for minimizing ϕγ
using a notion of generalized differentiability.
The FBN iterations are
xk+1
= xk
+ τkdk
,
where dk is a Newton direction given by
Hkdk
= − ϕγ(xk
),
Hk ∈ ∂2
Bϕγ(xk
),
∂B is the so-called B-subdifferential (we’ll define it later)
27 / 55

31. III. Forward-Backward Newton

32. Optimality conditions
LASSO problem
minimize 1
2 Ax − b 2
f
+ λ x 1
g
.
Optimality conditions
− f(x ) ∈ ∂g(x ).
where f(x) = A (Ax − b) and ∂g(x)i = λ sign(xi) for xi = 0 and
∂g(x)i = [−λ, λ] otherwise, so
− if(x ) = λ sign(xi ), if xi = 0,
| if(x )| ≤ λ, otherwise
28 / 55

33. Optimality conditions
If we knew the set
α = {i : xi = 0},
β = {j : xj = 0},
we would be able to write down the optimality conditions as
Aα Aαxα = Aα b + λ sign(xα)
Goal. Devise a method to determine α efficiently.
29 / 55

34. Optimality conditions
We may write the optimality conditions as follows
x = proxγg(x − γ f(x )),
where
proxγg(z)i = sign(zi)(|zi| − γλ)+.
ISTA and FISTA are method for the iterative solution of these
conditions. Instead, we are looking for a zero of the fixed-point residual
operator
Rγ(x) = x − proxγg(x − γ f(x)).
30 / 55

35. B-subdifferential
For a function F : Rn → Rn which is almost everywhere differentiable, we
define its B-subdifferential to be[7]
∂BF(x) := B ∈ Rn×n ∃{xn}n : xn → x,
Rγ(xn) exists and Rγ(xn) → B
.
[7]
See Facchinei & Pang, 2004
31 / 55

36. Forward-Backward Newton
Rγ(x) is nonexpansive ⇒ Lipschitz ⇒ Differentiable a.e. ⇒ B-sub-
differentiable (∂BRγ(x)). The proposed algorithm takes the form
xk+1
= xk
− τkH−1
k Rγ(xk
), with Hk ∈ ∂BRγ(xk
).
When close to the solution, all Hk are nonsingular. Take
Hk = I − Pk(I − γA A),
where Pk is diagonal with (Pk)ii = 1 iff i ∈ αk, where
αk = {i : |xk
i − γ if(xk
i )| > γλ}
The scalar τk is computed by a simple line search method to ensure
global convergence of the algorithm.
32 / 55

37. Forward-Backward Newton
The Forward-Backward Newton method can be concisely written as
xk+1
= xk
+ τkdk
.
The Newton direction dk is determined as follows without the need to
formulate Hk
dk
βk
= −(Rγ(xk
))βk
,
γAαk
Aαk
dk
αk
= −(Rγ(xk
))αk
− γAαk
Aβk
dk
βk
.
For the method to converge globally, we compute τk so that the Armijo
condition is satisfied for ϕγ
ϕγ(xk
+ τkdk
) ≤ ϕγ(xk
) + ζτk ϕγ(xk
) dk
.
33 / 55

38. Forward-Backward Newton
Require: A, y, λ, x0,
γ ← 0.95/ A 2
x ← x0
while Rγ(x) > do
α ← {i : |xi − γ if(x)| > γλ}
β ← {i : |xi − γ if(x)| ≤ γλ}
dβ ← −xβ
sα ← sign(xα − γ αf(x))
Solve Aα Aα(xα + dα) = Aα y − λsα
τ ← 1
while ϕγ(x + τd) ≤ ϕγ(x) + ζτ ϕγ(x) d do
τ ← 1
2τ
end while
x ← x + τd
end while
34 / 55

39. Speeding up FBN by Continuation
1. In applications of LASSO we have x 0 ≤ m n[8]
[8]
The zero-norm of x, x 0, is the number of its nonzeroes.
35 / 55

40. Speeding up FBN by Continuation
1. In applications of LASSO we have x 0 ≤ m n[8]
2. If λ ≥ λ0 := f(x0) ∞, then supp(x) = ∅
[8]
The zero-norm of x, x 0, is the number of its nonzeroes.
35 / 55

41. Speeding up FBN by Continuation
1. In applications of LASSO we have x 0 ≤ m n[8]
2. If λ ≥ λ0 := f(x0) ∞, then supp(x) = ∅
3. We relax the optimization problem solving
P(¯λ) : minimize 1
2 Ax − y 2
+ ¯λ x 1
[8]
The zero-norm of x, x 0, is the number of its nonzeroes.
35 / 55

42. Speeding up FBN by Continuation
1. In applications of LASSO we have x 0 ≤ m n[8]
2. If λ ≥ λ0 := f(x0) ∞, then supp(x) = ∅
3. We relax the optimization problem solving
P(¯λ) : minimize 1
2 Ax − y 2
+ ¯λ x 1
4. Once we have approximately solved P(¯λ) we update ¯λ as
¯λ ← max{η¯λ, λ},
until eventually ¯λ = λ.
[8]
The zero-norm of x, x 0, is the number of its nonzeroes.
35 / 55

43. Speeding up FBN by Continuation
1. In applications of LASSO we have x 0 ≤ m n[8]
2. If λ ≥ λ0 := f(x0) ∞, then supp(x) = ∅
3. We relax the optimization problem solving
P(¯λ) : minimize 1
2 Ax − y 2
+ ¯λ x 1
4. Once we have approximately solved P(¯λ) we update ¯λ as
¯λ ← max{η¯λ, λ},
until eventually ¯λ = λ.
5. This way we enforce that (i) |αk| increases smoothly, (ii) |αk| < m,
(iii) Aαk
Aαk
remains always positive definite.
[8]
The zero-norm of x, x 0, is the number of its nonzeroes.
35 / 55

44. Speeding up FBN by Continuation
Require: A, y, λ, x0, η ∈ (0, 1),
¯λ ← max{λ, f(x0) ∞}, ¯ ←
while ¯λ > λ or Rγ(xk; ¯λ) > do
xk+1 ← xk + τkdk (dk: Newton direction, τk line search)
if Rγ(xk; ¯λ) ≤ λ¯ then
¯λ ← max{λ, η¯λ}
¯ ← η¯
end if
end while
36 / 55

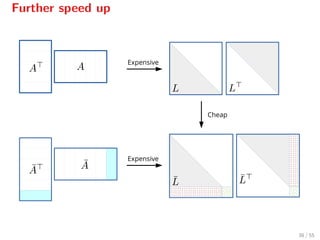
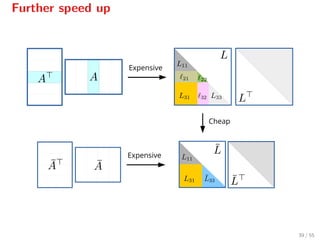
45. Further speed up
When Aα is positive definite[9]
, we may compute a Cholesky factorization
of Aα0
Aα0 and then update the Cholesky factorization of Aαk+1
Aαk+1
using the factorization of Aαk
Aαk
.
[9]
In practice, always (when the continuation heuristic is used). Furthermore, α0 = ∅.
37 / 55

46. Further speed up
Cheap
Expensive
Expensive
38 / 55

47. Further speed up
Cheap
Expensive
Expensive
39 / 55

48. Overview
Why FBN?
Fast convergence
Very fast convergence when close to the solution
Few, inexpensive iterations
The FBE serves as a merit function ensuring global convergence
40 / 55

49. IV. Recursive Compressed Sensing

50. Introduction
We say that a vector x ∈ Rn is s-sparse if it has at most s nonzeroes.
Assume that a sparsely-sampled signal y ∈ Rm (m n) is produced by
y = Ax,
by an s-sparse vector x and a sampling matrix A. In reality, however,
measurements will be noisy
y = Ax + w.
41 / 55

51. Sparse Sampling
42 / 55

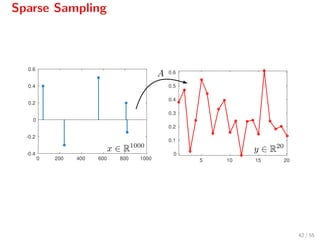
52. Sparse Sampling
We require that A satisfies the restricted isometry property[10]
, that is
(1 − δs) x 2
≤ Ax 2
≤ (1 + δs) x 2
A typical choice is a random matrix A with entries drawn from N(0, 1
m )
with m = 4s.
[10]
This can be established using the Johnson-Lindenstrauss lemma.
43 / 55

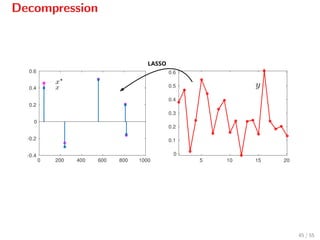
53. Decompression
Assuming that
w ∼ N(0, σ2I),
the smallest element of |x| is not too small (> 8σ
√
2 ln n),
λ = 4σ
√
2 ln n,
the LASSO recovers the support of x[11]
, that is
x = arg min 1
2 Ax − y 2
+ λ x 1,
has the same support as the actual x.
[11]
Cand`es & Plan, 2009.
44 / 55

54. Decompression
LASSO
45 / 55

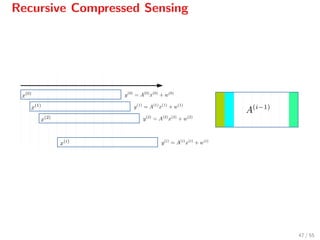
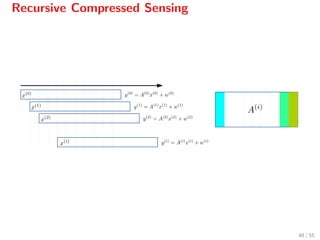
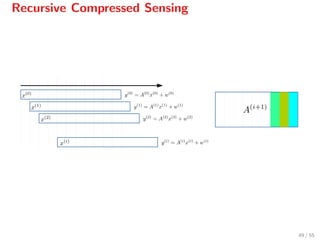
55. Recursive Compressed Sensing
Define
x(i)
:= xi xi+1 · · · xi+n−1
Then x(i) produces the measured signal
y(i)
= A(i)
x(i)
+ w(i)
.
Sampling is performed with a constant matrix A[12]
and
A(0)
= A,
A(i+1)
= A(i)
P,
where P is a permutation matrix which shifts the columns of A leftwards.
[12]
For details see: N. Freris, O. ¨O¸cal and M. Vetterli, 2014.
46 / 55

56. Recursive Compressed Sensing
47 / 55

57. Recursive Compressed Sensing
48 / 55

58. Recursive Compressed Sensing
49 / 55

59. Recursive Compressed Sensing
Require: Stream of observations, Window size n, Sparsity s
λ ← 4σ
√
2 ln n and m ← 4s
Construct A ∈ Rm×n with entries from N(0, 1
m )
A(0) ← A, x
(0)
◦ ← 0
for i = 0, 1, . . . do
1. Sample y(i) ∈ Rm
2. Support estimation (using the initial guess x
(i)
◦ )
x
(i)
= arg min 1
2 A(i)
x(i)
− y(i) 2
+ λ x(i)
1
3. Perform debiasing
4. x
(i+1)
◦ ← P x
(i)
5. A(i+1) ← A(i)P
end for
50 / 55

60. V. Simulations

61. Simulations
We compared the proposed methodology with
ISTA (or proximal gradient method)
FISTA (or accelerated ISTA)
ADMM
L1LS (interior point method)
51 / 55

62. Simulations
For a 10%-sparse stream
Window size ×10 4
0.5 1 1.5 2
Averageruntime[s]
10 -1
10 0
10 1
FBN
FISTA
ADMM
L1LS
52 / 55

63. Simulations
For n = 5000 varying the stream sparsity
Sparsity [%]
0 5 10 15
Averageruntime[s]
10 -1
10 0
FBN
FISTA
ADMM
L1LS
53 / 55

64. References
1. S.-J. Kim, K. Koh, M. Lustig, S. Boyd, and D. Gorinevsky, “An interior- point
method for large-scale 1 -regularized least squares,” IEEE J Select Top Sign Proc,
1(4), pp. 606–617, 2007.
2. A. Beck and M. Teboulle, “A fast iterative shrinkage-thresholding algo- rithm for
linear inverse problems,” SIAM J Imag Sci, 2(1), pp. 183–202, 2009.
3. S. Becker and M. J. Fadili, “A quasi-Newton proximal splitting method,” in
Advances in Neural Information Processing Systems, vol. 1, pp. 2618–2626, 2012.
4. A. Beck and M. Teboulle, “A fast iterative shrinkage-thresholding algorithm for
linear inverse problems,” SIAM J Imag Sci, 2(1), pp. 183–202, 2009.
5. P. Patrinos, L. Stella and A. Bemporad, “Forward-backward truncated Newton
methods for convex composite optimization,” arXiv:1402.6655, 2014.
6. P. Sopasakis, N. Freris and P. Patrinos, “Accelerated reconstruction of a
compressively sampled data stream,” 24th European Signal Processing
conference, submitted, 2016.
7. N. Freris, O. ¨O¸cal and M. Vetterli, “Recursive Compressed Sensing,”
arXiv:1312.4895, 2013.
54 / 55

65. Thank you for your attention.
55 / 55