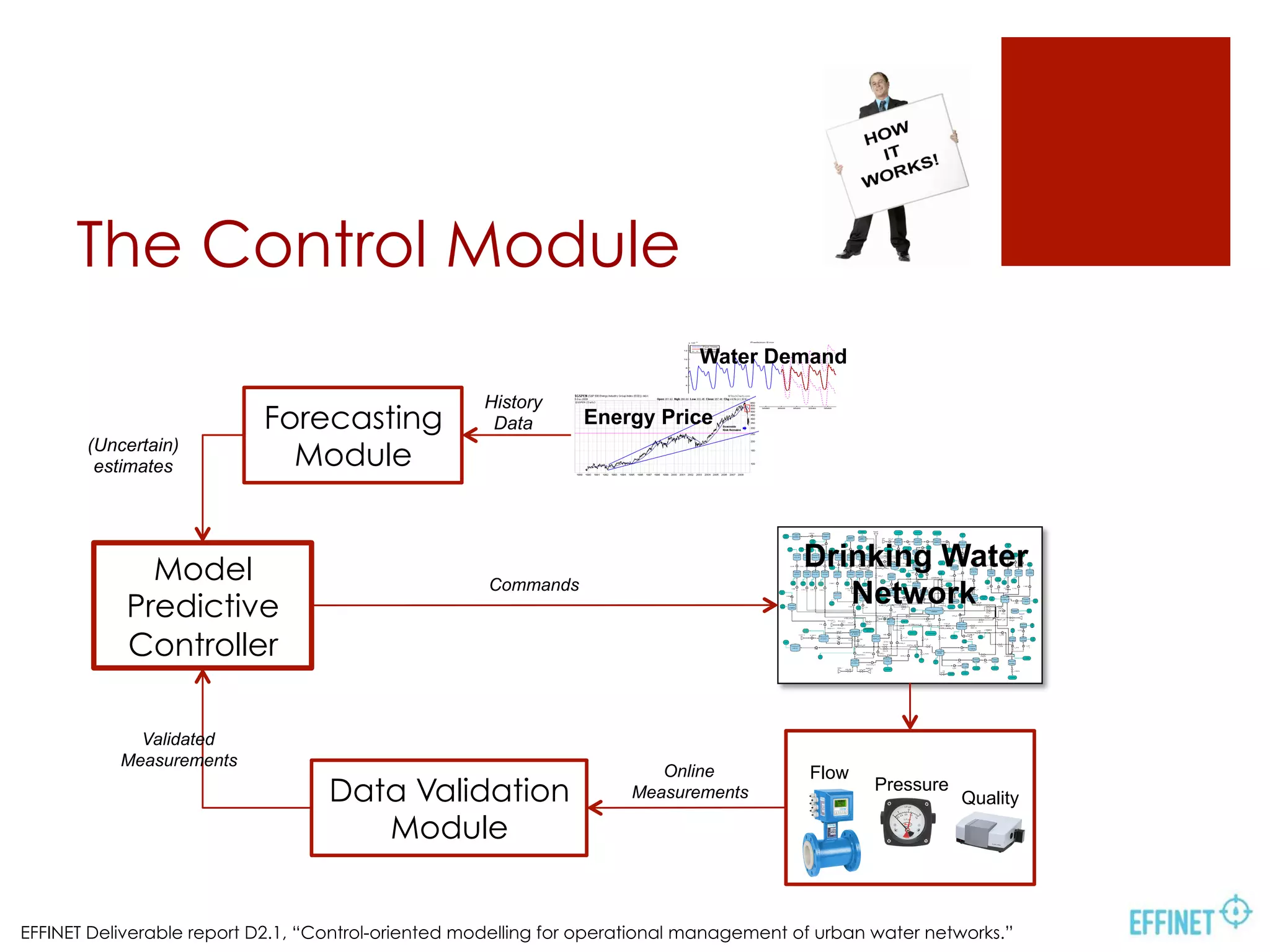
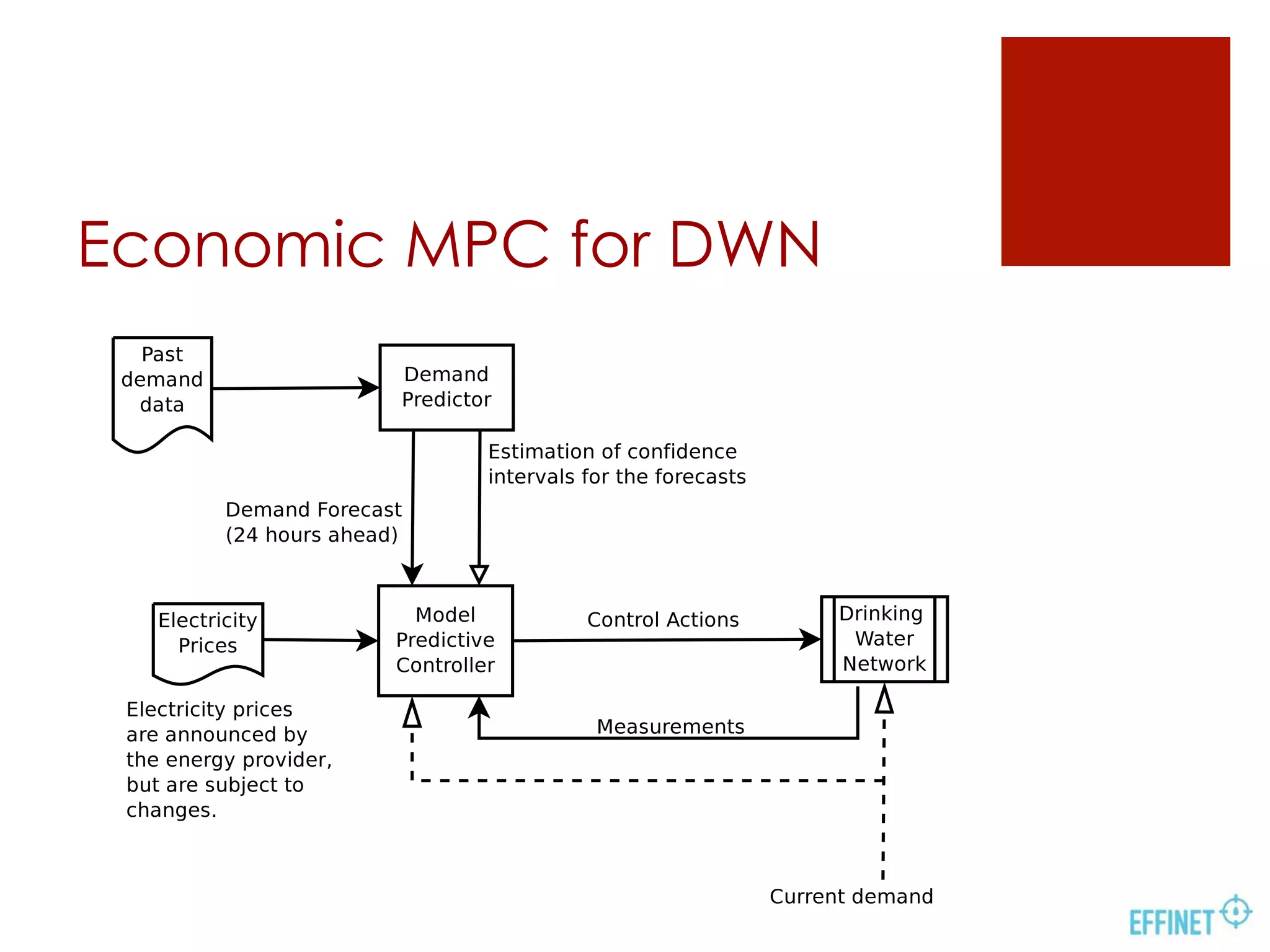
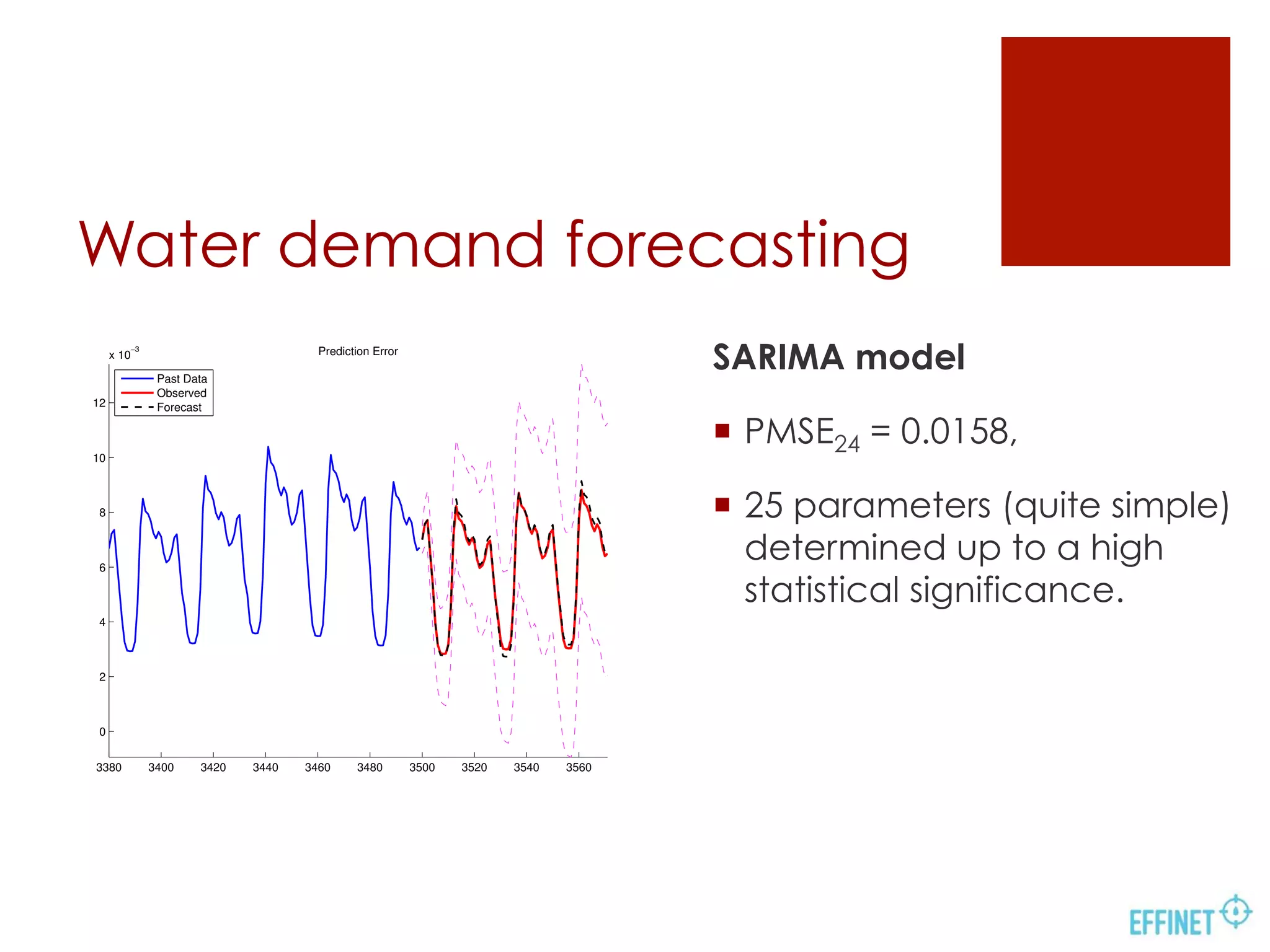
This document summarizes research on using model predictive control (MPC) for optimizing the operation of large-scale drinking water networks. Key points: - MPC aims to reduce energy costs while meeting demand and respecting constraints, using forecasts of water demand and energy prices. - Demand is forecasted using SARIMA, BATS and RBF-SVM models, with RBF-SVM achieving the best accuracy. - A hydraulic model is developed to predict network state based on inputs, disturbances, and constraints. 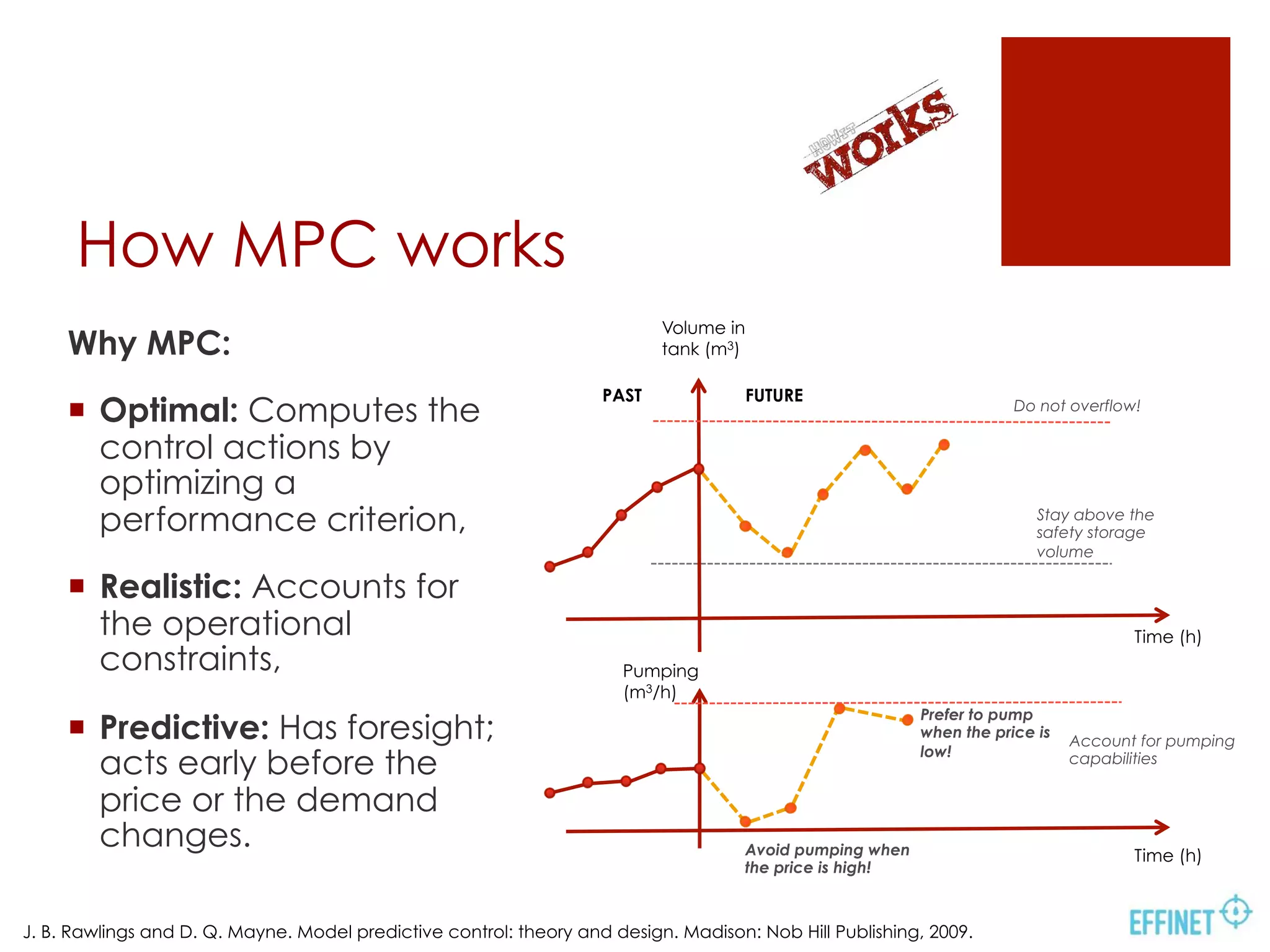- MPC optimizes pumping over a horizon while respecting constraints, using demand forecasts to anticipate future needs. - Simulation results on a real network show MPC achieving low costs while

1. Water demand
forecasting for the optimal
operation of large-scale
drinking water networks
the Barcelona case study
A.K. Sampathirao*, J.M. Grosso**, P. Sopasakis*, C.
Ocampo-Martinez**, A. Bemporad* and V. Puig**
* IMT Institute for Advanced Studies Lucca, Lucca, Italy,
** Automatic Control Dept., Technical University of Catalonia
(UPC), Barcelona, Spain.

2. DWN Control: Goals
¡ Reduce energy consumption for pumping,
¡ Meet the demand requirements,
¡ Deliver smooth control actions,
¡ Keep the storage above safety limits,
¡ Respect the technical limitations: pressure limits,
overflow limits & pumping capabilities,
¡ Have foresight: predict how the water demand
and energy cost will move and act accordingly.

3. Outline
¡ Description of the overall control system,
¡ Hydraulic model of the DWN,
¡ Modelling of the uncertain water demand time
series,
¡ Economic MPC: the control algorithm,
¡ Simulation results.

4. 3380 3400 3420 3440 3460 3480 3500 3520 3540 3560
0
2
4
6
8
10
12
x 10
−3 Prediction Error
Past Data
Observed
Forecast
The Control Module
Energy Price
Water Demand
Drinking Water
Network
Online
Measurements
Flow
Pressure
Quality
Forecasting
Module
History
Data
Data Validation
Module
Validated
Measurements
Commands
Model
Predictive
Controller
(Uncertain)
estimates
EFFINET Deliverable report D2.1, “Control-oriented modelling for operational management of urban water networks.”

5. Hydraulic model
xk+1 = Adxk + Bduk + Gddk,
0 = Euk + Eddk
¡ Based on mass balance equations,
¡ Linear time-invariant discrete time system,
¡ with input-disturbance couplings
State:
Storage in tanks
Input:
Pumping
Disturbance:
Water demand
Constraints mandated by
mass balance equations.
C. Ocampo-Martinez, V. Puig, G. Cembrano, R. Creus, and M. Minoves. Improving water management efficiency by using
optimization-based control strategies: the barcelona case study. Water Sci. & Tech.: Water supply, 9(5):565–575, 2009.

6. Water demand forecasting
¡ Three approaches bore fruit: SARIMA, BATS and
RBF-SVM,
¡ The predictive ability of the models was
evaluated using the average PMSE-24, that is:
PMSEHp
=
1
THp
k0+TX
k=k0
Hp
X
i=1
( ˆdk+i|k dk+i)2

7. Water demand forecasting
3380 3400 3420 3440 3460 3480 3500 3520 3540 3560
0
2
4
6
8
10
12
x 10
−3 Prediction Error
Past Data
Observed
Forecast
SARIMA model
¡ PMSE24 = 0.0158,
¡ 25 parameters (quite simple)
determined up to a high
statistical significance.

8. Water demand forecasting
RBF-SVM model
¡ PMSE24 = 0.0065,
¡ 229 parameters (complex),
¡ 10-fold cross-validation
gave q2 = 0.9952,
¡ Explanatory variables:
200 past demands plus a
set of binary calendar
variables,
¡ Stringent confidence
intervals.
3250 3260 3270 3280 3290 3300 3310 3320
3
4
5
6
7
8
9
10
x 10
−3
Time [hr]
Demand[m
3
hr
−1
]
RBF−SVM Prediction

9. 0 20 40 60 80 100 120 140 160 180 200
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
Time [h]
WaterDemandFlow[m3
/h]
Forecasting of Water Demand
FuturePast
Water demand forecasting
BATS model
¡ Box-Cox transformation,
ARMA errors, Trends and
Seasonality,
¡ PMSE24 = 0.0043,
¡ with just 26 parameters,
¡ Very stringent confidence
intervals.

10. Prefer to pump
when the price is
low!
Stay above the
safety storage
volume
PAST FUTURE
Volume in
tank (m3)
Time (h)
Do not overflow!
Time (h)
Pumping
(m3/h)
Avoid pumping when
the price is high!
Account for pumping
capabilities
Why MPC:
¡ Optimal: Computes the
control actions by
optimizing a
performance criterion,
¡ Realistic: Accounts for
the operational
constraints,
¡ Predictive: Has foresight;
acts early before the
price or the demand
changes.
How MPC works
J. B. Rawlings and D. Q. Mayne. Model predictive control: theory and design. Madison: Nob Hill Publishing, 2009.

11. Economic MPC for DWN
From the forecasting module: dk+j|k = ˆdk+j|k + ✏k+j|k
Estimation error, essentially bounded in:
Ek+j|k = {✏ : ✏min
k+j|k  ✏  ✏max
k+j|k}
xk+j|k = ˆxk+j|k +
jX
l=1
Al 1
Gd✏k+l|kThe state sequence will satisfy:
Nominal state sequence satisfying the
dynamics:
ˆxk+j+1|k = Ad ˆxk+j|k + Bduk+j|k + Gd
ˆdk+j|k

12. Economic MPC for DWN

13. Economic MPC for DWN
4500 4505 4510 4515 4520 4525 4530 4535 4540 4545
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
x 10
4
Time [hr]
Volume[m3
]
Safety Volume
Minimum Volume
Maximum Volume
MPC Upper Bound
MPC Lower Bound
Predicted Trajectory
Closed−loop trajectory
ˆxk+j|k 2 X
iM
j=1
Aj 1
GdEk+j|k
Bounds on the predicted state
sequence calculated by:
The sparsity of Gd enables this
computation!

14. Economic MPC for DWN
4500 4505 4510 4515 4520 4525 4530 4535 4540 4545
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
x 10
4
Time [hr]
Volume[m3
]
Safety Volume
Minimum Volume
Maximum Volume
MPC Upper Bound
MPC Lower Bound
Predicted Trajectory
Closed−loop trajectory
ˆxk+j+1|k = Ad ˆxk+j|k + Bduk+j|k+
+ Gd
ˆdk+j|k
Predicted state sequence
according to:

15. MPC: Performance
10 20 30 40 50 60 70 80 90
0.2
0.4
0.6
0.8
MPC Control Action (1~20)
ControlAction
10 20 30 40 50 60 70 80 90
0.2
0.4
0.6
0.8
MPC Control Action (21~46)
ControlAction
10 20 30 40 50 60 70 80 90
0
0.1
0.2
Time [hr]
WaterCost[e.u.]
MPC in action
• 88 demand nodes
• 63 tanks
• 114 pumping stations
• 17 flow nodes
50 100 150 200 250 300 350 400 450 500
4
5
6
7
8
Economic Cost (E.U.)
50 100 150 200 250 300 350 400 450 500
0.5
1
1.5
2
Smooth Operation Cost
0 50 100 150 200 250 300 350 400 450 500
0
2
4
6
Safety Storage Cost (× 107
)
Low price à Pumping
The system operator has
information about the
current and the
predicted operation cost.

16. 5 10 15 20 25 30 35 40 45 50 55
0
20
40
60
80
100
Closed−loop MPC Simulation
Time [hr]
Repletion[%]
5 10 15 20 25 30 35 40 45 50 55
0
0.5
1
1.5
Time [hr]
Demand[m
3
/s]
MPC: Performance
10 20 30 40 50 60 70 80 90
0.2
0.4
0.6
0.8
MPC Control Action (1~20)
ControlAction
10 20 30 40 50 60 70 80 90
0.2
0.4
0.6
0.8
MPC Control Action (21~46)
ControlAction
10 20 30 40 50 60 70 80 90
0
0.1
0.2
Time [hr]
WaterCost[e.u.]
Foresight: Tanks starts
loading up before a
DMA asks for water.

17. Work in progress
¡ Formulation of the control problem as a
stochastic economic MPC problem,
¡ Algorithms for the solution of large-scale
optimisation problems,
¡ GPGPU implementations for the efficient solution
of such optimisation algorithms.

18. Thank you for your attention.
This work was financially supported by the EU FP7 research project
EFFINET “Efficient Integrated Real-time monitoring and Control of
Drinking Water Networks,” grant agreement no. 318556.