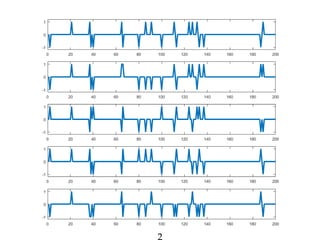
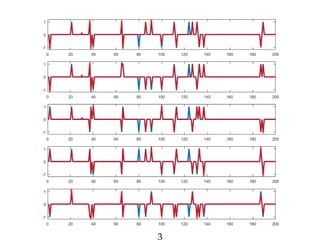
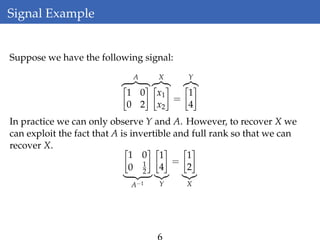
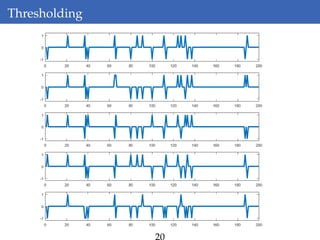
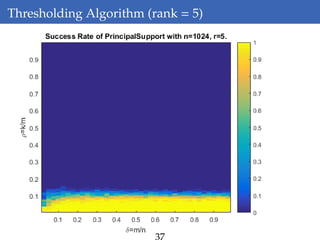
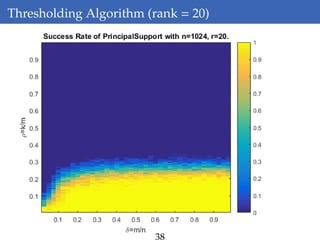
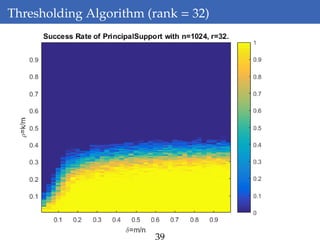
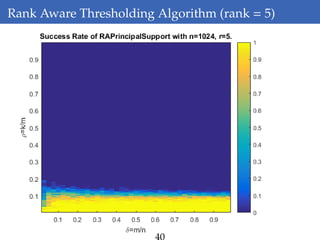
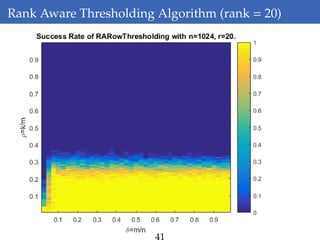
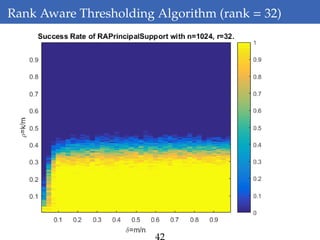
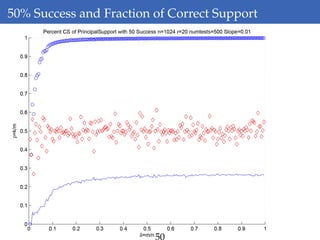
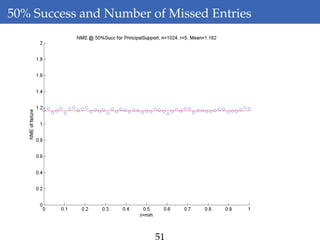
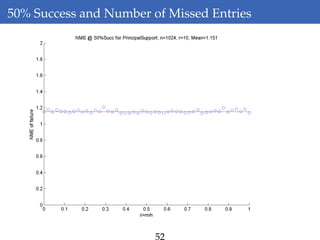
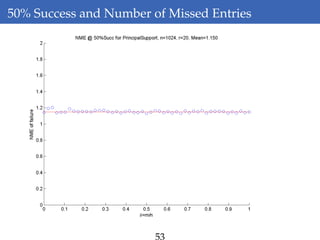
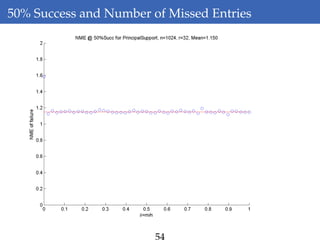
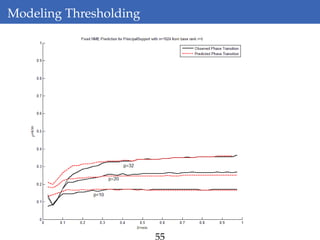
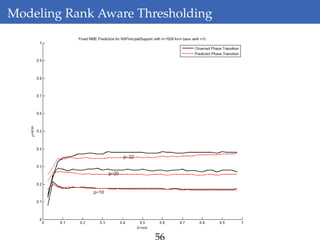
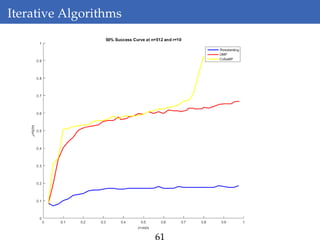
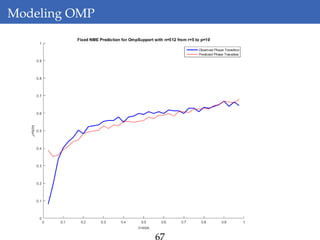
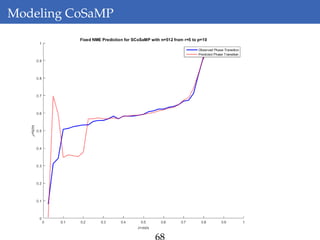
This document discusses rank-aware thresholding algorithms for compressed sensing. It begins by introducing compressed sensing and explaining how traditional linear algebra techniques cannot be used to recover sparse signals from undersampled measurements. It then describes how thresholding and rank-aware thresholding algorithms work by exploiting the sparsity of signals. The key points are that rank-aware thresholding outperforms standard thresholding by eliminating the "square-root bottleneck" and requires only O(k) measurements, versus O(k^2) for thresholding. Simulation results demonstrate this improvement. The document concludes by discussing modeling techniques to predict algorithm performance on very large problems that are impractical to simulate directly.

1. Rank-Awareness in Compressed Sensing
Caleb Leedy and Yimin Wu
MAP: Rank Aware Hard Thresholding for Sparse Approximation
Dr. Blanchard
February 9, 2016
1

2. 2

3. 3

4. What is Compressed Sensing?
Trying to recover a signal with minimal measurement.
We use matrices to represent this signal processing problem.
Original Signal : X
Measurement Matrix: A
Observation Matrix: Y
AX = Y
4

5. Signal Example
Suppose we have the following signal:
A
1 0
0 2
X
x1
x2
=
Y
1
4
In practice we can only observe Y and A. However, to recover X we
can exploit the fact that A is invertible and full rank so that we can
recover X.
5

6. Signal Example
Suppose we have the following signal:
A
1 0
0 2
X
x1
x2
=
Y
1
4
In practice we can only observe Y and A. However, to recover X we
can exploit the fact that A is invertible and full rank so that we can
recover X.
1 0
0 1
2
A−1
1
4
Y
=
1
2
X
6

7. Understanding the Matrices
Dimensions of Matrices:
X ∈ Rn×
A ∈ Rm×n
Y ∈ Rm×
In the previous example
X ∈ R2×1 =
1
2
A ∈ R2×2 =
1 0
0 2
Y ∈ R2×1 =
1
4
7

8. Understanding the Measurement Matrix
If we think of how matrix multiplication works, each row of the
measurement matrix is a measurement.
1 0
0 2
1
2
=
1(1) + 0(2)
0(1) + 2(2)
=
1
4
8

9. Compressed Sensing
Real Problem in Signal Processing: Measurement
Is there a better way to recover the original data with fewer
measurements?
What are the fewest number of measurements we need to recover
the original signal?
9

10. Compressed Sensing
We can recover matrices but NOT with traditional linear algebra
techniques.
A becomes a nonsquare matrix.
Not invertible
Underdetermined System of Equations where m < n
a1,1x1 + a1,2x2 + · · · + a1,nxn = c1
a2,1x1 + a2,2x2 + · · · + a2,nxn = c2
...
...
...
am,1x1 + am,2x2 + · · · + am,nxn = cm
10

11. Compressed Sensing
We can recover matrices but NOT with traditional linear algebra
techniques.
A becomes a nonsquare matrix.
Not invertible
Underdetermined System of Equations where m < n
a1,1x1 + a1,2x2 + · · · + a1,nxn = c1
a2,1x1 + a2,2x2 + · · · + a2,nxn = c2
...
...
...
am,1x1 + am,2x2 + · · · + am,nxn = cm
Pseudoinverse
The pseudoinverse A† is defined as A† = (ATA)−1AT where AT is the
transpose of A.

12. Sparsity Assumption
Definition: Jointly k-sparse Matrix
A matrix A is jointly k-sparse if there exist no more than k rows in A
that have nonzero entries. For example:






1 3 0
2 −1 2
0 0 0
0 0 0
5 2 −6






A 3-sparse matrix




0 0 0
2 −4 −2
0 9 2
4 1 1




A 3-sparse matrix
12

13. Sparsity Assumption
Definition: Jointly k-sparse Matrix
A matrix A is jointly k-sparse if there exist no more than k rows in A
that have nonzero entries. For example:






1 3 0
2 −1 2
0 0 0
0 0 0
5 2 −6






A 3-sparse matrix




0 0 0
2 −4 −2
0 9 2
4 1 1




A 3-sparse matrix
Many matrices are well approximated by k-sparse matrices after a
change of basis.
13

14. Sparsity Assumption
Definition: Jointly k-sparse Matrix
A matrix A is jointly k-sparse if there exist no more than k rows in A
that have nonzero entries. For example:






1 3 0
2 −1 2
0 0 0
0 0 0
5 2 −6






A 3-sparse matrix




0 0 0
2 −4 −2
0 9 2
4 1 1




A 3-sparse matrix
We assume k , which means the rank of X is determined by its
column space.
14

15. Compressed Sensing
Theorem: Donoho 2004, Candes and Tao 2004
Using randomness in matrix A we can recover the signal X where X
is a k-sparse matrix at a fraction of measurements.
15

16. Decoding Algorithms
Algorithm 1 Thresholding
Input: A, Y, k
Output: A k-sparse approximation of ˆX of the target signal X
16

17. Decoding Algorithms
Algorithm 1 Thresholding
Input: A, Y, k
Output: A k-sparse approximation of ˆX of the target signal X
1: X = A∗Y (rough approximation of the inverse)
17

18. Decoding Algorithms
Algorithm 1 Thresholding
Input: A, Y, k
Output: A k-sparse approximation of ˆX of the target signal X
1: X = A∗Y (rough approximation of the inverse)
2: T = PrincipalSupportk(X) (estimate for support set)
18

19. Decoding Algorithms
Algorithm 1 Thresholding
Input: A, Y, k
Output: A k-sparse approximation of ˆX of the target signal X
1: X = A∗Y (rough approximation of the inverse)
2: T = PrincipalSupportk(X) (estimate for support set)
3: ˆX = A†
TY (projection onto k subspace defined by T)
19

20. Thresholding
20

21. Thresholding
21

22. Thresholding
22

23. Thresholding
23

24. Thresholding Coherence
Thereom: Thresholding
Let A ∈ Rm×n be a matrix with entries drawn i.i.d from N(0, m−1)
and let X ∈ Rn× be a jointly k-sparse matrix. Let Y ∈ Rm× be a
matrix such that Y = AX. If µ is the coherence of A, then the
Thresholding Algorithm can recover the jointly k-sparse matrix X
from matrices Y and A as long as
k <
1
2
µ−1
2ν∞ + 1 − 1
where ν∞ is defined as
ν∞ =
mini∈S ||x(i)||2
2
r
=1
||x ||2
∞
.

25. Thresholding Coherence
Corollary
The Thresholding Algorithm recovers a jointly k-sparse matrix
X ∈ Rn× as long as
m >
4k2
2ν∞ + 1

26. Rank Aware Thresholding
Algorithm 2 Rank Aware Thresholding
Input: A, Y, k
Output: A k-sparse approximation of ˆX of the target signal X
26

27. Rank Aware Thresholding
Algorithm 2 Rank Aware Thresholding
Input: A, Y, k
Output: A k-sparse approximation of ˆX of the target signal X
1: U = orth(Y) (U is an orthogonal basis of the columns of Y)
27

28. Rank Aware Thresholding
Algorithm 2 Rank Aware Thresholding
Input: A, Y, k
Output: A k-sparse approximation of ˆX of the target signal X
1: U = orth(Y) (U is an orthogonal basis of the columns of Y)
2: X = A∗U (rough approximation of the inverse)
3: T = PrincipalSupportk(X) (estimate for support set)
4: ˆX = A†
TY (projection onto k subspace defined by T)

29. Rank Aware Thresholding
Thereom (BLW): Rank Aware Thresholding
Let A ∈ Rm×n be a matrix with entries drawn i.i.d from N(0, m−1)
and let X ∈ Rn× be a jointly k-sparse matrix. Let Y ∈ Rm× be a
matrix such that Y = AX. We define the matrix U ∈ Rm× to be a
matrix with orthogonal columns where there exist matrices Σ and V
such that UΣVT is the singular value decomposition of Y. Then the
Rank Aware Thresholding Algorithm can recover the matrix X from
the matrices Y and A with probability 1 − δ as long as
δ (n − k)e−C(mν2r/k−4r)
where
ν2 =
mini∈S ||A∗U||2
2
maxi∈S ||A∗U||2
2
.

30. Rank Aware Thresholding
Corollary
The Rank Aware Thresholding Algorithm correctly selects the
support of a jointly k-sparse matrix X ∈ Rn× if
m
Ck
ν2
1 +
1
r
ln
n
δ

31. Rank Aware Thresholding
Corollary
The Rank Aware Thresholding Algorithm correctly selects the
support of a jointly k-sparse matrix X ∈ Rn× if
m
Ck
ν2
1 +
1
r
ln
n
δ
Importance of Corollary:
m ∼ Ck

32. Rank Aware Thresholding
Corollary
The Rank Aware Thresholding Algorithm correctly selects the
support of a jointly k-sparse matrix X ∈ Rn× if
m
Ck
ν2
1 +
1
r
ln
n
δ
Importance of Corollary:
m ∼ Ck
Eliminates the “square-root bottleneck"

33. Rank Aware Thresholding
Corollary
The Rank Aware Thresholding Algorithm correctly selects the
support of a jointly k-sparse matrix X ∈ Rn× if
m
Ck
ν2
1 +
1
r
ln
n
δ
Importance of Corollary:
m ∼ Ck
Eliminates the “square-root bottleneck"
Thresholding Corollary
The Thresholding Algorithm recovers a jointly
k-sparse matrix X ∈ Rn× as long as
m >
4k2
2ν∞ + 1

34. Rank Aware Thresholding
Corollary
The Rank Aware Thresholding Algorithm correctly selects the
support of a jointly k-sparse matrix X ∈ Rn× if
m
Ck
ν2
1 +
1
r
ln
n
δ
Importance of Corollary:
m ∼ Ck
Eliminates the “square-root bottleneck"
Thresholding Corollary
The Thresholding Algorithm recovers a jointly
k-sparse matrix X ∈ Rn× as long as
m >
4k2
2ν∞ + 1

35. Rank Aware Thresholding
Corollary
The Rank Aware Thresholding Algorithm correctly selects the
support of a jointly k-sparse matrix X ∈ Rn× if
m
Ck
ν2
1 +
1
r
ln
n
δ
Importance of Corollary:
m ∼ Ck
Eliminates the “square-root bottleneck"
Tells us how many measurements we need to recover a jointly
k-sparse signal

36. Rank Aware Thresholding
Corollary
The Rank Aware Thresholding Algorithm correctly selects the
support of a jointly k-sparse matrix X ∈ Rn× if
m
Ck
ν2
1 +
1
r
ln
n
δ
Importance of Corollary:
m ∼ Ck
Eliminates the “square-root bottleneck"
Tells us how many measurements we need to recover a jointly
k-sparse signal
Rank Aware Thresholding is actually rank aware
36

37. Thresholding Algorithm (rank = 5)
37

38. Thresholding Algorithm (rank = 20)
38

39. Thresholding Algorithm (rank = 32)
39

40. Rank Aware Thresholding Algorithm (rank = 5)
40

41. Rank Aware Thresholding Algorithm (rank = 20)
41

42. Rank Aware Thresholding Algorithm (rank = 32)
42

43. Modeling Process
Modeling Process
Predict the behavior of decoding algorithms for problems with
large dimensions

44. Modeling Process
Modeling Process
Predict the behavior of decoding algorithms for problems with
large dimensions
New model

45. Modeling Process
Modeling Process
Predict the behavior of decoding algorithms for problems with
large dimensions
New model
Typical tests are problems on the scale 27
or 28
.

46. Modeling Process
Modeling Process
Predict the behavior of decoding algorithms for problems with
large dimensions
New model
Typical tests are problems on the scale 27
or 28
.
We want to know behavior of problems at least 212
.

47. Modeling Process
Modeling Process
Predict the behavior of decoding algorithms for problems with
large dimensions
New model
Typical tests are problems on the scale 27
or 28
.
We want to know behavior of problems at least 212
.
Hard to run many tests of this size.

48. Modeling Process
Modeling Process
Predict the behavior of decoding algorithms for problems with
large dimensions
New model
Typical tests are problems on the scale 27
or 28
.
We want to know behavior of problems at least 212
.
Hard to run many tests of this size.
Model the region of the 50% Success Curve

49. Modeling Process
Modeling Process
Predict the behavior of decoding algorithms for problems with
large dimensions
New model
Typical tests are problems on the scale 27
or 28
.
We want to know behavior of problems at least 212
.
Hard to run many tests of this size.
Model the region of the 50% Success Curve
Relate 50% Success Curve and Fraction of Correct Support

50. 50% Success and Fraction of Correct Support
50

51. 50% Success and Number of Missed Entries
51

52. 50% Success and Number of Missed Entries
52

53. 50% Success and Number of Missed Entries
53

54. 50% Success and Number of Missed Entries
54

55. Modeling Thresholding
55

56. Modeling Rank Aware Thresholding
56

57. 57

58. Iterative Algorithms
Examples of Iterative Algorithms in Compressed Sensing
Orthogonal Matching Pursuit (OMP)
Compressive Sampling Matching Pursuit (CoSaMP)
Iterative Hard Thresholding (IHT)
Normal Iterative Hard Thresholding (NIHT)
Conjugate Gradient Iterative Hard Thresholding (CGIHT)
58

59. OMP
Algorithm 3 Orthogonal Matching Pursuit (OMP)
Input: A, y, k
Output: A k-sparse approximation of ˆx of the target signal x
Initialization: Set x0 = 0, r0 = y, T0 = {}.
Iteration:
1. for j = 1, 2, . . . , k
2. i = argmax |A∗rj−1| (identify column of A most correlated to residual)
3. Tj = Tj−1 ∪ {i} (add the new column index to the index set)
4. xj = A†
Tj y (project the measurements onto the T subspace)
5. rj = y − Axj (update the residual)
6. end for
7. return ˆx = xk (return the k-sparse vector xk
)
59

60. CoSaMP
Algorithm 4 Compressive Sampling Matching Pursuit (CoSaMP)
Input: A, y, k
Output: A k-sparse approximation of ˆx of the target signal x
Iteration:
1. Tn = {indices of the largest 2k in modulus entries of A∗(y − Axn) }
2. Un = Tn ∪ Sn where Sn = supp(xn)
3. un = argmin{||y − Az||2, supp(z) ⊆ Un}
4. xn+1 = Hs(un) where Hs keeps the largest k rows of un
60

61. Iterative Algorithms
61

62. Conjecture
1 We know Thresholding in Rank Aware

63. Conjecture
1 We know Thresholding in Rank Aware
2 We know OMP and CoSaMP are Rank Aware

64. Conjecture
1 We know Thresholding in Rank Aware
2 We know OMP and CoSaMP are Rank Aware
3 We know OMP and CoSaMP contain Thresholding at every
iteration

65. Conjecture
1 We know Thresholding in Rank Aware
2 We know OMP and CoSaMP are Rank Aware
3 We know OMP and CoSaMP contain Thresholding at every
iteration
Conjecture
The rank awareness of OMP and CoSaMP comes from the
Thresholding step in their implementation
65

66. Modeling Iterative Algorithms
We want to model the iterative algorithms like we modeled
Thresholding
If this approach works for OMP and CoSaMP then we have
evidence supporting our conjecture
66

67. Modeling OMP
67

68. Modeling CoSaMP
68