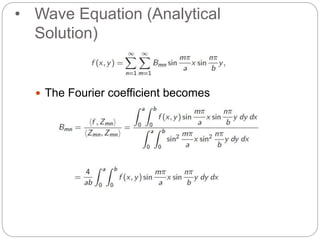
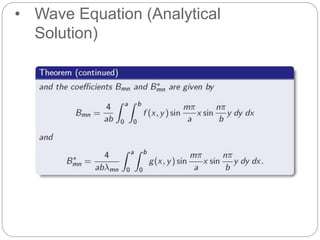
The document discusses simulating the two-dimensional wave equation using MATLAB, outlining both analytical and numerical solutions. It includes methods such as separation of variables, boundary and initial conditions, as well as stability conditions for numerical implementations. The process also integrates Fourier series and coding aspects to validate the solutions.

1. SIMULATION USING MATLAB
2-Dimensional Wave Equation
• Ahmed Hashem
• Ahmed Radwan
• Amr Mousa
• Hazem Hamdy
• Yomna Hamza
BY

2. • Our Goal

3. • Wave Equation (Analytical
Solution)
• Boundary conditions
• Initial Conditions
 Using separation of variables, the analytical
solution for the following equation goes as follows

4.  Dividing both sides by X(x)Y(y)T(t):
• Wave Equation (Analytical
Solution)

5.  The boundary conditions become:
 Using the conditions and solving for X(x) and
Y(y), we get the non-trivial solutions
(eigenfunctions)
with eigenvalues
• Wave Equation (Analytical
Solution)

6.  Solving for T(t), where
((eigenvalues)
 Our final solution becomes,
• Wave Equation (Analytical
Solution)

7.  The general solution becomes
 We then use the 2 initial conditions to obtain the 2
constants
(double Fourier
series)
• Wave Equation (Analytical
Solution)

8.  Using orthogonality,
• Wave Equation (Analytical
Solution)

9.  The Fourier coefficient becomes
• Wave Equation (Analytical
Solution)

10.  The general solution of the two dimensional wave
equation is then given by the following theorem:
• Wave Equation (Analytical
Solution)

11. • Wave Equation (Analytical
Solution)

12.  Back to the original problem
 Using centred difference in space and time, the
equation becomes
• Wave Equation (Numerical
Solution)

13.  Isolating the term that marches in time, we get
• Wave Equation (Numerical
Solution)
 Stability condition (where c2 =1) :
By optimizing the problem : Cmax was found to
equal 1

14.  Expressing the boundary conditions using our
new notation, we get:
 Starting from m=2, we iterate for every i and j in
our mesh
 Now, we code!
• Wave Equation (Numerical
Solution)

15. NOW, Let’s test the
program

16. References
 Daileda, R. (2012, March 1). The two
dimensional wave equation. Lecture
presented at Partial Differential Equations in
Trinity University, San Antonio, Texas.
 Haberman, R. (n.d.). Finite Difference
Numerical Methods for Partial Differential
Equations. In Applied Partial Differential
Equations (Fifth ed.). Pearson.