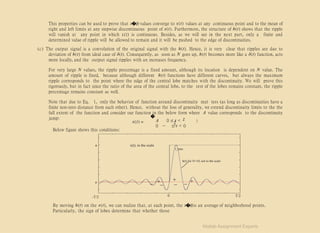
The document discusses various problems related to signal processing, including waveforms, filtering, and the Gibbs phenomenon in Fourier analysis. It outlines assignments that require working with MATLAB to analyze filter responses, impulse responses, and the effects of truncating Fourier series on waveforms. The document emphasizes understanding the mathematical principles behind these concepts and their practical implications in signal processing.

1. Signal Processing Continuous and Discrete
For any help regarding Matlab Assignment Help
visit : https://www.matlabassignmentexperts.com/,
Email - info@matlabassignmentexperts.com
or call us at - +1 678 648 4277
Matlab Assignment Experts

2. 0 10
-5 0 0 -1 0 0 5 0 0  ( ra d / s
Problem 1: A waveform f (t) with a real even spectrum F (jΩ)
F ( j 

1
 c  c  ( ra d / s
is filtered by an ideal band-pass filter with a purely real frequency response H(jΩ)
H ( j 
-4 0 0 -2 0 0 2 0 0 4 0 0  ( ra d / s
Determine the filter response y(t). Is this a causal filter?
Problem 2: Find the impulse response of an ideal high-pass filter, with cut-off frequency Ωc:
H ( j 
Problem
Matlab Assignment Experts

3. ( a ) N = 1 5 ( b) N = 3 1 ( c ) N = 6
Gibb’s phenomenon was the subject of much discussion in the mathematical literature around 1900, and in fact was cited as a
reason why Fourier analysis/synthesis did not work! The great mathematicians of the time did not understand what was going
on. You, however, do understand it and your task is to explain the phenomenon.
2
Hints: Feel free to do this any way you wish, but you may find it useful to consider H(jΩ) as a superposition of functions
with known FT relationships. In particular, the solution of Prob. 5 in PS 1 might be useful and/or the following bits and
pieces from the Frequency Domain class handout: the Fourier transform of a unit step function (p. 32), the duality property,
the time shift property, time reversal property, linearity property, all might help you.
Problem 3: Use the Fourier transform of a sinusoid (p. 34 of the class handout) to express the Fourier series representation of
a periodic waveform
∞
Σ
n 0 n
x(t) = A sin (nΩt + φ )
n = 0
as a Fourier transform.
Problem 4: Gibb’s phenomenon is associated with the synthesis of periodic waveforms with sharp (jump) discontinuities using a
truncatedFourier series. Consider a periodic waveform xp(t) and its Fourier series
∞
0
j n Ω t
Σ
xp(t) = Xn e
n = −∞
1 � T/2
n
X = p
x (t)e 0
−j n Ω t
dt
T −T/2
and let N
Xn ej n Ω 0 t
x (t) =
Þp,N
Σ
n = −N
be an approximation generated by truncating the series. It was observed in the late 1800’s that a finite series approximation
created a ripple in the synthesized waveform in the region of a jump discontinuity in xp(t), and that although the width of the
ripple decreased as more terms were included, the amplitude remained constant. The phenomenon was found to be
Þ p,N
present for any finite N. The figure below shows the synthesis of a square wave x (t) with
N = 15, 31, and 63.
Matlab Assignment Experts

4. -
(a) Explain the truncation of the series in the frequency domain as an ideal multiplicative filtering operation, and define the
filter pass-band.
(b) What is the equivalent time domain operation? OK - you win - it’s convolution, but the question is what are the two
functions being convolved? Write the appropriate convolution integral.
(c) Explain (i) why the height of the ripple on the square wave is constant for any finite series, and (ii) why the oscillatory
frequency increases as N increases.
Problem 5: An “all-pass”filter has a frequency response magnitude |H(jΩ)| that is a constant (ie is independent of
frequency Ω).
(a) Show that the first-order system with the pole-zero plot below is an all-pass filter.
j
s - p I a n
(b) Show that any system with (i) the same number of poles and zeros, (ii) with all poles in the left-half s-plane, and (iii)
the zeros mirror the poles about the imaginary axis, that is zi = −pi where x denotes the complex conjugate, is an all-pass
filter.
(c) Use MATLAB to plot (i) the frequency response, (ii) the impulse response, and (iii) the step response of the filter with a
pole and zero shown in (a) above. Choose an arbitrary gain constant.
(Some useful functions might be zpk(), t f ( ) , f r e q s ( ) , bode(), impulse(), step().)
(d) What useful purpose might an all-pass filter serve?
3
Matlab Assignment Experts

5. Solution of P r o b le m
Problem 1:
Y (jΩ) = H(jΩ)F (jΩ) and it is shown in the below figure
Y( jw)
10
1
2π
�
∞
y(t) = Y (j Ω
)ej Ω
t
dt
−∞
�
400
10
= ( ejΩt
dt +
2π 200
−
�2
0
0
ejΩt
dt)
−400
10
(e400j t
− e200j t
− e−400j t
+ e−200j t
)
= 2πj t
10
= (sin(400t) − sin(200t))
πt
It is not a casual filter (since y(t) = h(t)/5 and h(t) =
/ 0 for some t < 0).
Problem 2:
We define H∗(jΩ) = 1 − H(jΩ). Then H∗(jΩ) is a low pas filter, matching Prob. 5 in PS 1, which we have already found
it’simpulse response:
H (j Ω
) = 1 − H ∗
(j Ω
)
F −1 (H (j Ω
)) = F −1 (1) − F −1 (H ∗
(j Ω
))
h(t) = δ(t) − h∗(t)
h(t) = δ(t) − sin(Ωct)
πt
Matlab Assignment Experts

6. Problem 3:
Σ∞ Σ∞
x(t) = An sin(nΩ
0t + φn) = An (sin(nΩ
0t) cos φn + cos(nΩ
0t) sin φn)
n=0 n=0
x
�
(t) = x(t) ⊗ h(t) =
x
�
(t) =
� T
�
x
�
(t) =
n= 0
Σ∞
Σ∞
X (j Ω
) = An( F (sin(nΩ
0t)) cos φn + F (cos(nΩ
0t)) sin φn)
X(jΩ) = An (cos φn (−jπ (δ(Ω − nΩ0) − δ(Ω + nΩ0))) + sin φn (π (δ(Ω − nΩ0) + δ(Ω + nΩ0))))
n= 0
Σ∞
X(jΩ) = −jπ An ((cos φn + j sin φn) (δ(Ω − nΩ0) + (− cos φn + j sin φn) (δ(Ω + nΩ0))
n= 0
Σ∞ � �
X (j Ω
) = −j π An ej φn δ(Ω− nΩ
0) − e−j φn δ(Ω+ nΩ
0)
n=0
Problem 4:
(a) The ideal multiplicative filtering operation is a low pass filtering with the pass-band
Ω
c = N Ω
0: � 1 |n| ≤ N , |Ω
| ≤ Ω
c
0 |n| > N , |Ω
| > Ω
c
X
�
n = X nHn
n
H =
(b) It’
s a convolution in this specific form:
1
T
�T 2
x(τ )h(t − τ )dτ
—T
2
We can prove that why convolution is in this specific integral form for our Periodic Exponential Fourier Transform:
�T
� 0
jnΩ t
�
Σ∞ Σ∞
x�(t) = XnHne =
2
0
−jnΩ τ jnΩ t
� � � �
Xn
h(τ )e 0
dτ e
1
T —T
n=−∞
� T
�
n=−∞ 2
Σ∞ �
Σ∞
0
j nΩ (t−τ )
�
�
�
Xne −jnΩ τ jnΩ t
�
0
e 0
�
Xne
2 2
h(τ )
1
T −T
dτ = h(τ )
1
T −T
dτ
n=−∞ n=−∞
2 2
1
T
�T 2
h(τ )x(t − τ )dτ
—T
2
We can also find the specific form of our filter:
Σ∞ ΣN
HnejnΩ0t
=
h(t) =
n=−∞ n=−N
ΣN ΣN
ej nΩ
0t
= 1 + 2 cos (nΩ
0t) = −1 + 2 cos (nΩ
0t)
n=1 n=0
Matlab Assignment Experts

7. Here we use below trigonometric relation to simplify our summation, where ϕ = 0 and
α = Ω0t:
� �
sin (n+ 1)α 2
2
·cos (ϕ + nα
)
cos ϕ + cos (ϕ + α) + cos (ϕ + 2α) + ···+ cos (ϕ + nα) =
sin α
2
� �
(N + 1)Ω
0t
2
sin 2
·cos ( N Ω
0t
)
sin Ω
0t
ΣN
h(t) = −1 + 2 cos (nΩ
0t) = −1 + 2
n=0
2
Then we use below trigonometric relation to simplify our impulse response:
2 sin θcos ϕ = sin(θ + ϕ) + sin(θ − ϕ)
sin
� �
(N + 1)Ω
0t
2
2
0
N Ω t
·cos ( ) 0
� �
sin (N + 1
)Ωt + sin ( Ω
0t
)
h(t) = −1 + 2 = −1 + 2 2
sin Ω0t
sin Ω
0t
2 2
�
sin (N + 1 )Ω
0t
�
h(t) = 2
sin Ω0t
2
Here we further analyze this h(t) function, so we can use its properties for the next part of the problem:
Note that for small t values, h(t) can be approximated to:
sin (N + 1 )Ω
0t
� �
t → 0 ⇒ h(t) → 2
Ω0t
2
πt
The value of h(t) |t→0 , for large N values, is very close to h∗ = sin (N Ωt)
which can be 0
obtained for a Continuous Fourier Transform of a Low Pass Filter with Ωc= NΩ0. Hence, in the vicinity of t = 0,
h(t) acts like a sinc function (with the maximum value
2
of 2N + 1), but as soon as it gets close to its boundaries (|t| ≤ T ⇒ |Ω0t| ≤ π), it
oscillates quickly with Ω= (N + 0.5)Ω0 around −1 and +1.
Note that for the Continuous Fourier Transform, we expect a h∗(t); where it is to t
be evaluated between −∞ to +∞ and contained with an envelope in the form of 1 .
On the other hand, for our case of Periodic Fourier Transform, h(t) it is to be evaluated between −T to + T and is also
periodic. 2 2
Note that for any N value, if x(t) ≡ 1 then x�(t)≡ 1 which means that following relation holds for any N:
1 = 1
T
2
—T
h(τ )dτ = 2
T
�T � T 2
0
h(τ )dτ
2
Furthermore, for very large N values, the h(t) function become very narrow, and hence above integral can be
approximated to the integration around any finite, non-zero interval around t = 0:
T 1 � t∗ � T
2
∗ ∗
(Eq. 1) N → ∞ ⇒ ∀
t s.t. 0 < t ≤ : h(τ )dτ → h(τ )dτ
2 T
1
T
0 0
Matlab Assignment Experts

8. This properties can be used to prove that x�(t) values converge to x(t) values at any continuous point and to the mean of
right and left limits at any stepwise discontinuous point of x(t). Furthermore, the structure of h(t) shows that the ripple
will vanish at any point in which x(t) is continuous. Besides, as we will see in the next part, only a finite and
determined value of ripple will be allowed to remain and it will be pushed to the edge of discontinuities.
(c) The output signal is a convolution of the original signal with the h(t). Hence, it is very clear that ripples are due to
deviation of h(t) from ideal case of δ(t). Consequently, as soon as N goes up, h(t) becomes more like a δ(t) function, acts
more locally, and the output signal ripples with an increases frequency.
For very large N values, the ripple percentage is a fixed amount, although its location is dependent on N value. The
amount of ripple is fixed, because although different h(t) functions have different curves, but always the maximum
ripple corresponds to the point where the edge of the central lobe matches with the discontinuity. We will prove this
rigorously, but in fact since the ratio of the area of the central lobe, to the rest of the lobes remains constant, the ripple
percentage remains constant as well.
Note that due to Eq. 1, only the behavior of function around discontinuity mat ters (as long as discontinuities have a
finite non-zero distance from each other). Hence, without the loss of generality, we extend discontinuity limits to the the
full extent of the function and consider our function in the below form where A value corresponds to the discontinuity
jump:
x(t) = T 2
�
A 0 ≤ t < T
0 − ≤ t < 0
2
Below figure shows this conditions:
A
0

 
   
h(t) for N=10, not to the scale
x(t), to the scale
t_max
0 T/2
-T/2
By moving h(t) on the x(t), we can realize that, at each point, the x�(t)is an average of neighborhood points.
Particularly, the sign of lobes determine that whether those
Matlab Assignment Experts

9. point have a positive or negative contribution. Since, major contribution comes from the central lobes, we can guess
that the maximum ripple occurs when the edge of cen tral lobe match with t = 0. In that case, the next negative lobe
cannot decrease the x�(t) value and we have a maximum ripple. The next maxima and minima of ripples also
correspond to other lobe edges touching t = 0.
Now we prove this rigorously. For our specific case of x(t), and our even h(t) function, we can simplify the convolution
integral: −t
2 2
� T � T � T
2
x
�
(t) = h(t − τ )x(τ )dτ = A
T 0
h(t − τ )dτ = A
T
1
T −T
−t
h(τ )dτ
2
dx
�
(t) T
= −h( − t) + h(t)
dt 2
We are interested in 0 < t << T , and hence dx
b(t)
≈ h(t). Consequently, maxi
2 dt
2
mum/minimum values correspond to (N + 1
)Ω0tmax/min = kπ such that 0 < k << N.
max
The highest maximum corresponds to the t = π = T . Now we compute
1 1
(N + 2 )Ω
0 2(N + 2 )
the x�(tmax) value by breaking the original integral to two parts:
A −t max
1 1 −t max
�T � 0
2
�T
2
x
�
(tmax) =
T
h(τ )dτ = A(
T
h(τ )dτ +
T
h(τ )dτ )
−tmax −tmax 0
Now note that for large N values from Eq. 1 we can conclude that:
1
T
−t max
�T � T
2 2
h(τ )dτ ) = 1
T
h(τ )dτ ) =
0 0
Also for the other part of integral, τ is very close to zero and we can simplify h(t) with
2
a sinc form and also change integration variable by θ = (N + 1
)Ω0t:
�
1 0
�
1 0 sin ((N + 1
)Ωτ )
�
1 0
sin θ 2
�π
1 sin θ
T −t max T −t max
Ω
0τ
2
h(τ )dτ) = 2 0
dτ =
−π
T θ Ω0
dθ =
π 0 θ dθ
θ
A short survey of literature or a Taylor expansion of sin θ
ends to:
dθ = + 0.089490...
0
π θ 2
�
1 π
sin θ 1
Hence the maximum ripple corresponds to:
1 1
x�(tmax) = A(
2
+
2
+ 0.089490...) = A(1 + 0.089490...)
1
2
This corresponds to about 9% overshoot and this overshoot is only dependent on the local discontinuity jump and
independent of N or specific form of x(t). Other proofs, for less general cases, could also be found in the Wikis.
Matlab Assignment Experts

10. Problem 5:
(a) s − 3
H(s) = K
s + 3
�
|H (j Ω
)| = |K |�
�
�
j Ω− 3� �
= |K |
�
j Ω+ 3�
(b) Consider this pole-zero plot:
j
s -p I a
n
r
r
r
1 q
q
2
q
3
Let the vectors from the poles and zeros to an arbitrary test frequency Ωbe ri and qi:
|H (j Ω
)| = |K |
|q1||q2||q3|
= |K |
|r1||r1||r1|
since |qi| = |ri| for all i regardless of the system order. Therefore, this given pole-zero configuration, as well as all who
satisfy problem conditions, are all-pass filters.
(c) M AT LA B C om m and − line :
>> H_s=tf([1 -3], [1 3])
Transfer function: s - 3
s + 3
>> bode(H_s);
>> subplot(2,1,1)
Matlab Assignment Experts

11. >> step(H_s);
>> subplot(2,1,2)
>> impulse(H_s);
Bode Diagram
Magnitude
(abs)
1
0.8
0.6
0.4
0.2
0
180
135
90
45
Amplit
ude
Amplit
ude
Phase
(deg)
0
10−1
10
0
10
1
10
2
Frequency (rad/sec)
Step Response
0
1
0.5
0
−0.5
−1
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Time (sec)
Impulse Response
0
−2
−4
−6
−8
−10
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Time (sec)
(d) These filters are useful for manipulating the phase of the spectral components in a signal, without altering its
magnitude.
Matlab Assignment Experts