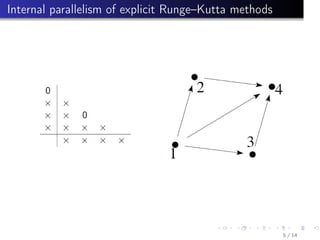
This document summarizes parallel numerical methods for solving ordinary differential equations (ODEs). It discusses two types of parallelism: across the system (space) and across the method (time). Predictor-corrector and Runge-Kutta methods are described that can exploit parallelism across time by parallelizing stages. Optimal Runge-Kutta methods use the minimum number of stages for a given order. Block methods solve ODE systems in parallel. Extrapolation and multiple shooting methods are also mentioned for parallelizing ODE solutions.

1. Parallel Numerical Methods for Ordinary Differential
Equations
S. I. Solodushkin1,2, I. F. Yumanova1
1 Ural Federal University
2 Institute of Mathematics and Mechanics
Ural HPC 2016, Ekaterinburg, Russia
2016, October 06.

2. The problem
y (x) = f (x, y(x)),
y(x0) = y0,
(1)
where x ∈ [x0; X], y ∈ Rm.
Gear classification:
1 parallelism across the system or, that is the same, parallelism across
the space;
2 parallelism across the method or, that is the same, parallelism across
the time.
2 / 14

3. Predictor-corrector type methods
W. L. MIRANKER AND W. LINIGER, Parallel methods for the numerical
integration of ordinary differential equations, Math. Comp., 91 (1967)
yp
n+1 = yc
n +
h
2
3f (xn, yc
n ) − f (xn−1, yc
n−1) ,
yc
n+1 = yc
n +
h
2
f (xn, yc
n ) + f (xn+1, yp
n+1) ,
(2)
yp
n+1 = yc
n−1 + 2hf (xn, yp
n ),
yc
n = yc
n−1 +
h
2
f (xn−1, yc
n−1) + f (xn, yp
n )) ,
(3)
3 / 14

4. Runge–Kutta methods
Consider an explicit s-stage Runge–Kutta method
k1 = f (xn, yn),
k2 = f (xn + c2h, yn + ha21k1),
k3 = f (xn + c3h, yn + h(a31k1 + a32k2)),
...
ks = f (xn + csh, yn + h(as1k1 + ... + as,s−1ks−1)),
yn+1 = yn + h(b1k1 + ... + bsks)
(4)
0
c2 a21
c3 a31 a32
...
cs as1 as2 ... as,s−1
b1 b2 ... bs−1 bs
k1 = f (xn, yn)
k2 = f (xn + h
2 , yn + h
2 k1)
k3 = f (xn + h
2 , yn + h
2 k2)
k4 = f (xn + h, yn + hk3)
yn+1 = yn + h
6 (k1 + 2k2 + 2k3 + k4)
4 / 14

5. Internal parallelism of explicit Runge–Kutta methods
5 / 14

6. Internal parallelism of explicit Runge–Kutta methods
Let us consider RK matrix A which could be partitioned (possibly after a
permutation of the stages) as







01
A21 02
A31 A32 03
...
...
...
Aσ1 Aσ2 . . . Aσ2 0σ







Theorem
For an explicit Runge–Kutta method with σ sequential stages
1) the order p σ for any number of available processors,
2) if p = σ, the stability region is z : | p
k=1
zk
k! | 1 .
6 / 14

7. Internal parallelism of implicit Runge–Kutta methods
Consider an implicit s−stage Runge–Kutta method
ki = f

xn + ci h, yn + h
s
j=1
aij kj

 , i = 1, ..., s
yn+1 = yn + h
s
i=1
bi ki ,
(5)







D1
A21 D2
A31 A32 D3
...
...
...
Aσ1 Aσ2 . . . Aσ2 Dσ







1/2 1/2 0 0 0
2/3 0 2/3 0 0
1/2 -5/2 5/2 1/2 0
1/3 -5/3 4/3 0 2/3
-1 3/2 -1 3/2
7 / 14

8. Optimal with respect to the order methods
Whether it is always possible to find ERK method of order p using not
more than p effective stages, assuming that suffucient number of
processors are available?
These methods are called P-optimal.
4 5 6 7 8 9 10
Sequential ERK
smin p 6 7 9 11 12 13
S p 5 6 7 8 9 10
Optimal RK
Seff p 6 7 9 11 12 13
Num. of proc - 3 3 4 4 5 5
8 / 14

9. Optimal with respect to the order methods
Method (5) can be interpreted as an ERK method with scheme
0 0
c A 0
c 0 A 0
...
...
...
c 0 0 0 A 0
0 . . . 0 0 bT
(6)
We assume that σ sequential stages are performed and s processors are
available.
Theorem
The parallel iterated Runge–Kutta method (5) in form (6) is of order
p = min(p0, σ), where p0 denotes the order of the basic method.
The choice σ = p0 yields P-optimal ERK methods.
9 / 14

10. How many processors do we need?
What is the least number of processors needed to implement an optimal
ERK method.
The basic method is the s-stage Gaussian–Legendre type RK method,
which has the smallest number of stages with respect to their order.
This allowed to construct the method of order p = 2s which is P-optimal
on s processors.
Van Der Houwen P. J., Sommeijer B. P. Parallel iteration of high-order Runge-Kutta
methods with stepsize control // Journal of Computational and Applied Mathematics,
1990. Volume 29. Issue 1. pp. 111–127.
10 / 14

11. Block methods
yn+1
yn+2
= h
2/3 −1/12
4/3 1/3
fn+1
fn+2
+
yn
yn
+ h
5/12
1/3
fn
fn
.
εn =
h4
24
u(4)
(ζn+1), −
h5
90
u(5)
(ζn+2)
Shampine L. F. and Watts H. A. Block Implicit One-Step Methods // Math. Comp.,
1969. V. 23. pp. 731–740.
11 / 14

12. Extrapolation methods
12 / 14

13. Multiple shooting algorithms
y0(x) = f (x, y0(x)), y1(x) = f (x, y1(x)), . . . yn−1(x) = f (x, yn−1(x)),
y0(0) = y0 y1(x1) = U1 yn−1(xn−1) = Un−1
matching conditions U1 = y0(x1), . . . , Un−1 = yn−2(xn−1),



U1 − y0(x1) = 0
U2 − y1(x2) = 0
. . .
Un−1 − yn−1(xn−1) = 0
Uk+1
0 = y0
Uk+1
i+1 = yi (xi+1, Uk
i ) +
∂yi (xi+1, Uk
i )
∂Ui
(Uk+1
i − Uk
i ), i = 0, 1, 2, . . . , n − 2
13 / 14

14. Thank you for attention
Parallel Numerical Methods for Ordinary Differential Equations:
a Survey
14 / 14