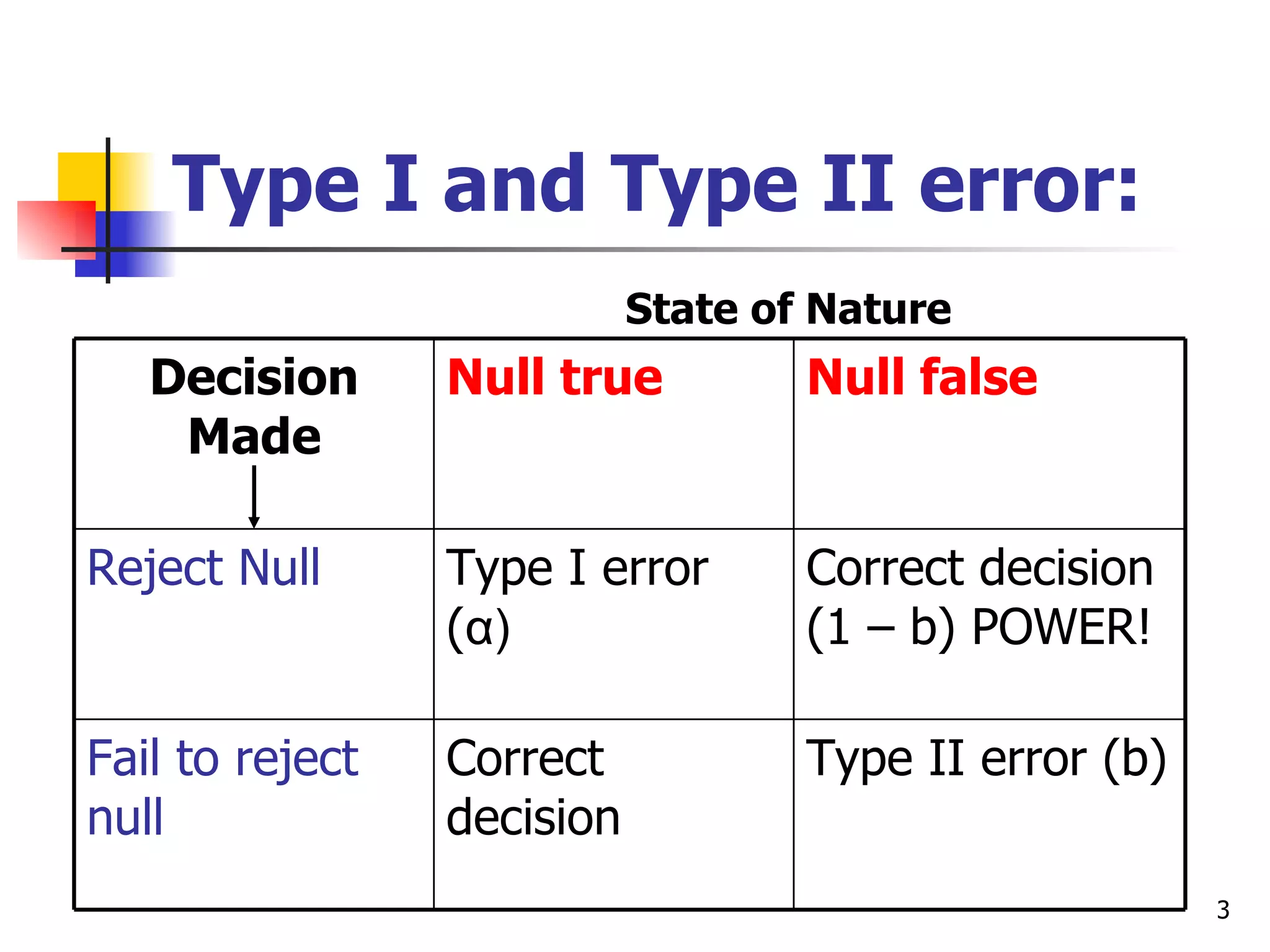
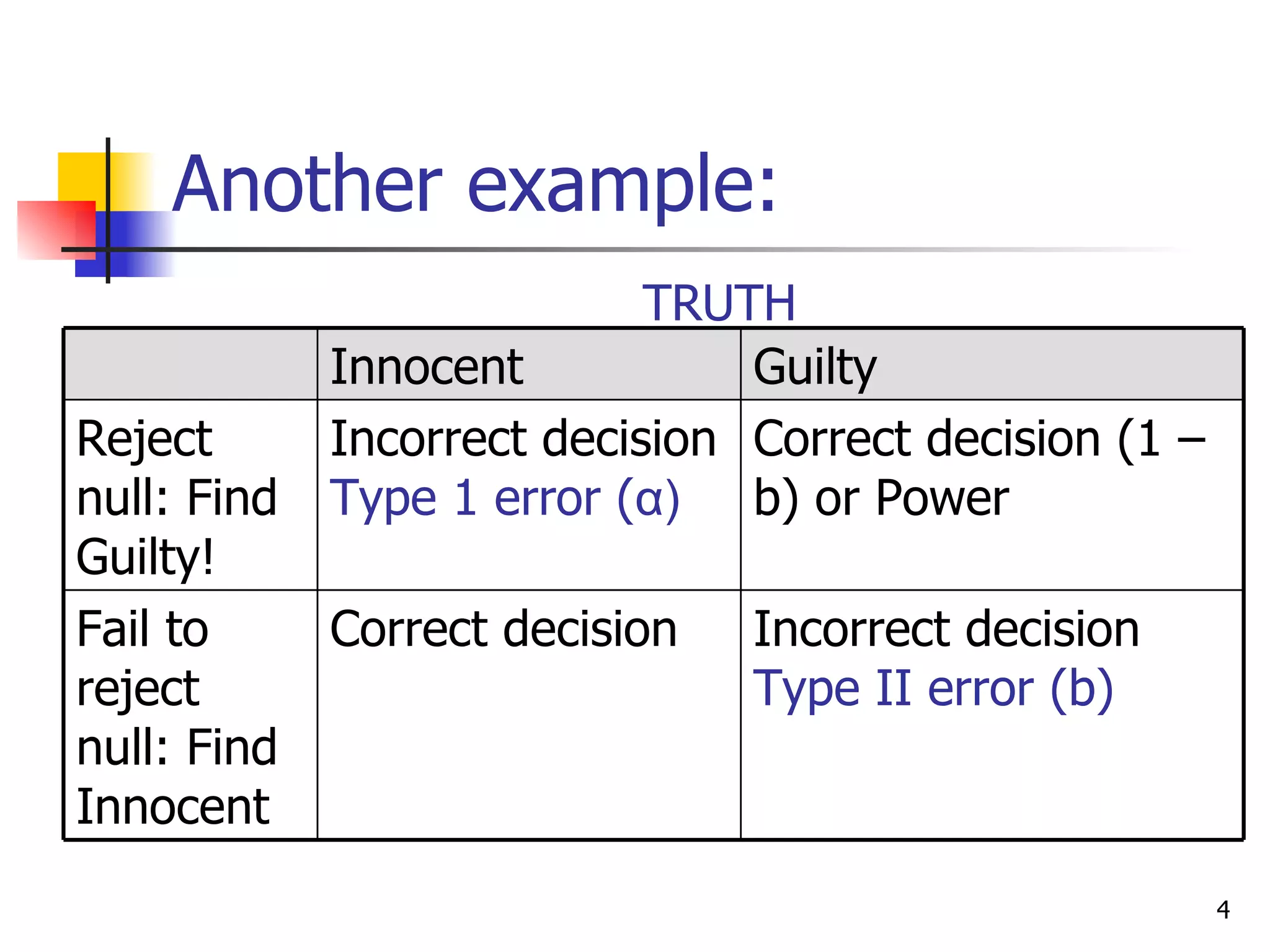
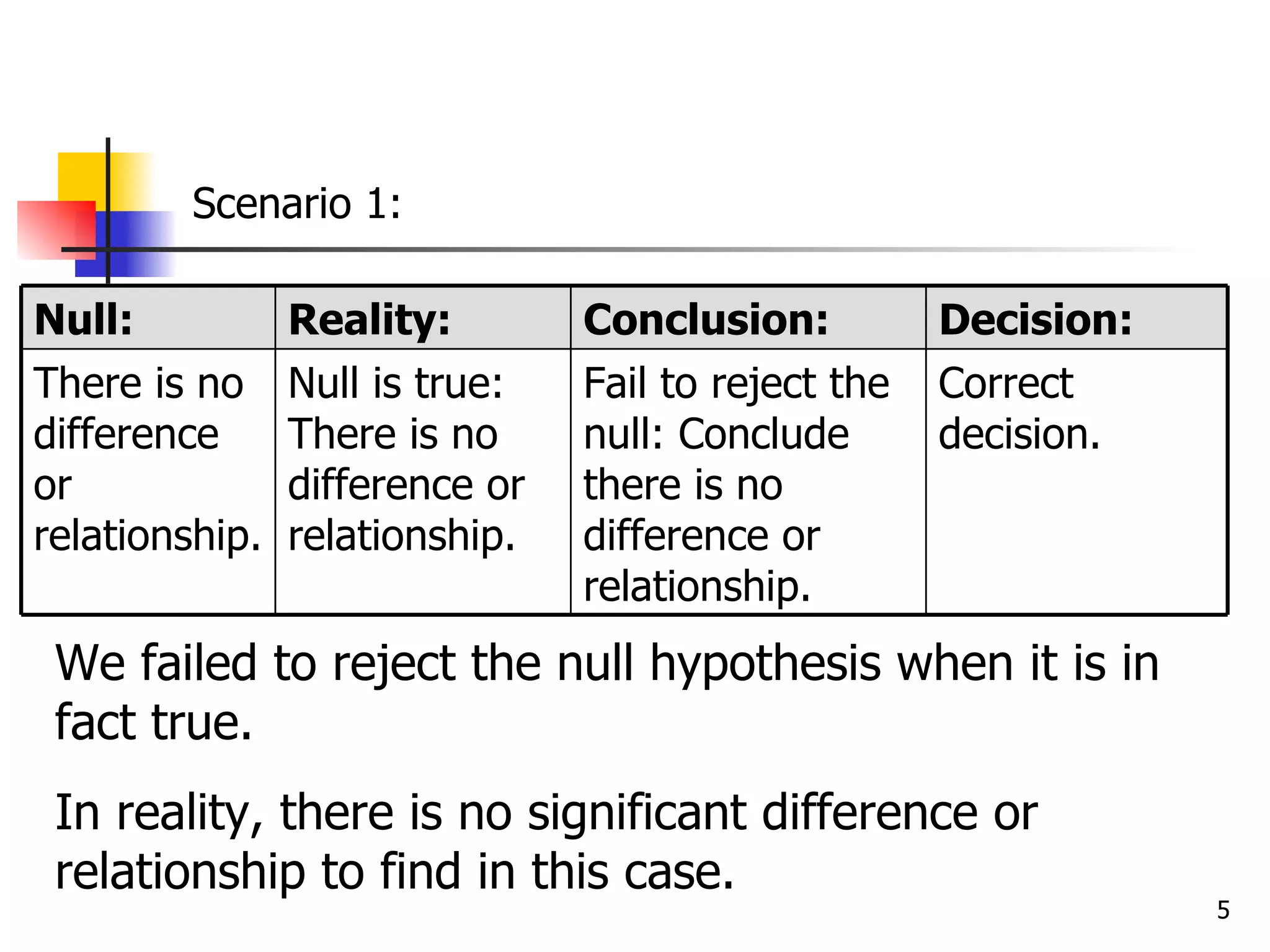
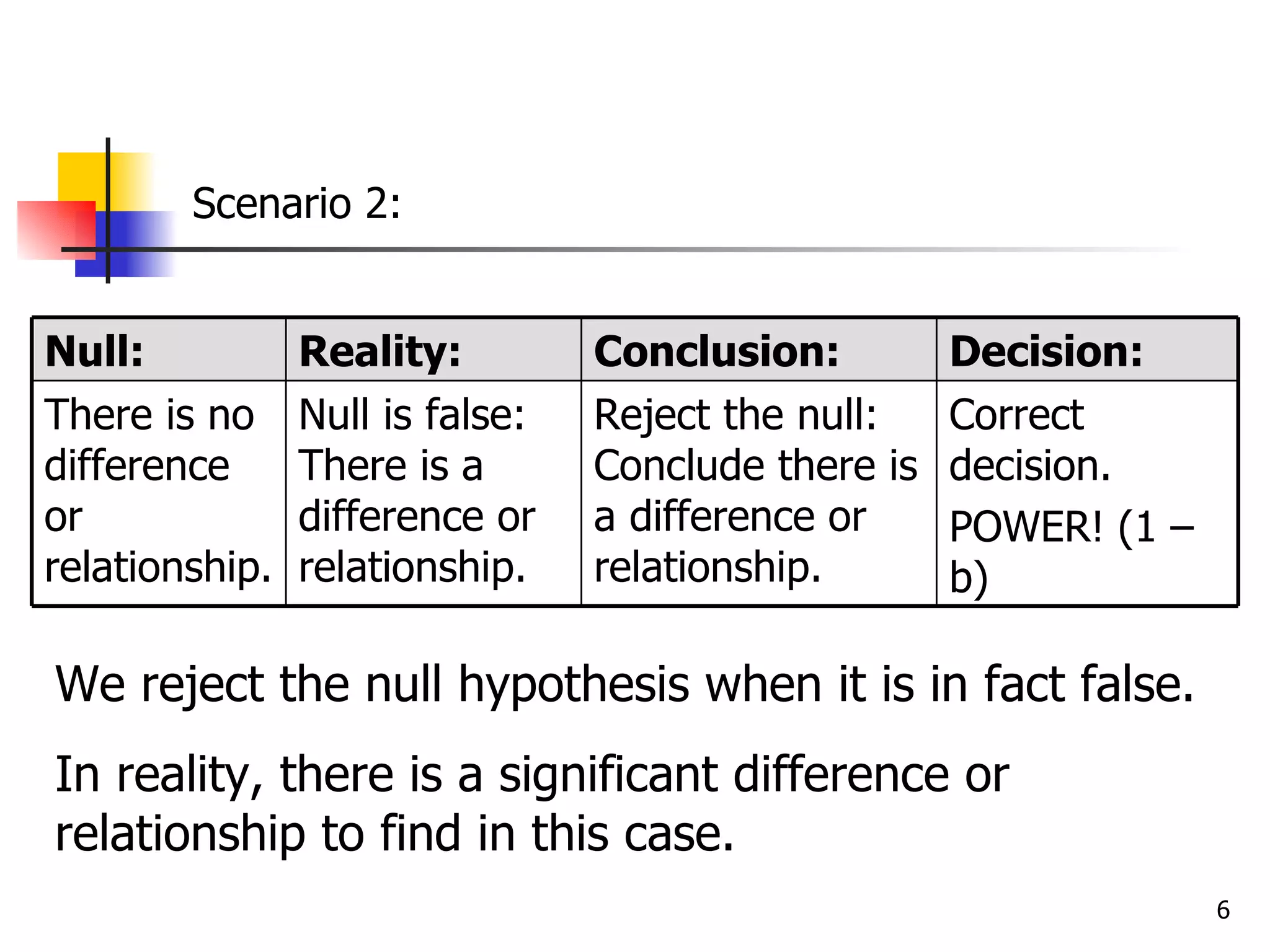
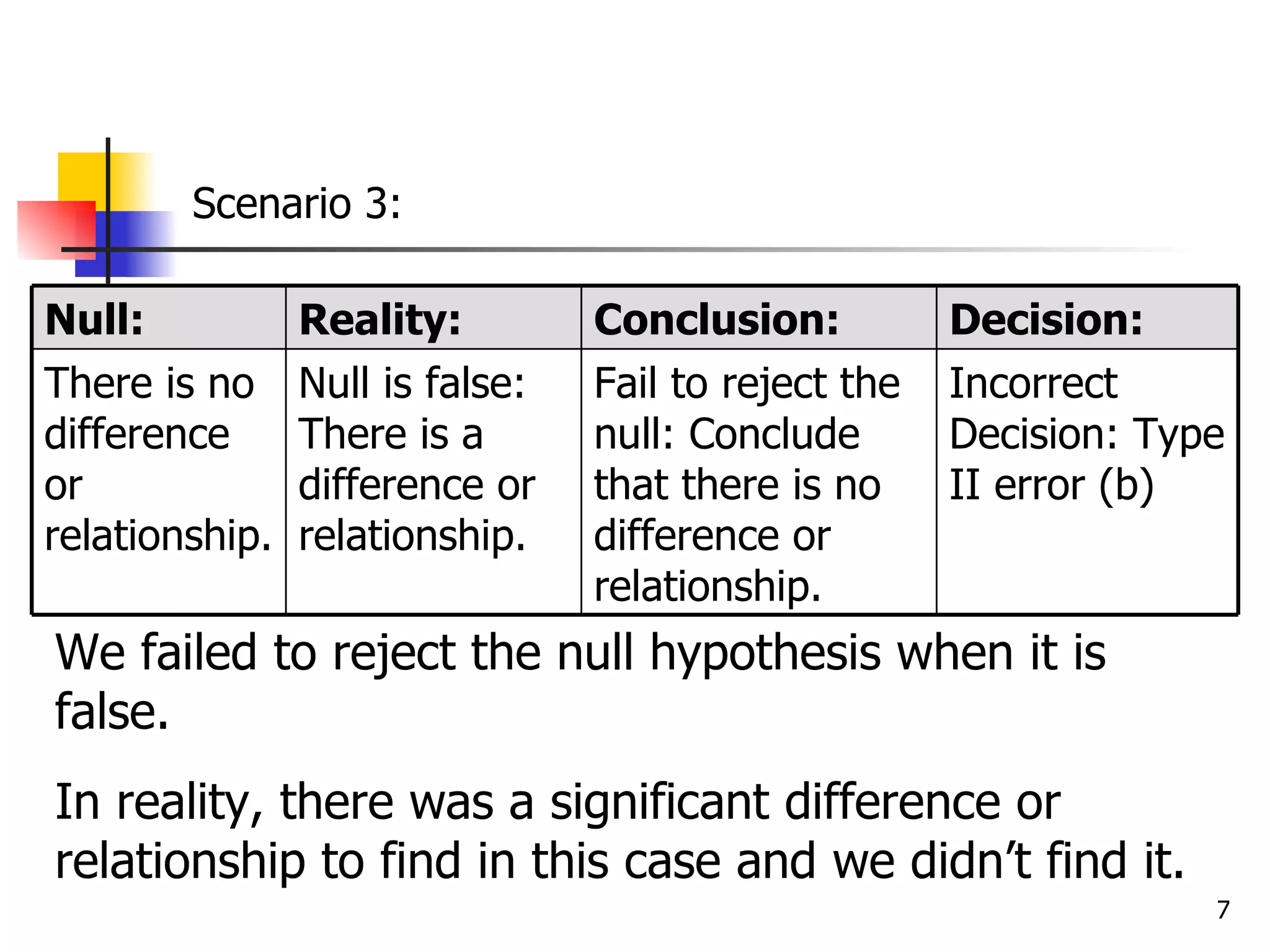
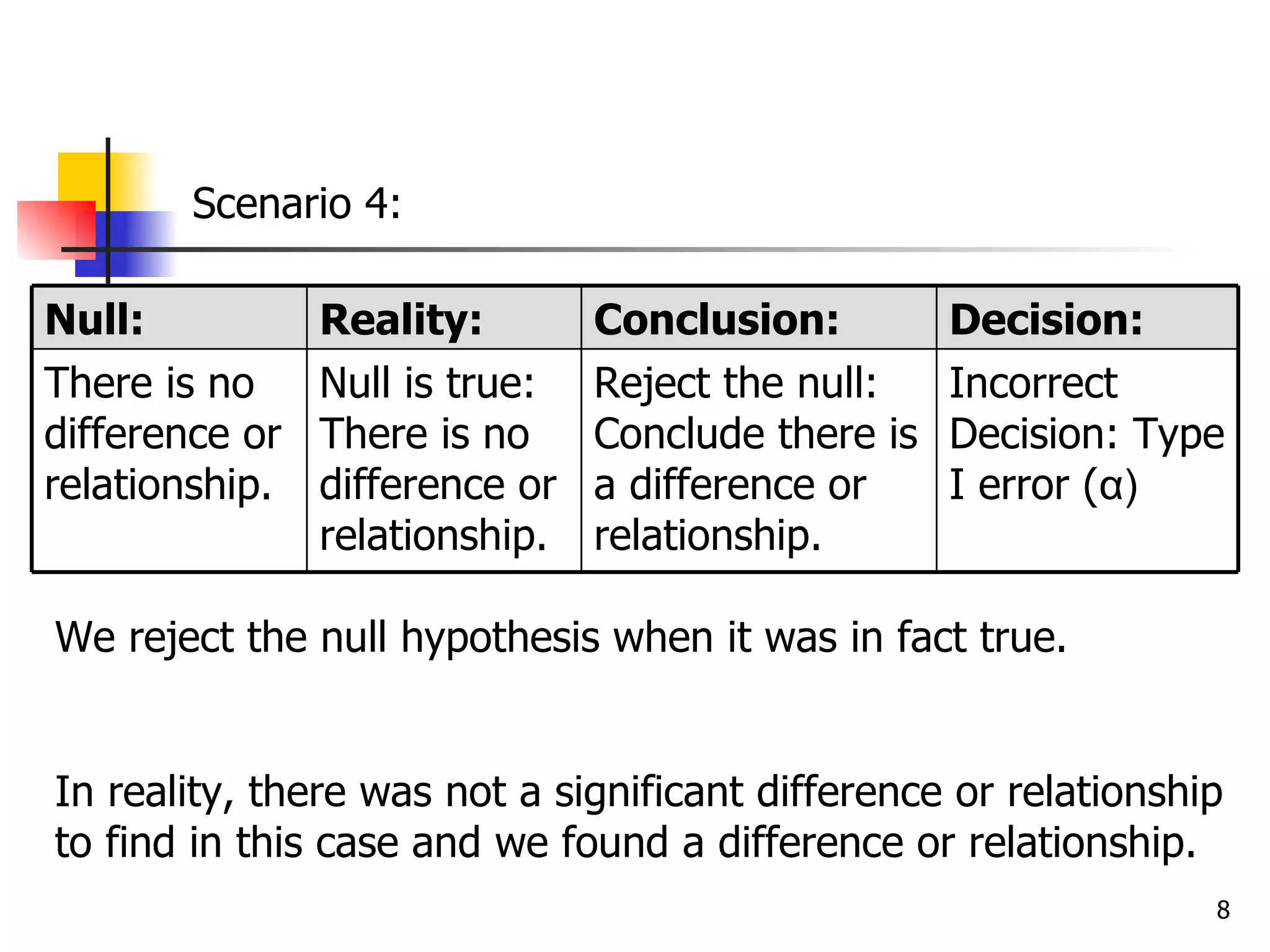
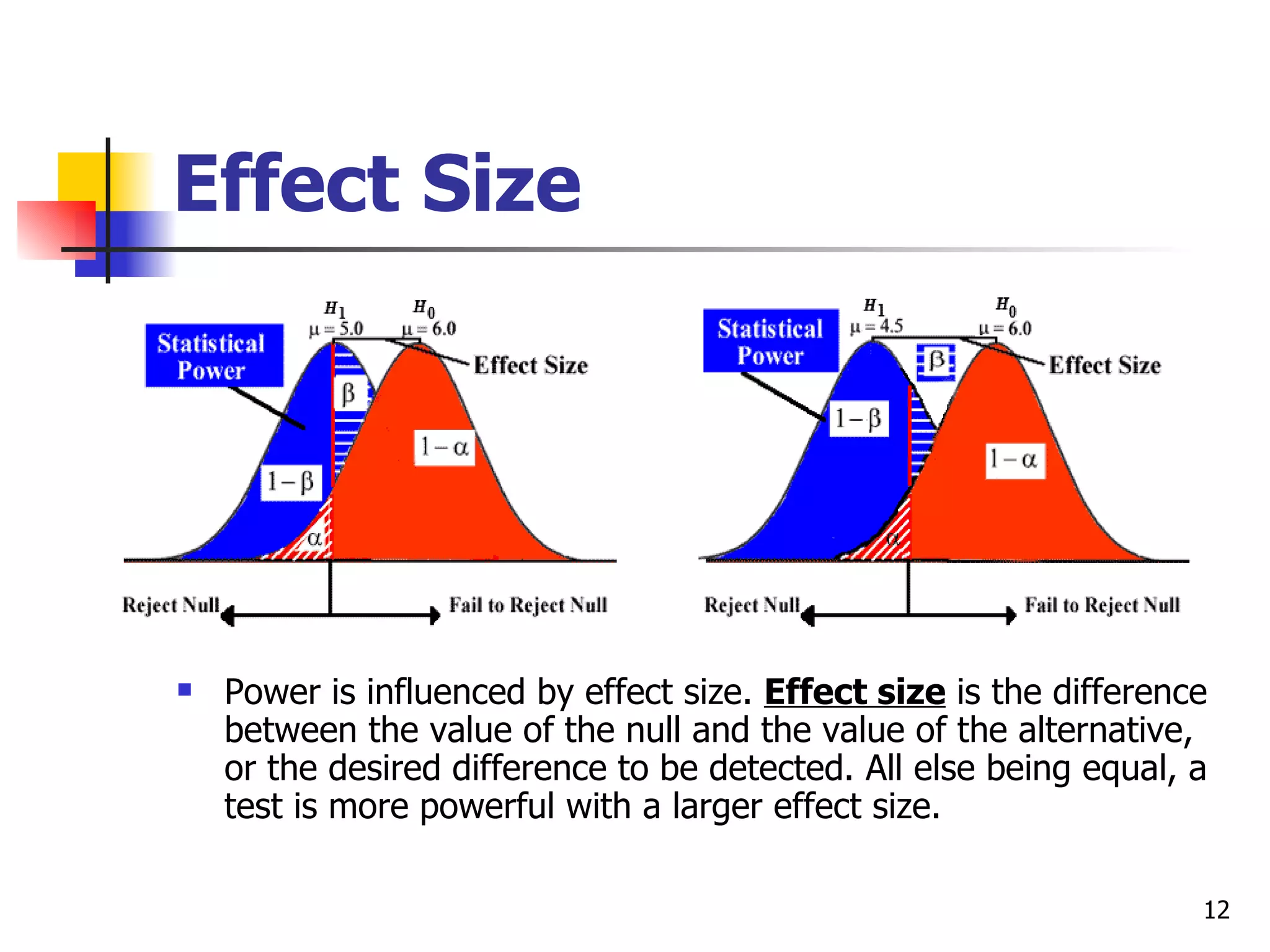
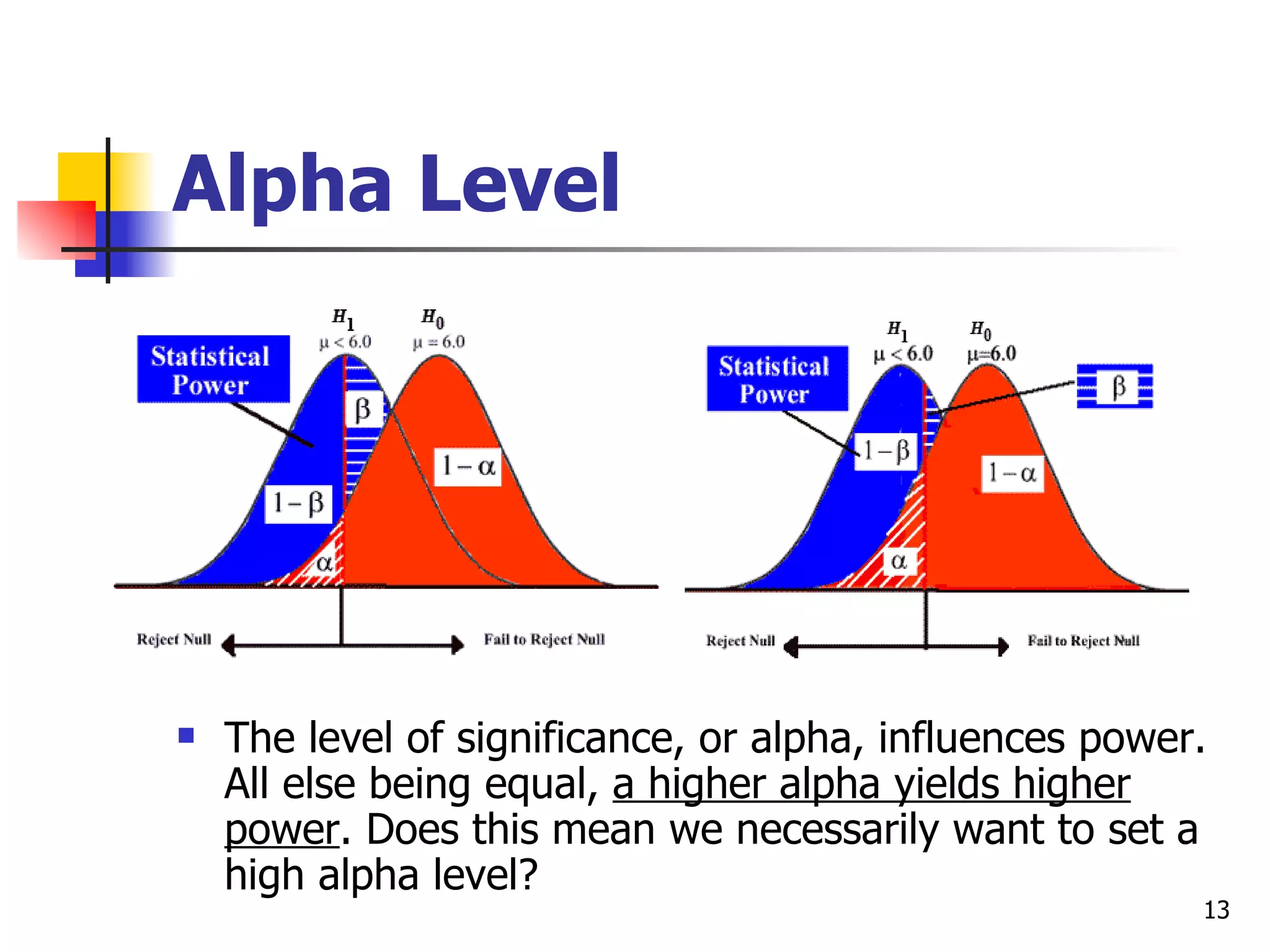
This document discusses type I and type II errors in hypothesis testing. A type I error occurs when a true null hypothesis is falsely rejected, while a type II error is the failure to reject a false null hypothesis. Statistical power is the probability of correctly rejecting a false null hypothesis. Factors that influence power are sample size, effect size, alpha level, and directionality of the test. In general, larger sample sizes, larger effect sizes, higher alpha levels, and one-tailed tests result in higher statistical power compared to their counterparts.